【模拟退火】小学六年级必学经典
进来学退火
- 扯一扯
-
- 【例题】
- 【爬山算法】
- 【真正的模拟退火】
- 模拟退火更综合也更常见的应用
-
- 【八皇后问题】
- 待会更
扯一扯
这是一篇为了让保洁阿姨学会退火而写的博客,如果你没看懂
emmmm。。。
那一定不能怪我,肯定是保洁阿姨太聪明了!

【例题】
众所周知,lwh很怕冷,现在在一个房间内,有n台空调,lwh当然想和空调们靠的更近。现在给出每台空调的坐标,求一个点,使lwh与所有空调的距离的和最小,输出最小的距离和。
这道题不用退火当然也能做,甚至用退火做也不一定能算退火,作为例题主要是为了让保洁阿姨也看懂。
#include看了代码你可能会有个问题:
while(t>t_min){
//省略
t=0.99*t;//俗称降温
}
那就是上面这串代码似乎是没有意义的,直接用一个for循环好像也能解决。这是因为这道题有个特殊点,就是更优的点只可能在更优的方向,这是什么意思呢,就是说哪怕不用模拟退火,写一个简单的贪心就可以解决了。

那么在引入退火的真正用途之前,先让我介绍介绍另一种更普通的贪心算法,在学习这种算法的同时,你一定可以看出退火的优势。
【爬山算法】
所谓爬山算法,就是一种简单的贪心算法,永远只向更优的方向走。通俗的说,就是lwh在爬一座山,她每次都往四周看看,有没有比现在高的地方,有的话她就往更高的地方走。如果她走到一个地方,四周都没有比这里更高的了,lwh就认为她来到了山顶。
想必大家在小学五年级下册的时候一定都对这种算法有了一定的了解,用这个算法解决上面那道例题并没有一点问题。
但是,我们假设lwh身处的并不是一座山脚下,而是一群山脉之间,她希望自己能爬上最高的山峰。如果她还是按简单的爬山算法,很可能在一座相对高的山顶她就停下了脚步,这样的山顶我们称之为“局部最优解”。显然,爬山算法只能寻找最近的一个局部最优解,而并不能确定这个解是全局的最优解。

【真正的模拟退火】
模拟退火相对于爬山算法的优点就在于,它并不是每一步都只会往更优的方向走,而是会以一定的概率来接受一个比较差的解。这样的话lwh就有机会走下小山峰,而登上真正最高的山顶啦!(鼓掌)
现在我们了解到,lwh在爬山的时候很喜欢看天上的星星,因为她觉得星空特别的美,美到她想用一个球把星星们装起来(好生硬),那么问题来了:现在给出n颗星星的三维坐标,求一个最小的半径,使这些星星能全部被一个球包裹起来。
下面贴上我的代码,我会根据这个代码解释解释退火的含义。
#include这次没写注释,不过我会一点一点解释的。
这个代码其实主要由几个部分组成
初始化:(这一块基本没用)
struct point{
double x;double y;double z;
}p[100000];
int n;
cin>>n;
rep(i,1,n){
cin>>p[i].x>>p[i].y>>p[i].z;
}
point a;
a.x=p[1].x;a.y=p[1].y;a.z=p[1].z;
double t=100;
double tmin=1e-14;
double ans=100000000;
“价值”函数:
double s(point a,point b){
double ans;
ans=sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
return ans;
}
其实本题中点a的价值应该是a到各点的距离中最大的那个。
退火过程:
while(t>tmin){
int flag=1;
rep(i,1,n){
if(s(a,p[i])>s(a,p[flag]))flag=i;
}
double tp=s(p[flag],a);
ans=min(ans,tp);
a.x=a.x+(p[flag].x-a.x)/tp*t;
a.y=a.y+(p[flag].y-a.y)/tp*t;
a.z=a.z+(p[flag].z-a.z)/tp*t;
t=t*0.99;
}
这个退火过程和之前那道例题其实并没有很大的区别(至少t=t*0.99是一样的)。别的语句仔细读读一定也能读懂,那么对于初学者来说,最难懂的其实就只有一句话:
a.x=a.x+(p[flag].x-a.x)/tp*t;
也就是往下走的这一步。
在解释这句话之前,我想先补充一下退火本身的意思(好像我从一开始就没有说)
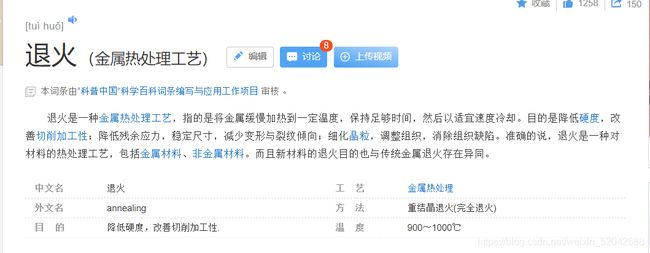
好!真不错!竟然能给出这么严谨并且美丽的定义,不愧是我!(不是)
那么物理退火和模拟退火究竟有什么共同点呢,或者说为什么这个算法要叫模拟退火呢,因为有这样一句话是相通的:
温度越高的时刻,物质(答案)的状态越不稳定。
重点呐重点,看到我加粗了吧,还不醒一醒。

其实模拟退火就是模拟了退火中降温的那个过程,温度越来越低,答案的状态也越来越稳定。此时我再来解释之前那一行代码的意义,你一定能理解的更加清晰了。
p[flag]是我们找到的离a最远的点,想要减少球的半径,很容易想到的办法就是使a向p[flag]移动,那么该如何移动、移动多少呢,这是一般的算法难以抉择的。而模拟退火则给出了一个暴力的解法,既然我无法得知该怎么走才更好,那我就接受一切的走法!(p[flag].x-a.x)给定了一个方向,使a向p[flag]移动,而除以tp则使a不至于回不来(好抽象,我也不知道咋解释),乘以t则是整个代码的关键所在。
如果你留意我的t的初值,是100,不难想象,第一遍走的时候a向p[flag]走去,却越过了p[flag],走的非常远,甚至比原本的距离还远了不少,这就是所谓温度高时的状态不稳定。而随着t=t*0.99一遍又一遍的降温,a每次的步伐也会越来越谨慎,这就是所谓的状态趋于稳定,那么在退火的过程中,温度不断降低,答案改变的可能也越来越小,最后就大概率会得到正确的答案了。
好像也没那么清晰,不过,接着看吧查帕斯!(??为什么我要喊查帕斯)
模拟退火更综合也更常见的应用
【八皇后问题】
来一道经典的题目——八皇后问题,大家以后小升初的时候很有可能遇到。问题可以表述为:在8*8的棋盘上摆放8个皇后,使任意两个皇后不能互相攻击,即任意两个皇后不能处于同一行、同一列或同一斜线上。
这个问题有好多方法可以解决,模拟退火也不能说是最好的方法,在这里我会用三种不同的爬山算法与模拟退火一起比较,来观察模拟退火的优势和劣势。
首先,我们用一行数字串来表示一个状态。比如16754283,第i个数用来表示第i行的皇后在第几列的位置。然后我们需要一个函数来表示这个状态的“价值”,在这里我用相互冲突的皇后的对数来表示,显然,相互冲突的皇后的对数越少,该状态的“价值”就越高。
所以我们可以写出这样的判断函数,这个函数在之后的每一个方法中都会使用:
int attack(int a[]){
int count=0;
for(int i=1;i<=7;i++){
for(int j=i+1;j<=8;j++){
if(a[i]==a[j])count++;
if((a[j]-a[i])==(j-i))count++;
}
}
return count;
}
最陡上升爬山法
啥叫最陡上升爬山法呢,就是在当前状态往四周找,找到一个最陡的(也就是相对最优的)一个方向,然后作为下一个状态,当四周都没有比当前状态更优的状态,那么就视作退出。显然,如果进入这样的状态而还没有实现我们八皇后问题的要求,这一次爬山就可以算作失败了。
下面看我操作。
int zhuangtai_now=attack(a[]);
for(int i=1;i<=8;i++){
//第一层循环,遍历我要改变第i行的皇后
int min_attack=zhuangtai_now+1;
int k=1;//记录第i行皇后移动的局部最优情况的列号
for(int j=1;j<=8;j++){
//第二层循环,表示我要把第i行的皇后移动到第j列的位置
a[i]=j;//移动
int zhuangtai_new=attack(a[]);
if(zhuangtai_new<min_attack){
k=j;
min_atack=zhuangtai_new;//使min_attack中存放我们需要的最优情况的价值
}
}
if(min_attack<zhuangtai_now){
//如果存在更优状态,更新状态
zhuangtai_now=min_attack;
a[i]=k;
}
else{
//跑到这里证明已经不能更新状态了,而zhuangtai_now并不等于0(因为上一轮就没退出啊),所以本次寻找以失败告终
cout<<"失败啦"<<endl;
}
if(zhuangtai_now==0){
//输出答案,即a数组,这里就不写啦
break;
}
}
首选爬山法
首选爬山法与最陡上升爬山法的区别就在于,首选爬山法找到第一个比较优的状态就进行了更新,而不是寻找到四周最优的那个状态。下面是首选爬山法的代码。
int zhuangtai_now=attack(a[]);
for(int i=1;i<=8;i++){
int flag=0;
for(int j=1;j<=8;j++){
int k=a[i];
a[i]=j;
int zhuangtai_new=attack(a[]);
if(zhuangtai_new<zhuangtai_now){
zhuangtai_now=zhuangtai_new;
flag=1;
break;
}
else a[i]=k;
}
if(flag==0){
cout<<"失败啦"<<endl;
break;
}
if(zhuangtai_now==0){
//输出答案,即a数组,这里就不写啦
break;
}
}
应该不难理解,实在不能理解就多理解理解0.0。
随机重启爬山法
随机重启爬山法其实是对爬山法的一种挽救,当我一次爬山法失败时,就随机产生一个新的初始状态,然后再次进行爬山法,当我随机重启的次数达到上限时,我才认为它真正的失败了。具体该使用最陡上升爬山法还是首选爬山法作为爬山逻辑,其实都可以,在这里我用的是最陡上升爬山法。
int sum=0;
while(sum<1000){
sum++;
int flag=0;
int zhuangtai_now=attack(a[]);
for(int i=1;i<=8;i++){
int min_attack=zhuangtai_now+1;
int k=1;
for(int j=1;j<=8;j++){
a[i]=j;
int zhuangtai_new=attack(a[]);
if(zhuangtai_new<min_attack){
k=j;
min_atack=zhuangtai_new;
}
}
if(min_attack<zhuangtai_now){
zhuangtai_now=min_attack;
a[i]=k;
}
else{
cout<<"失败啦"<<endl;
}
if(zhuangtai_now==0){
flag=1;
//输出答案,即a数组,这里就不写啦
break;
}
}
if(flag==1)break;
random_shuffle(a+1,a+9);//随机获得一个新的初始状态
}
模拟退火
上代码之前我先引入退火中最常见的一个操作:
if(((float)(rand()%1000)/1000)<exp(deltaE/t)){
更新状态
}
你看大部分退火的博客都会看到类似这样的语句,然而并没有人解释一下,也许这个是理所当然吧=v=。不过我在这里还是解释解释。这个函数具体长什么样都无所谓,最主要的是得和t正相关,并且有个rand()来随机概率,也就是t越大的时候越大,也就是t越大的时候越可能接受更差的状态改变。
没错,这句话就是写在判断状态更差之后,当我们发现了新的状态并不是更优的,不要着急否定它,来,套上这个公式,rand()一下,然后,万一就接受了呢qwq。这就是模拟退火与众不同的地方,赌狗,谁还赌不起了(其实也没有)。

虽然引用了rand()来随机概率,但是实际上概率的大小完全可以用函数来控制,所以啊,模拟退火的难点一般在这两个地方:寻找“价值”函数,寻找概率函数!
天呐,简直太清晰了,真佩服我自己。

好了好了,还是先上个代码。
懂了吧
开玩笑的,我还在写