GIoU DIoU CIoU loss 损失函数

目标检测任务中，Bounding Box的评估指标是IoU，IoU范围在$(0,1)$之间，具有尺度不变性，而且可以衡量各种形状的匹配程度。我们自然会考虑能否将IoU设计为一个损失函数。

IoU loss

最简单的，直接将1-IoU定义为损失，我自己在简单的目标检测项目中尝试过，基本没有办法学习，主要原因是：当预测框和目标框不相交时，IoU始终为0，损失函数不可导，无法优化。

另外这种损失定义方式无法区分IoU的各种情况，同样的IoU值，重叠形状可以有许多种，它们在效果上是有差异的，因此我们在损失中应该表现这种差异，如此才能获得合适的优化力度。接下来对IoU损失的改进过程，都是为了更合理地衡量预测框和目标框的差异。

GIoU loss

定义$GIoU=IoU-\frac{|C-(A\cup B)|}{|C|}$，$C$是预测框和目标框的最小外接矩形。

GIoU损失不仅关注重叠区域，还关注非重合区域，解决了无重叠框之间差距无法评估的问题。当预测框和目标框完全重叠：GIoU=IoU=1；当预测框和目标框无重叠，GIoU随着距离增大而减小，趋近于-1。

DIoU loss

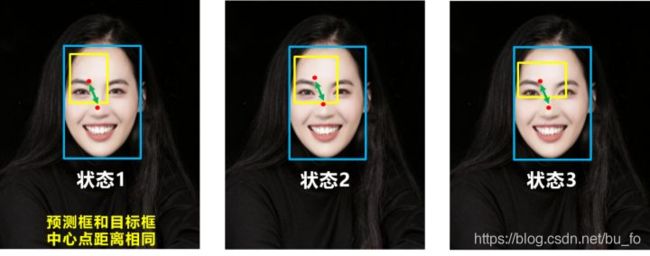
GIoU有一个问题，一旦预测框和目标框出现包含关系，或者宽和高对齐的情况，差集为0，GIoU就退化成了IoU，无法评估相对位置，收敛缓慢。

定义$DIoU=IoU-\frac{D_2^2}{D_C^2}$，$D_2$为预测框和目标框中心点距离，$D_C$为最小外接矩形$C$的对角线距离。

DIoU损失相当于在保留GIoU损失优点的基础上，增加了中心点距离度量，直接优化两个框中心距离，快速收敛，而且仅中心点完全重合的时候，才会退化成IoU。

DIoU 还可以替代普通的 IoU 评估，应用于NMS中，效果更合理。

CIoU loss

最后还有没考虑到的差异，就是形状了，也就是宽高比。

$$CIoU=IoU-\frac{D_2^2}{D_C^2}-\alpha v$$ $$\alpha =\frac{v}{(1-IoU)+v}$$ $$v=\frac{4}{{\pi }^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}{)}^2$$

CIoU的公式看起来有点复杂，但其实只是在DIoU上增加了一项$\alpha v$，$\alpha$是个平衡参数，不参与梯度计算，真正重要的就是$v$，先无视前边看似高大上的系数，直接看括号里的$arctan\frac{w}{h}$，根据咱高一学过的反三角函数，这不就是矩形对角线的倾斜角度嘛~

当预测框和目标框的宽高比相等，矩形对角线倾斜角度相等，两者形状一致。

可能有些同学还在纠结这个有点眼熟的系数$\frac{4}{{\pi }^2}$，好叭，这是因为$arctan\frac{w}{h}$，也就是矩形对角线的倾斜角度，范围在$(0,\frac{\pi }{2})$，所以$(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}{)}^2$的范围是$(0,\frac{{\pi }^2}{4})$，乘上系数的作用类似于归一化。

在YOLOv4中，选择CIoU作为损失函数，测试时使用DIoU进行NMS。