2019华为软件精英挑战杯参赛总结
本博文转载自我自己的 github 博客 ——> 半天钟的博客
前言
从初赛(3月30日)结束后到今天也过了近三分之一个四月天了,现在区域复赛正在如火如荼的进行中…
“还有2天就复赛了,好紧张!!”
“你初赛就被淘汰了,复赛和你有什么关系?”
“(ಥ_ಥ)”
是的,这篇博文是菜鸟失败后的自我总结(安慰),初赛在京津冀东北赛区排到了40 ,距离进复赛差了8名,所以晋级的大佬可以点击屏幕上方的“x”键退出这个页面了。
“失败是成功之继母,总结是成功之亲爹”
这场比赛虽然结果不尽人意,但是依旧收获了许多,接下来,文章会通过回顾我们小组在比赛过程中的历程和思路,总结一下得失。
代码仓库的情况
团队协作的竞赛,最好的协作方法自然是使用git版本控制系统了,事实上我们也是这么做的。
Github在被微软收购后,可以免费创建私有代码库了,免费代码库只能拥有最多三名协作者,这对于我们这个三人小队来讲却足够了。
在仔细看过比赛的特别声明(大赛组委会对未入围的作品没有著作权)后,我终于可以放心的将代码仓库设为public了。
源码仓库的地址戳这里 -> secretCode repo
仓库的文件结构是这样的:
mainfile
├─SDK_python
├─CodeCraft-2019
├─config
├─logs
└─src
├─CodeCraft-2019.py
├─Test.py
├─base_class.py
├─testdijkstra.py
└─tools.py
├─CodeCraft_tar.sh
└─build_and_run.sh
1-map-exam-1.zip
1-map-exam-2.zip
1-map-training-1.zip
1-map-training-2.zip
HuaweiAnswer.cpp
.
.
.
secretCode相关文件安排.md
mainfile 里的文件是比赛的主要代码,和mainfile同级的目录里存放着一些与比赛相关的文件、比如说:
- 训练赛和初赛的数据压缩包
- 地图数据可视化后的图片
- 最重要的是组里的C++大佬写的cpp原型程序(主程序中的很多想法都是从这些cpp里面借鉴的)
mainfile目录下的文件是按照比赛SDK的要求放置的,因为用的是python语言,所以根目录是SDK_python,src里的文件就是我们编写的主要程序文件了,其中:
- base_class.py 里放着所有程序相关的基本类,如路口类、道路类、地图类等实体类。
- tools.py 里放着工具类,该类有着关于读写输入文本文件,将结果输出至answer.txt、寻路算法、调度算法等主要处理数据的函数。
- testdijkstra.py是调试基于最小堆优化的迪杰斯特拉寻路算法的源文件,寻路算法后来被整合到tools里了
- Test.py 是调试将输入的地图数据转换成可视化地图(二维数组)的算法。
- CodeCraft-2019.py 是SDK规定的主程序文件。
问:为什么用python?
答:因为我不想秃头
赛题分析
赛题的介绍请看官网的介绍,因为初赛的任务书只有参赛后才能下载,所以不知道放在网上是否侵权,所以就不放在仓库了,大体的情况和上面那个连接差不多。
简单的分析一下赛题:
- 程序的输入是三个文本文件,分别是road.txt、cross.txt、car.txt
- road有如下属性:
#(道路id,道路长度,最高限速,车道数目,起始点id,终点id,是否双向) - cross有如下属性:
#(结点id,道路id,道路id,道路id,道路id) - car有如下属性:
#(id,始发地,目的地,最高速度,计划出发时间)
- road有如下属性:
- 程序需要输出一个文本文件 —— answer.txt
- . answer有如下属性:
#(carId,StartTime,RoadId...)
- . answer有如下属性:
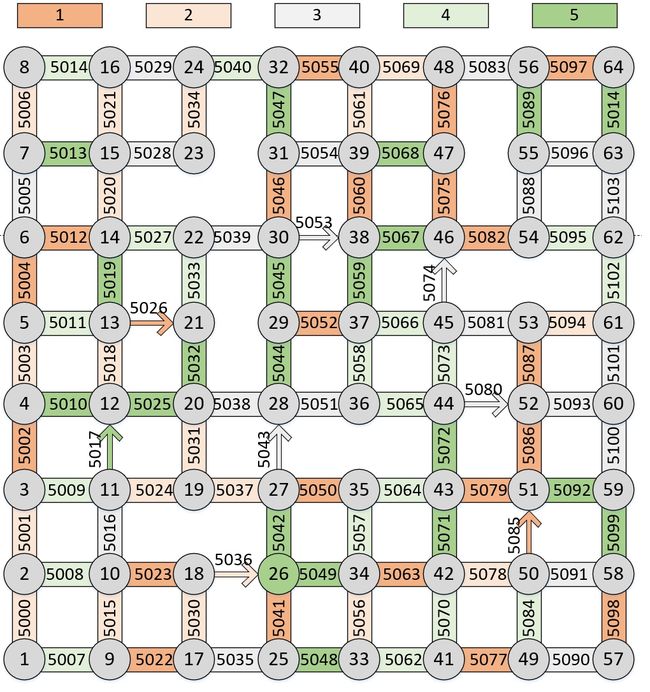
- 输入的三个文本文件中,road 和cross 的所有对象可以描绘出一个地图,例如训练赛的地图可以画成这样:
- 车辆从自己的始发地开往目的地,具体的出发时间是由我们的程序计算的(输出到answer的StartTime),但是不能早于car的plantime(计划出发时间)
- 赛题还规定了多辆车一起运行时的一系列约束条件,比如*不允许超车变道、排队先到先行*等。
- 因为有着一系列的约束条件、所以当很多车辆(初赛要跑1W辆车)一起运行时,容易发生死锁问题 -> 车道塞满了,你过不来,我过不去。
其实不难得出、我们的程序主要有两个部分的难题:
- 让每辆车找到从起点到终点的路。
- 找到一种方法设定每辆车的优先级,在**不发生死锁** 的前提下,让调度时间尽可能的短。
解题思路与方案迭代
在解决那两个部分的难题之前,我们需要先考虑一下整个程序的结构。
经验告诉我,磨刀不误砍柴工,虽然这个刀磨得也不锋利
首先程序至少有四个实体类——road、cross、car、answer,这几个实体类需要放在一个模块里以供调用,所以我们设置了base_class.py。
因为要输入和输出文本文件,所以至少要有一个工具类专门处理这些事情,所以我们设置了tools.py。
因为要寻路所以需要有一个地图类去处理每一辆车的寻路问题,所以我们设置了基础类-RoadCrossMap,详细的代码请看base_class.py,这个RoadCrossMap会处理所有和地图构建相关事情,拥有的方法也都是和寻路和构建地图相关的。
这是我们最初的想法,也就这样草草的分配了需要的类和函数,根目录的secretCode相关文件安排.md记录了这些想法。
然后就是解决核心的两个问题了
寻路算法的选择
首先是寻路算法的选择、这部分我们查了一些资料、问过一些大佬、也商量了一段日子,我们考虑过这几种寻路算法:
- 最短路算法
- Dijkstra算法
- Bellman-Ford算法
- Floyd算法
- SPFA算法
- 智能调度算法
- 蚁群调度算法
- 转化为一笔画问题
在最短路算法是相对容易实现的、我们可以将车在道路上的理论最快行驶时间当做图中边的权值。
蚁群调度算法和一笔画问题计算路径的时间复杂度会远高于最短路算法,性能会怎样是未知的。
这个时候我打算遵循构建机器学习项目的关键思想:
不拘泥于细节、先用最简单的方法实现、实现后如果发现这是问题导致了性能瓶颈、并且改善它能提高很多的性能(性价比高),那么再花时间想办法改善它。
这个构建机器学习项目的关键思想不是我说的,是吴恩达老师在他的深度学习教学视频中明确提到的,如果感兴趣可以去Coursera的deep-learning页面申请助学金,我很推荐这个课程,它让我获益良多。
吴恩达老师在该专项课程中的课程3-Structuring Machine Learning Projects中有明确提到这个思想。
这种思想对于学术研究来讲也是通用的,这是我有幸听到西湖大学的校长施一公先生的演讲后得到的宝贵经验。
于是寻路算法的选择便转化成了怎么挑选最短路算法的问题了,在重新审视了这几个算法的时间复杂度、和稳定性以后、我最终选择了基于最小堆优化过后的Dijkstra算法。
理论上来说基于最小堆优化过后的Dijkstra算法在图点数为V、边数为E的图中时间复杂度为V * O(logE) ~ V * O(logV)
接下来是这个最短路的实现代码,你可以在tools.py中找到它:
#dijkstra算法,获取单源点到多终点的最短路,并返回最短路字典
def dijkstra_raw(self,edges, from_node, to_node_list):
"""
:param edges: 边集 ——(路头,路尾,权值)
:param from_node:源点
:param to_node_list:终点列表
:return: shortest_path_dict:最短路的字典 {key = to_node : value = (cost,path)}
"""
shortest_path_dict = {
}
g = defaultdict(list) # 定义一个空字典、此字典若没找到key,则返回空列表[]
for l, r, c in edges: # l:源点、r:终点 c:距离
g[l].append((c, r)) # 建立一个字典,元素是源点为key、(距离,终点)为value
q, seen = [(0, from_node, ())], set() # 初始化优先队列、初始化已找到的最短路径集合——————元组(源点到点A的距离,某个点A,源点到点A的路径)
while q: # 优先队列为空时,循环结束
(cost, v1, path) = heappop(q) # 从优先队列中找出与源点距离最小的点
if v1 not in seen: # 若点v1以确定最短路径则无需计算
seen.add(v1)
path = (v1, path)
if v1 in to_node_list: # 如果找到了某一个终点
shortest_path_dict[v1] = (cost, path)
if len(shortest_path_dict) == len(to_node_list): # 如果所有的tonode都找到了
return shortest_path_dict
for c, v2 in g.get(v1, ()): # 更新优先队列,加入与当前点相连的所有点的信息
if v2 not in seen:
heappush(q, (cost + c, v2, path))
return {
"ERROR": (float("inf"), [])}
你希望我一行一行的给你解释?这不可能,因为我自己都快忘了是怎么写的了…
你可能注意到了:
- 解决单源点最短路问题的Dijkstra算法本来可以找到到所有点的最短路的,可是为什么要设定了一个终点列表
- 因为当找到了终点列表中的终点的最短路,循环就就结束了,这增加了寻路的速度。
- 为什么返回的最短路径是嵌套的元组,这样想得到最短路列表还得去一层层的剥开它的心?
- 因为我喜欢杨宗纬的《洋葱》(倔强脸)好吧,是我懒了,可以改善它。
- 地图的表示不是一个二维数组、而是使用边集表示
- 使用边集就可以算出最短路径了,这意味着我们只使用road对象列表就能得到最短路径、而不用去读cross对象列表。
- 地图的二维数组不太好得到,说实话我们最后也没有写出一个鲁棒性很强的算法来得到二维数组、这是我们失败的原因之一。
- tools.py后面还有一个dijkstra方法是什么?
- 那是用于计算所有answer对象的,因为我不知道取什么名字好了。
调度算法方案迭代
这是最关键的核心问题了,许多的队伍都是因为不知道如何设置车辆的starttime而频繁的发生死锁问题,这在官方论坛中很常见。
我们在这个算法方案上迭代了5次、每次迭代都会复杂一点。
方案一
如下图:
这应该是最简单、效率也最低的方案了,每辆车的出发时间是前面所有车行驶时间的综合、行驶时间是最短路 / 理论最高速。
这其实不算方案,算是我们测试程序的其他模块是否正确的黑盒测试,让我们确保了除了调度算法以外,其他的模块都运行正常。
方案二
比方案一进步了一点点、我们一个路口、一个路口的跑…
有如下规则:
- 在同一个路口出发的车,最高速度越快、越先调度
- 如果A车和B车出发路口一致、且最高速一致、那么他们的出发时间一致、但是判题器会优先调度id更小的车。
- 哪个路口先跑?
- 这个问题方案二没有仔细的考虑
如果你仔细阅读了源码,你会发现,在tools.py中的classify_of_diff_ori_car方法返回的字典中,路口的顺序是怎样的,那么路口优先级的顺序就是怎样的,这让本方案的路口优先级似乎又有规律可循,不过当时没有仔细的思考这个问题,因为我们从不认为这是我们的最终方案。
说出来你可能不信,除了增加了一些细节以外,这个方案就是我们初赛的最终方案。
这不是后面的方案不行,而是因为一些其他的问题,这在最后总结中会给出详细的说明。
方案三
方案三又比方案二进步了一点点、因为我们手动为每一个路口设定优先级了。
除了路口优先级的设定、前两个规则和方案二没有区别。
路口优先级是这样设定的:
首先、我们默认由road、cross文件生成的地图都是方形、这是由官网的介绍中的路口数据文件描述推理得到的、但是有可能在方形地图的中间会有一些缺失的路口。
那么地图的数据就可以转换成一个二维矩阵了、不管实际的地图是长方形还是正方形。
优先级规则:
- 规定方形地图由外到里优先级逐渐减低
- 为了方便制定规则3、我们定义了层级的概念、即以方阵中心点画同心圆(椭圆)、能被同样的两个圆(椭圆)夹住的路口属于同一层级。
- 每一层级中两个理论距离最远的两个路口一起发车!
- 每一层级的路口按照顺时针的顺序,优先级降低。
解释:
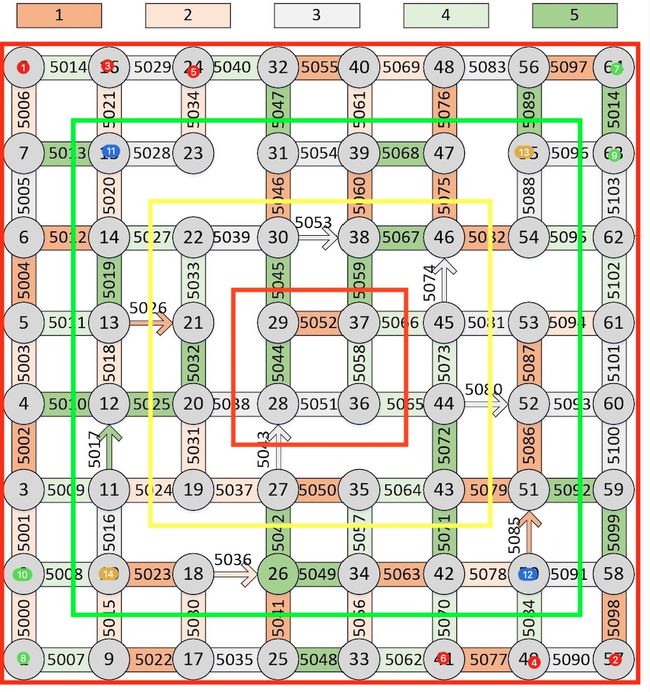
上图被红色框框和绿色框框夹住的路口(下面简称层级一)优先级最高、绿色框框和黄色框框夹住的路口(下边简称层级二)优先级次之。
在层级一中、红色标注1路口和红色标注2路口是一同发车的。
过了一个同层级延迟以后、红色标注3的路口和红色标注4的路口再一同发车。
以此推类、层级一中的绿色标注7和绿色标注8也是一同发车。
当第一层级的路口全都发完车以后、过了一个层间延迟以后、第二层级的车就可以发车了、例如蓝色标注11和蓝色标注12是层级二中最早一同发车的。
可以注意到、有两个参数需要调试:
1. 同层级延迟
2. 层间延迟
经过调试后、这个方案比方案二并没有快多少,这有可能是两个路口一起跑还是大大的增加了死锁的概率,经过我们的分析后得到了方案四。
方案四
你应该注意到了,方案三那个图中、红色标注3的路口(后面简称路口3)离红色标注1的路口(后面简称路口1)很近、但是路口3只比路口1晚发车了一个同层级延迟
同样的,图中id为7的路口(后面简称路口11)、和蓝色标注11(后面简称路口11)很近、但是路口11只比路口7晚发车了一个层间延迟
同样这种情况在地图中的很多相邻路口之间都发生着
有着上述情况的相邻路口、他们之间的车道会变得相当拥挤、发生死锁的概率大大的提高了!
所以方案四很大程度上避免了这种情况的发生。
优先级规则的前两条和方案三一致,只是同一层级的优先级设置规则改变了
- 现在我们每一次只发一个路口的车了。
- 依旧按顺时针确定优先级。
- 每一个路口的优先级确定以后,与之对应的三个路口的优先级也确定了
- (描述不来了,还是看图说话吧)
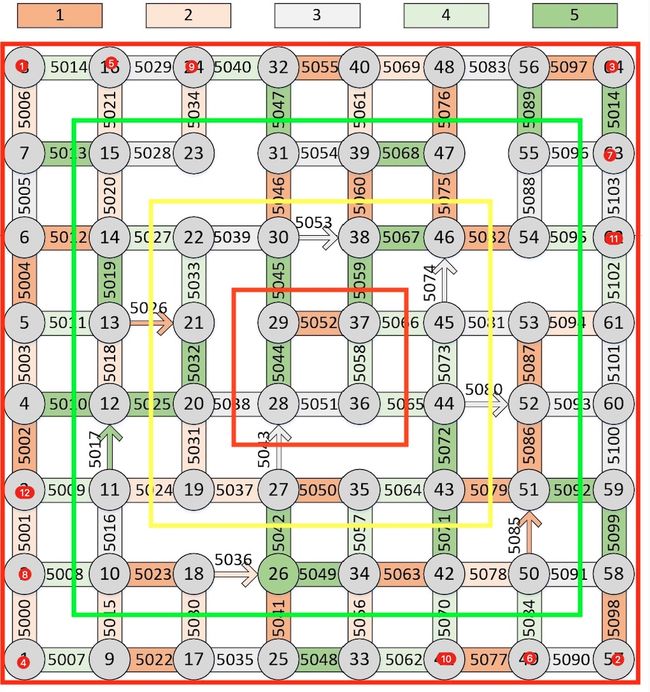
上图用红色标注、标注了12个路口、他们就是按照这个顺序发车的。
下面说的路口x,指的是标记为x的路口
当路口1的有优先级确定以后、然后确定优先级的是路口2、路口3、路口4、他们之间各自推迟了一个同层级延迟。
随后确定的是路口5的优先级、然后依次是路口6、路口7、路口8
…以此推类…
基本上是左上角、右下角、右上角、左下角的顺序(先这么概括吧、想不到如何准确描述了)
这样的优先级设置能够延缓方案三带来的高概率死锁问题。
实际上、方案四比方案三快了三分之一。
方案五
我们用方案四在当时的京津冀赛区排到了第15名。
然而,我们在路口优先级设置的相关的上已经黔驴技穷了
终于我们想到了研究地图数据(结合road数据、cross数据和car数据)、根据地图的规律来改进我们的方案。
这本应该在最开始就做的步骤却被我们拖到了现在、这对学过机器学习方法和深度学习方法的我们是很不应该的。
研究训练赛的数据以后,我们得到了如下几条规律
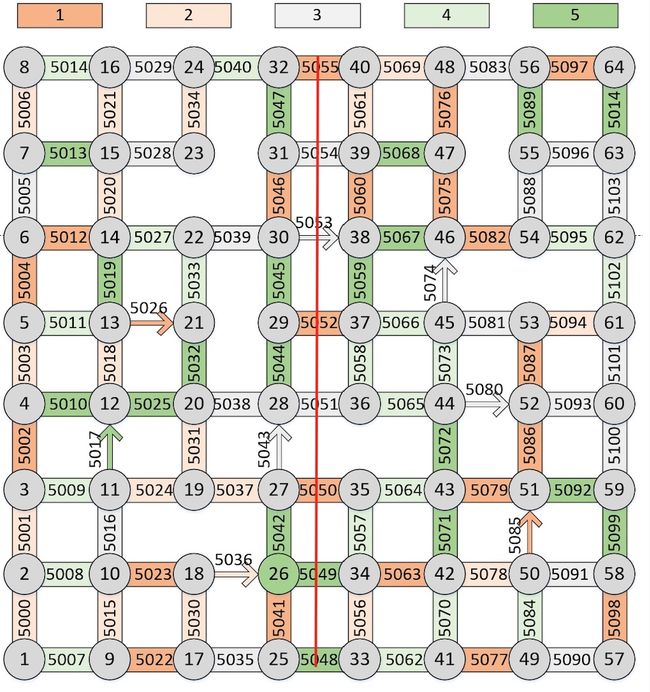
先放图:
以中间那条红色的中轴线分分割,左边的路口发的车,目的地总是在右边。
具体的规律是:
- 从路口1发车的车目的地是33路口-64路口、从路口2发车的车目的地是34路口-64路口、从路口3发车的车目的地是35路口-64路口…
- 每次都会减少一个目的路口
- 出发路口和对应的最小id的目的路口位置总是对应、如路口1对应路口33、路口2对应路口34…
- 左边的路口做出发路口时、也有类似的规律,只不过是镜像版
这样来讲、左边几乎所有的路口发出的车、都必定有车到路口64;右边几乎所有的路口发出的车、都必定有车到路口1。
综合以上所有规律、我们发现之前的方案设置的优先级方案很蠢。
所以我们打算从目的地路口入手计算每个路口的优先级。
因为时间问题、我们只写了一个简单版本的、因为过于简单我就不解释了、你可以去tools.py中的方案五的注释下查看源码。
其实是更改后效率没有提升太多、我不想写了
寻路算法的优化-最后的挣扎
因为时间的关系、我们最后没有选择继续优化路口优先级算法、而是选择了优化寻路算法
“一笔画”寻路算法的可行性讨论:
一笔画算法从理论上来讲是不会发生死锁的
因为一笔画算法在地图上画了一个环、这个环经过了所有的路口。
所以我们只要定下一个固定的方向(顺时针/逆时针)、那么所有的车都在这个环上按照一个方向行驶、
同一个地点的所有车、他们的方向一致、这就避免了死锁问题。
但是有如下弊端:
- 有些车需要绕很远的路才能到达终点。
- 同一条路上的车太多了、这会使得单车道的路极其的拥挤
所以,这个算法的瓶颈在于图中有多条单车道的道路
如果去掉所有单车道的道路、那么就不一定能画出一个能够经过所有路口的环了、这也是我们放弃了一笔画算法的原因。
有没有可能再次优化最短路算法呢?
答案是肯定的,研究了Dijkstra生成的最短路后,我发现一个情况,见下图:
![]()
前提:
- 图片最上方的带颜色的方块代表相应颜色道路的车道数、如,红色道路的车道数为1
从路口44到路口53有两种方式:
1. 44 -> 52 -> 53 (红色路线)
2. 44 -> 45 -> 53 (绿色路线)
Dijkstra算法得到的是红色的路线、可以看到他经过了5087道路、这是一个车道数为1的道路。
而绿色的路线经过了5073道路,这是一个车道数为4的道路。
经过计算、我们发现绿色路线比红色路线长不了很多、但是因为车道数较多,所以更不容易发生拥堵、也就更容易预防死锁问题。
所以我们基于这个规律再次修改了最短路上的权值、增加了车道数的因素、车道数越多的道路权值比同样长的车道数少的道路要低一些。
具体低多少根据参数决定
这就很大程度的缓解了因为车道数少而引发的拥堵问题。
至此,我说完了我们的所有解决方案 + 优化
总结
感谢你看到这里!因为太长,我自己都看不下去了
初赛的突发情况
正式初赛的那一天、在见到初赛数据的那一瞬间,我们傻眼了。
因为路口文件中的路口ID是随机的!!!!
这意味着我们生成路口位置矩阵的方法失效了,因为训练赛的数据都是按照一定规律排列的。
如果没有路口位置矩阵,那么我们只能使用效率很低的方案二了,然而这不能够确保我们晋级。
事实上,我们根据现有情况紧急写了新的生成路口位置矩阵函数(见tools.py的compute_cross_location_matrix函数)
但是,到最后这个函数也没有调试完成,只完成了函数的主体。
我保证,如果完成它,我们还是有希望晋级的。
到现在我也没去完善它,没有必要了
比赛中存在的问题
- 分工的方法不合理
上文提到的分配任务的记录文档——secretCode相关文件安排.md,只有一个版本、后来没有修改它。
并且其中没有定义数据接口、例如每个函数的输入、输出的数据格式。
后来需要分工的函数都是口头交流+代码注释实现的。
没有事先定义好数据接口让我们浪费了很多时间 - 没有事先研究数据
这是一个致命错误、如果事先研究了数据,我们可能可以直接迭代到方案五。
没有事先研究数据,走向了错误的方向,这浪费了我们很多的时间。 - 对程序的鲁棒性不够重视
比如说、如果我们一开始就以路口id是随机的来构造我们的compute_cross_location_matrix函数,那么结果很可能会不同。
收获
- 遇到复杂的问题,不要害怕,去想办法把它分解成小问题,然后依次解决。
- 就像我们把比赛的复杂问题分解成了两部分、然后依次解决了他们。
- 无论何时,都要重视算法的鲁棒性,让算法足够健壮从而能够处理意外情况。
- 不够重视算法的鲁棒性让我们吃了大亏
- 只要是数据驱动的问题、就要提前研究数据,根据数据特点定制解决方案,不管这个问题是不是打算用机器学习的方法解决。
- 要重视团队协作的法则
- 需要在一开始就商定好一个能用的方案(最初的方案),这样能够确保所有人对问题的理解一致。
- 针对最初的方案尽可能的制定好需要编写的所有模块及函数,这样能够提高效率。
- 定义好所有模块及函数的作用及数据接口的样子,并保证所有人理解一致,这能避免因为理解不同而浪费时间。