图像处理学习笔记之——Matlab数字图像处理

Matlab 数字图像处理

1、Matlab R2017b 简介

1.1、Matlab 软件环境

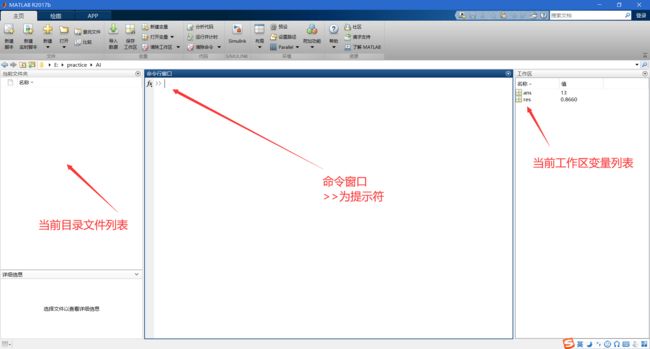
1.1.1、软件界面

1.1.2、Matlab 命令与程序

可以在 >> 提示符后面输入简单的算式，如 5*3-2；或带有函数的算式，如 sin(pi/2)*sqrt(3)/2：

>> 5*3-2

ans =

    13

>> sin(pi/2)*sqrt(3)/2

ans =

    0.8660

这样的输入形式实际上是 Matlab 命令，而如果在每行命令的结尾输入半角分号，命令窗口不会立即显示命令执行结果，而会将结果保存到工作区中。如下：

新建文件，从而来创建一个 Matlab 程序。在 Matlab 程序中，使用 % 表示注释。

1.1.3、跨行语句

Matlab 还允许将同一条语句分割在多行中书写以方便较长语句的阅读，方法是在行末使用 3 个半角圆点。如：

>> z = 2 .* x + exp(x .^ 2 + y .^ 2 - sqrt( 1 - log (x) - loy (y) ) ) ...
		-y .* sqrt(t) - x .* sqrt(t);

1.2、文件操作

默认情况下，Matlab 可以自动搜索到当前目录和 Matlab 的路径变量 path 中所含目录下面的文件。对处在这些位置可由 Matlab 执行的文件，直接在命令窗口中键入文件名即可运行。如果需要直接运行其他目录下的文件，就要使用 addpath 和 genpath 等命令向路径列表中添加路径。

1.2.1、addpath 函数

addpath 函数向 path 变量中加入指定的目录路径，其原型如下：

addpath('dir','dir2','dir3'...'-flag')

该函数可接受任意数目的参数。

参数说明：

• dir、dir2、dir3 等为要加入的目录路径，这些变量必须是绝对路径；

• flag 参数可以用来指定函数的行为，它是可选参数，其取值的含义如下：

  合法取值	含义
  0 或者 begin	这些路径将被添加到搜索列表的最前面，这些目录中的文件将先于原列表中的同名文件被找到从而执行（优先执行）。往往用于需要修改系统某一命令行为的场合
  1 或者 end	这些路径将被添加到搜索列表的最后面，这样可避免用户 M 文件覆盖系统 M 文件
  省略	同 0

1.2.2、genpath 函数

genpath 函数生成包含指定目录下所有子目录的路径变量，其原型如下：

p = genpath('directory');

参数说明：

• 参数 directory 为指定的目录。

返回值

• 函数返回包含指定目录本身和其全部子目录的数据。返回值可以直接提供给 addpath，从而直接添加了一个目录及其全部子目录到当前路径列表中。通过这样的方式可以方便地调用我们自己的程序工具箱。

1.2.3、打开与编辑 M 文件

如果需要编辑某 M 文件，就可以使用 open 命令和 edit 命令，它们的调用形式如下：

open filename
edit filename

1.3、在线帮助的使用

1. help 命令

   用于查看 Matlab 系统或 M 文件内置的在线帮助信息。命令格式如下：

   help command-name
   

2. doc 命令

   用于查看命令或函数的 HTML 帮助，在浏览器中打开：

   doc function-name
   

3. lookfor 命令

   当忘记命令或函数的完整拼写时，可以使用 lookfor 命令查找当前目录和自动搜索列表下所有名字当中含有所查内容的函数或命令。其调用格式如下：

   lookfor keyword
   

4. F1 命令打开帮助浏览器

1.4、变量的使用

使用前一定要赋值，无须事先定义。变量的命名大小写敏感。

1.4.1、变量的赋值

赋值使用 “=”，变量定义时不需要显示地指明类型。默认对数字的存储类型为 double 型或 double 型数组，而字符的存储类型为 char 型，字符串的存储类型为 char 型数组。

对于字符串赋值，需要用半角单引号 ‘’ 括起来。

1.4.2、内部变量

自定义变量不要与这些变量同名。

特殊变量	说明
ans	默认的结果输出变量
pi	圆周率
Inf 或 inf	无穷大值，如 1/0
i 和 j	单位虚数值
eps	浮点运算的相对精度
realmax	最大的正浮点数
realmin	最小的正浮点数
NaN 或 nan	不定量，如 0/0
nargin	函数输入参数个数
nargout	函数输出参数个数
lasterr	最近的错误信息
lastwarning	最近的警告信息
computer	计算机类型
version	Matlab 版本

1.4.3、查看工作区中的变量

使用 who 和 whos 命令可以查看所有当前工作区中变量的情况。使用 clear 或 clear all 命令可以清除工作区中所有的变量定义，也可以在 clear 后面加上变量名清除特定的变量定义。另外，clc 命令可以用来清屏，所以这两个命令常常用在 M 文件的开头用来构造一个干净的工作区。

>> a = 1; %定义一个数值型变量 a
>> str = 'hello'; %定义了一个字符串变量（字符数组）
>> v = [3 2 1] %定义了一个数值型向量

v =

     3     2     1

>> whos
  Name      Size            Bytes  Class     Attributes

  a         1x1                 8  double              
  ans       1x1                 8  double              
  res       1x1                 8  double              
  str       1x5                10  char                
  v         1x3                24  double              

>> clear all
>> whos
>>

1.4.4、数据类型及其转换

Matlab 中的数据类型列表如下：

数据类型	说明
double	默认的数据类型，双精度方式存储的浮点数。8 字节
uint8	8 位无符号整数，范围是 0 ~ 255。1 字节
uint16	16 位无符号整数，范围是 0 ~ 65535。2 字节
uint32	32 位无符号整数。 4 字节
Uint64	64 位无符号整数。 8 字节
int8	8 位有符号整数，范围是 -128 ~ 127。1 字节
int16	16 位有符号整数，范围是 -32768 ~ 32767。2 字节
int32	32 位有符号整数。4 字节
int64	64 位有符号整数。8 字节
single	单精度浮点数。4 字节
char	字符型变量。2 字节
logical	布尔型变量。1 字节

数据的强制类型转换：

 Destination_Var = type_name(Source_Var)

其中，type_name 即数据的存储类型，Destination_Var 和 Source_Var 分别是目标变量和原始变量。例如，将 double 原始变量 a 转换成 unit8 变量 b：

>> a = 1;
>> b = uint8(a);

1.4.5、读取与保存工作区中的变量

save 可以将当前工作区的变量以二进制的方式保存到扩展名为 MAT 的文件中；load 命令可以读取这样的文件。它们的调用格式如下：

save filename arg1 arg2 arg3,...
load filename arg1 arg2 arg3,...

• filename 参数指定保存或读取变量所使用的文件名。如果不指定文件名，默认使用的文件是 Matlab.MAT；
• arg1、arg2、arg3 等参数是需要从文件中存储或读取的变量名。这两个命令分别可以存储读取一个或一组变量。

下面将 price、age 和 number 三个变量保存到文件 MyData.mat 文件中：

>> save('MyData.mat','price','age','number')

1.5、矩阵的使用

1.5.1、矩阵的定义

可以使用半角分号分隔行与行，使用半角逗号（或者空格）分隔列与列来直接定义矩阵。

>> A = [1,2,3;4,5,6;7,8,9]

A =

     1     2     3
     4     5     6
     7     8     9

还有一种方式可以生成行向量，[begin:inc:end] 会生成从 begin 开始到 end 结束，增量为 incre 的一系列数字组成的向量。

>> v = [2:1:10]

v =

     2     3     4     5     6     7     8     9    10

如果间隔为 1，也可以忽略中间的参数，直接输入 I = [2:10] 即可。

1.5.2、生成特殊的矩阵

除了直接定义外，还可以通过函数生成特定的矩阵，例如 eye(n) 生成 N 阶单位阵，zeros(n) 生成 N 阶每个元素均为 0 的方阵，magic(n) 生成 N 阶幻方阵。

函数名称	用途
eye	产生单位矩阵
zeros	产生全部元素为 0 的矩阵
ones	产生全部元素为 1 的矩阵
true	产生全部元素为真的逻辑矩阵
false	产生全部元素为假的逻辑矩阵
rand	产生均匀分布随机矩阵
randn	产生正态分布随机矩阵
randperm	产生随机排列
Linspace	产生线性等分的矩阵
Logspace	产生对数等分向量
Company	产生伴随矩阵
Hadamarb	产生 Hadamarb 矩阵
Magic	产生幻方矩阵
Hilb	产生 Hilbert 矩阵
Invhilb	产生逆 Hilbert 矩阵

1.5.3、获得矩阵大小和维度

size 函数可以获得指定数组某一维的大小，可以用来查看图像的高度和宽度以及动态图像的帧数等。其调用方法如下：

size(A,dim)

• A 为需要查看大小的数组；
• dim 为指定的要查看的维数，这是一个可选参数，若不指定此参数，返回值为一个包含数组从第一维到最后一维大小的数组。

例如，对于一个 3 行 5 列的矩阵 B，有 size(B,1) = 3，size(B,2) = 5，size(B) = [3 5]。

函数 ndims 可以查看数组的维数，调用方式如下：

ndims(A)

其中 A 为需要查看维数的数组。

1.5.4、访问矩阵元素

访问矩阵的一个元素的方式是在矩阵名字后边注明行列序号，例如访问 A 的第三行第二列元素就是 A(3,2)。提取矩阵的一整行元素，如要提取 A 的第二行使用 A(2:)，而 A(: ) 表示将矩阵按列存储得到一个长列向量。如下：

>> A = [1, 2, 3; 4, 5, 6; 7, 8,9]; %定义矩阵 A
>> A(1, :) %提取第 1 行

ans =

     1     2     3

>> A(:, 3) %提取第 3 行

ans =

     3
     6
     9

>> A(:)'

ans =

     1     4     7     2     5     8     3     6     9

对于矩阵 A，提取矩阵元素或子块的方法如表：

命令片段	用途
A(m,n)	提取 m 行 n 列位置的一个元素
A(:,n)	提出第 n 列
A(m,:)	提出第 m 行
A(m1:m2,n1:n2)	提出 m1 到 m2 行，n1 到 n2 列的一个子块
A(m:end,n)	提出 m 行到最后一行，第 n 列的一个子块
A(: )	将矩阵按列存储得到一个长列向量

1.5.5、进行矩阵运算

运算	符号	对应函数	说明
加	+	plus(A,B)
减	-	minus(A,B)
乘	*	mtimes(A,B)	通常意义上的矩阵乘法
点乘	.*	times(A,B)	矩阵的对应元素相乘。参与运算的两个矩阵必须拥有同样的大小
乘方	.^	mpower(A,B)	对矩阵的每一个元素进行指定幂次的乘方
矩阵乘方	^	power(A,B)
矩阵左除	\	mldevide(A,B)	左除 A\B 相当于 inv(A) * B
矩阵右除	/	mrdevide(A,B)	右除 A/B 相当于 B * inv(A)
左除	.\	ldevide(A,B)	矩阵中对应位置的元素的左除
右除	./	rdevide(A,B)	矩阵中对应位置的元素的右除
矩阵与向量转置	.’	transpose(A,B)	这里的转置不对复数进行共轭操作
复数矩阵转置（共轭）	‘	ctranspose(A,B)	应用于复数数值时的含义是取共轭，应用于实数矩阵时的含义与普通转置相同，应用于复数矩阵时首先对所有元素取共轭再求矩阵转置

1.5.6、细胞数组和结构体

1. 细胞数组

   细胞数组是 Matlab 特有的一种数据结构，它的各个元素可以是不同的数据结构。细胞数组可采用下标访问。

   定义一个细胞数组：

   >> Cell = {'Harry', 15, [1 0; 15 2]};
   

   也可以通过 {} 加上索引来直接定义细胞数组的某个元素，如下：

   >> %定义数胞数组的另一种形式
   >> Cell{1} = 'Harry';
   >> Cell{2} = 15;
   >> Cell{3} = [1 0; 15 2];
   

   注意使用花括号 {} 而不是方括号 [] 来定义细胞数组。对细胞数组的访问方式也很简单，同样使用花括号 {} 来给定索引值。

   >> %访问细胞数组
   >> Cell{1}
   
   ans =
   
       'Harry'
   
   >> Cell{2}
   
   ans =
   
       15
   
   >> Cell{3}
   
   ans =
   
        1     0
       15     2
   

   而使用圆括号形式的索引可以得到变量的描述，如下：

   >> Cell(3)
   
   ans =
   
     1×1 cell 数组
   
       {2×2 double}
   

2. 结构体

   结构体是另一种形式的聚合类型。如下：

   >> %定义结构体
   >> Struct.Name = 'Harry';
   >> Struct.Age = 15;
   >> Struct.SalaryMatrix = [1 0; 15 2];
   >> 
   >> Struct %显示结构体内容
   
   Struct = 
   
     包含以下字段的 struct:
   
               Name: 'Harry'
                Age: 15
       SalaryMatrix: [2×2 double]
   
   >> %访问结构体内部的字段
   >> name = Struct.Name;
   >> name
   
   name =
   
       'Harry
   

1.5.7、关系运算与逻辑运算

关系运算的结果是布尔量（0 或 1），如下：

运算	符号	运算	符号
大于	>	小于	<
大于等于	≥	小于等于	≤
等于	=	不等于	≠

逻辑运算，如下：

运算	符号	运算	符号
与	&	或	|
非	~	异或	Xor

1.5.8、常见图像处理数学函数

Matlab 最为强大的功能是依靠函数实现的，这些函数可能是 Matlab 内置的，也可能是由 M 文件提供的。

函数	用途
all	是否所有元素非零
any	是否至少有一个元素非零
isempty	是否空矩阵
isequal	是否两矩阵相同
isinf	判断有无 inf 元素
isnan	判断有无 nan 元素
isreal	判断是否实矩阵
find	返回一个由非零元素下标组成的矩阵
det	计算方阵对应的行列式
diag	抽取对角线元素
eig	求特征值和特征向量
fliplr	左右翻转
flipud	上下翻转
inv	求逆矩阵
lu	三角分解
norm	求范数
orth	正交化
poly	求特征多项式
qr	正交三角分解
rank	求矩阵的秩
svd	奇异值分解
trace	求矩阵的迹
Tril	抽取上三角阵
Tnu	抽取下三角阵

1.5.9、Matlab 程序流程控制

语句	规范写法	备注
if…elseif… else	if expression 1 statements 1 elseif expression 1 statements 2 else expresion 3 statements 3 end	如果 elseif 使用的层次较多时，可以考虑 switch
for	for index=start:increment:end statements end	increment 指定步进值，省略则默认为 1。可以嵌套使用
while	while expression statements end	同样可以嵌套
break	-	终止 while 或 for 循环的执行
continue	-	直接跳到下一个循环
switch	switch expression 1 case expression 1 statements 1 case expression 2 statements 2 otherwise statement_other end	没有默认的 fall_through，因而不需要使用配套的 break 语句
return	-	返回调用函数

• meshgrid 函数

  meshgrid 函数用于根据给定的横坐标点生成坐标网格，以便计算二元函数的取值，在绘制三维曲面时常常用到它。其调用方式如下：

  [X,Y] = meshgrid(x,y)
  

  参数说明

  • x 为输入的横坐标
  • y 为输入的纵坐标

  返回值

  • X 和 Y 为输入采样点的横坐标矩阵和纵坐标矩阵，X 和 Y 的元素分别为对应位置点的横坐标和纵坐标。

  下面以绘制二维高斯函数曲面为例说明 meshgrid 的用法。

  中心在原点的二维高斯函数表达式如下：
  $$H(u,v)=e^{-[u^2+v^2]/2{\sigma }^2}$$
  下面的程序分别为 u 和 v 赋值[-10:0.1:10]，令 σ = 3，使用 meshgrid 函数生成网格，并计算函数值（注意：这里使用的是 .^ 和 ./），然后使用 mesh 函数将其显示到绘图窗口中。

  >> u = [-10:0.1:10];
  >> v = [-10:0.1:10];
  >> [U,V] = meshgrid(u,v);
  >> H = exp(-(U.^2 + V.^2)./2/3^2);
  >> mesh(u,v,H);
  >> % mesh 函数是绘制三维曲面的函数，第一个和第二个参数分别是 x 轴和 y 轴的坐标点序列，第三个参数为在由坐标点序列确定的每一个方格点上的函数值
  

1.5.10、M 文件编写

M 文件和 C/C++ 中 c/cpp 文件类似，就是存储 Matlab 代码的并可执行的文件。Matlab 的源代码文件可以直接执行而不需要编译（也可以使用编译来使代码运行得更快）。很多情况下，M 文件用于封装一个功能函数从而提供某些特定功能。

1.5.11、Matlab 函数的编写

1. 函数语法

   Matlab 函数通常在 M 文件中定义，一个文件可以定义多个函数。一个 Matlab 函数通常包含以下几个部分。

   • 函数定义行

     function [outputs] = name(inputs)
     

     Matlab 允许返回多个参数（outputs），如果只返回一个参数，可以省略方括号。需要注意的是，输入参数是使用圆括号括起来的。

     某些函数可能没有输出参数，那么就需要在省略方括号及其中内容的同时，省略等号。

     函数可以在其他的 M 函数中被调用，也可以在命令行直接调用。调用函数的方法很简单，只需要写出函数定义中除了 function 之外的部分即可。

   • “H1” 行

     “H1” 行是 M 文件中的第一个注释行（即以百分号开始的行），它必须紧跟着函数定义行，中间不能有空行，这一行的百分号前也不能有空白字符或缩进，这一行的内容将在使用 help 命令时显示在第一行，而 lookfor 命令查找 H1 行中的指定关键字，并在结果的右侧显示 H1 行。

   • 函数体和备注

---

2、Matlab 图像类型及其存储方式

2.1、亮度（灰度）图像（Intensity Image）

亮度图像即灰度图像。Matlab 使用二维矩阵存储亮度图像，矩阵中的每个元素直接表示一个像素的亮度（灰度）信息。例如，一个 200 像素 × 300 像素的图像被存储为一个 200 行 300 列的矩阵。

如果矩阵元素的类型是双精度的，则元素的取值范围是 0~1；如果是 8 位无符号整数，则取值范围 0~255。数据 0 表示黑色，而 1（或 255）表示最大亮度（通常为白色）。

2.2、RGB 图像

RGB 图像使用 3 个一组的数据表达每个像素的颜色，即其中的红色、绿色和蓝色分量。在 Matlab 中，RGB 图像被存储在一个 m × n × 3 的三维数组中。对于图像中的每个像素，存储的三个颜色分量合成像素的最终颜色。

RGB 图像同样可以由双精度数组或 8 位无符号整数数组存储。

2.3、索引图像

索引图像往往包含两个数组：一个图像数据矩阵和一个颜色索引表。对应于图像中的每一个像素，图像数据数组都包含一个指向颜色索引表的索引值。

颜色索引表是一个 m × 3 的双精度型矩阵，每一行指定一种颜色的三个 RGB 分量，即 color = [R G B]。其中 R、G、B 是实数类型的双精度数，取值 0~1。0 表示全黑，1 表示最大亮度。

图像数据矩阵和颜色索引表的关系取决于图像数据矩阵中存储的数据类型是双精度类型还是 8 位无符号整数。

如果图像数据矩阵使用双精度类型存储，像素数据 1 表示颜色索引表中的第一行，像素数据 2 表示颜色索引表中的第二行，以此类推。而如果图像数据使用 8 位无符号整数存储，则存在一个额外的偏移量 -1，像素数据 0 表示颜色索引表中的第一行，而 1 表示索引表中的第二行。

2.4、二值图像（Binary Image）

在二值图像中，像素的颜色只有两个可能的情况：黑或白。Matlab 将二值图像存储为一个二维矩阵，每个元素的取值只有 0 和 1 两种情况，0 表示黑色，而 1 表示白色。

Matlab 中使用 unit8 型的逻辑数组存储二值图像，通过一个逻辑标志表示数据有效范围是 0~1，而如果逻辑标志未被置位，则有效范围为 0~255。

---

3、读取和写入图像文件

3.1、imread 函数

imread 函数可以将指定位置的图像读入工作区。对于除索引图像以外的情况，其原型如下：

A = imread(FILENAME,FMT);

参数说明

• FILENAME 指定图像文件的完整路径和文件名。如果要读入文件在当前工作目录中或者自动搜索列表中给出的路径下，则只需要提供文件名；

• FMT 参数指定图像文件的格式所对应的标准扩展名

• 返回值

  • A 是一个包含图像数据的矩阵。对于灰度图，它是一个 m 行 n 列的矩阵；对于 RGB 真彩图，则是一个 m × n × 3 的矩阵。

  • 对于索引图像，情况会有所不同，此时 IMREAD 的调用形式如下：

    [X,MAP] = imread(FILENAME,FMT);
    

    此时，X 为图像数据矩阵，MAP 则是颜色索引表。

3.2、IMWRITE 函数

imwrite 将指定的图像数据写入文件中，通过指定不同的保存文件扩展名，可以起到图像格式转换的作用。

imwrite(A,FILENAME,EMT);

参数说明

• FILENAME 参数指定文件名（不必包含扩展名）
• FMT 参数指定保存文件所采用的格式

在存储索引图像时，还需要一并存储颜色索引表，则此时 IMWRITE 函数的使用方法应为如下：

imwrite(A,MAP,FILENAME,FMT);

MAT 是合法的 Matlab 颜色索引表。

3.3、iminfo 函数

显示图像信息。

---

4、图像的显示

4.1、imshow 函数

imshow 函数用于显示工作区或图像文件中的图像，在显示的同时可控制部分效果，常用的调用形式如下：

imshow(I,[low high],param1,value1,param2,value2,...)
imshow(I,MAP)
imshow(filename)

• I 为要显示的图像矩阵；
• 可选参数 [low high] 指定显示灰度图像时的灰度范围，灰度值低于 low 的像素被显示为黑色，高于 high 的像素被显示为白色，介于 low 和 high 之间的像素被按比例显示为各种等级的灰色。如果将此参数指定为空矩阵 [ ]，则函数会将图像矩阵中的最小值指定为 low，最大值指定为 high，从而达到灰度拉伸的效果；
• 可选参数 param1,value1,param2,value2 等可以用来指定显示图像的特定方法；
• MAP 为颜色索引表，除了显示索引图像，这在显示伪彩色图像时也会用到；
• filename 为图像文件名。

4.2、多幅图像的显示

可以在同一窗口或者不同的窗口显示多幅图像。

I = imread('pout.tif');		% 读取图像

% 在不同窗口显示
figure;		% 创建一个新的窗口
imshow(I);
figure;
imshow(I,[ ]);

figure;
subplot(1,2,1);
imshow(I);
subplot(1,2,2);
imshow(I,[ ]);

4.3、像素查看工具

使用 imshow 函数显示一幅图像之后，可以通过输入 impixelinfo 命令在最后显示的图像窗口的左下角，随鼠标光标的移动显示鼠标指针所指位置处的像素值。

输入 imdistline 命令以交互的方式查看图像中两点的距离。

4.4、图像的放缩

输入 zoom on 命令可实现放缩，zoom off 关闭