sklearn机器学习:逻辑回归LogisticRegression参数解析之梯度下降

梯度下降：重要参数max_iter

在上篇博文《sklearn机器学习:逻辑回归LogisticRegression参数解析之penalty & C》中，我们解析了参数penalty & C，本文重点讨论max_iter。
逻辑回归的目的是求解能够让模型最优化、拟合程度最好的参数ω的值，即求解能够让损失函数J(ω)最小化的ω值。
对于二元逻辑回归，有多种方法可以用来求解参数ω，最常见的有梯度下降法(Gradient Descent)，坐标下降法(Coordinate Descent)，牛顿法(Newton-Raphson method)等，其中又以梯度下降法最为著名。每种方法都涉及复杂的数学原理，但这些计算在执行的任务其实是类似的。

梯度下降求解逻辑回归

以最著名也最常用的梯度下降法为例，来看逻辑回归的参数求解过程。观察下面的图像，这个图像的横坐标是参数，纵坐标是损失函数J(ω)，最简化的情况下，只有一个特征对应只有一个参数。现在求解损失函数值最小化时的ω解，执行过程如下：

1. 首先在图像上随机投掷一个小球，让小球向着损失函数最低的点去滚动
2. 由于没有重力，所以需要告诉小球三件事，才能够让小球滚动起来：
   (1) 滚动的方向：必须是损失函数的值下降最快的方向
   (2) 每次滚动的距离
   (3) 要滚动的次数
   
   然而真正的损失函数可能会长这样：
   
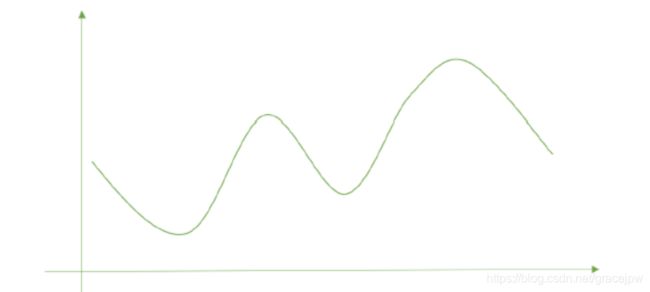
   现在有一个带两个特征并且没有截距的逻辑回归y(x₁,x₂)，两个特征所对应的参数分别为(ω₁,ω₂)。下面这个华丽的平面就是损失函数J(ω₁,ω₂)在以ω₁、ω₂和J为坐标轴的三维立体坐标系上的图像。现在，寻求的是损失函数的最小值，也就是图像的最低点。
   
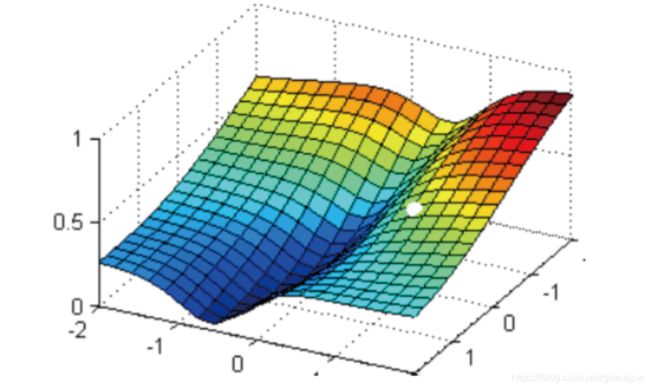
   在这个图像上随机放一个小球，松手，这个小球就会顺着这个华丽的平面滚落，直到滚到深蓝色的区域——损失函数的最低点。同样，为了严格监控这个小球的行为，让小球每次滚动的距离有限，不让他一次性滚到最低点，并且最多只允许它滚动100步，还要记下它每次滚动的方向，直到它滚到图像上的最低点。
   可以看到，小球高处滑落，在深蓝色的区域中来回震荡，最终停留在了图像凹陷处的某个点上。可以观察到几个现象：
   首先，小球并不是一开始就直向着最低点去的，它先一口气冲到了蓝色区域边缘，后来又折回来，已经规定了小球是多次滚动，所以可见，小球每次滚动的方向都是不同的。
   另外，小球在进入深蓝色区域后，并没有直接找到某个点，而是在深蓝色区域中来回震荡了了数次才停下。这有两种可能：1) 小球已经滚到了了图像的最低点，所以停下了，2) 由于设定的步数限制，小球还没有找到最低点，但也只好在100步的时候停下了。也就是说，小球不一定滚到了图像的最低处。
   但无论如何，小球停下的是我们在现有状况下可以获得的唯一点。如果够幸运，这个点就是图像的最低点，那只要找到这个点的对应坐标( ${\omega }_1^{\ast },{\omega }_2^{\ast },J_{min}$)，就可以获取能够让损失函数最小的参数取值$[{\omega }_1^{\ast },{\omega }_2^{\ast }]$。如此，梯度下降的过程就已经完成。
   在此过程中，小球其实就是一组组的坐标点（ω₁,ω₂,J）；小球每次滚动的方向就是那一个坐标点的梯度向量方向，因为每滚动一步，小球所在的位置都发生变化，坐标点和坐标点对应的梯度向量都发生变化，所以每次滚动的方向也都不一样；人为设置的100次滚动限制，就是sklearn中逻辑回归的参数max_iter，代表着能走的最大步数，即最大迭代次数。每次滚动的距离限制，由“步长“决定，在sklearn中是被提前定义好的，人为不可控。
   所以梯度下降，其实就是在众多可能的值中遍历，一次次求解坐标点的梯度向量，不断让损失函数的取值逐渐逼近最小值，再返回这个最小值对应的参数取值$[{\omega }_1^{\ast },{\omega }_2^{\ast }]$的过程。

梯度下降

在多元函数上对各个自变量量求∂偏导数，把求得的各个自变量量的偏导数以向量的形式写出来，就是梯度。比如损失函数J(ω₁,ω₂)，其自变量是逻辑回归预测函数y_ω(x)的参数ω₁,ω₂，在损失函数上对ω₁,ω₂求偏导数，求得的梯度向量d就是$[\frac{\partial J}{\partial {\omega }_1},\frac{\partial J}{\partial {\omega }_2}{]}^T$，简称grad J(ω₁,ω₂)或者$\nabla J({\omega }_1,{\omega }_2)$。在ω₁,ω₂和J的取值构成的坐标系上，点$({\omega }_1^{\ast },{\omega }_2^{\ast },J)$具体的梯度向量就是$[\frac{\partial J}{\partial {{\omega }_1}^{\ast }},\frac{\partial J}{\partial {{\omega }_2}^{\ast }}{]}^T$，或者$\nabla J({\omega }_1^{\ast },{\omega }_2^{\ast })$。如果是3个参数的梯度向量量，就是$[\frac{\partial J}{\partial {\omega }_1},\frac{\partial J}{\partial {\omega }_2},\frac{\partial J}{\partial {\omega }_3}{]}^T$，以此类推。

到底在哪个函数上，求什么的偏导数？

有些讲解梯度向量的定义的句子，比如“对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度”。这种解释一眼看上去没错，却不太严谨。
一个多元函数的梯度，是对其自变量求偏导的结果，不是对其参数求偏导的结果。但是在逻辑回归的数学过程中，损失函数的自变量量刚好是逻辑回归的预测函数y(x)的参数，所以才造成了这种让人误解的“对多元函数的参数求偏导”的写法。务必记住，正确的做法是：在多元函数(损失函数)上对自变量量(逻辑回归的预测函数y(x)的参数)求偏导，求解梯度的方式，和逻辑回归本身的预测函数y(x)没有丝毫关系。
以及，以f(x)作为例子，解释说梯度向量是(∂f/∂x,∂f/∂y)^T。这种举例方式又
会造成误解：“ x是逻辑回归中的特征呀，所以梯度向量是对模型的特征，即x求偏导数”。这个例子，其实是对多元函数的自变量求偏导数，并不是代表在逻辑回归中要对特征求偏导数。
求解梯度，是在损失函数上对损失函数J(ω₁,ω₂)自身的自变量ω₁,ω₂求偏导，而这两个自变量，刚好是逻辑回归的预测函数$y(x)=\frac{1}{1+e^{-{\omega }^{T}x}}$的参数。
梯度是什么？梯度是一个向量，因此它有大小也有方向。它的大小，就是偏导数组成的向量的大小，又叫做向量的模，记作d。它的方向，几何上说，就是损失函数J(ω)的值增加最快的方向，就是小球每次滚动的方向的反方向。只要沿着梯度向量的反方向移动坐标，损失函数J(ω)的取值就会减少得最快，也就最容易找到损失函数的最小值。
在逻辑回归中，损失函数如下所示：

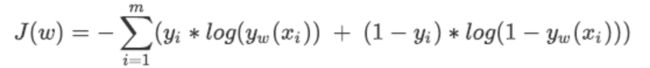
对这个函数的自变量ω求偏导，就可以得到梯度向量在第j组ω的坐标点上的表示形式：

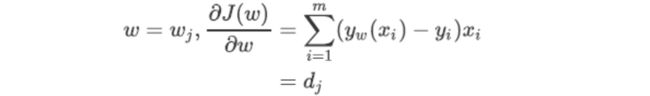
在这个公式下，只要给定一组ω的取值，再带入特征矩阵x，就可以求得这一组ω取值下的预测结果y_ω(x_i)，结合真实标签向量y，就可以获得这一组ω_j取值下的梯度向量，其大小表示为d_j。
我们的目的是在可能的ω取值上进行遍历，一次次计算梯度向量，并在梯度向量的反方向上让损失函数J下降至最小值。在这个过程中，ω和梯度向量的大小d都会不断改变，而遍历过程可以描述为：

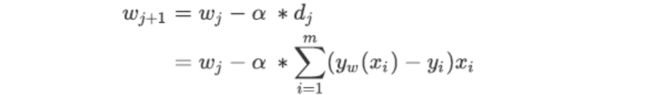
其中ω_j+i是第j次迭代后的参数向量，ω_j是第j次迭代后的参数向量，α被称为步长，控制着每走一步（每迭代一次）后ω的变化，并以此来影响每次迭代后的梯度向量的大小和方向。

步长

步长到底是什么？

有些资料中，步长被描述为”梯度下降中每一步沿梯度的反方向前进的长度“，”沿着最陡峭最易下山的位置走的那一步的长度“或者”梯度下降中每一步损失函数减小的量“，甚至有说，步长是二维平面著名的求导三角形中的”斜边“或者“对边”的。这些说法都是错误的。
来看下面这张二维平面的求导三角型图。类比到损失函数和梯度概念上，图中的抛物线就是损失函数J(ω)，A(ω_a,J(ω_a))就是小球最初在的位置，B(ω_b,J(ω_b))就是一次滚动后小球移动到的位置。从A到B的方向就是梯度向量的反方向，指向损失函数在A点下降最快的方向。而梯度向量的大小是点A在图像上对ω求导后的结果，也是点A切线方向的斜率，橙色角的tan结果，记作d。

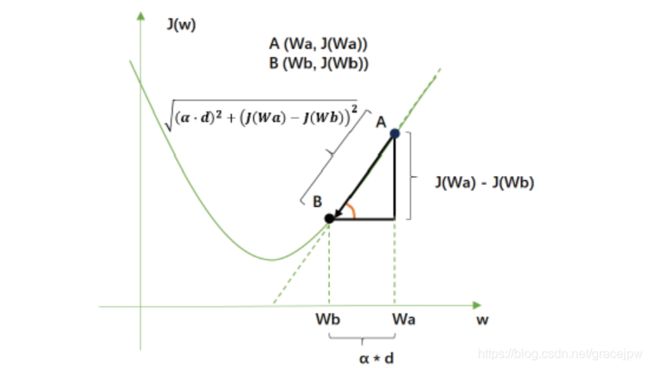
梯度下降每走一步，损失函数减小的量，是损失函数在ω变化之后的取值变化，写作J(ω_b)-J(ω_a)，这是二维平面的求导三角型中的“对边”。
梯度下降每走一步，参数向量的变化，写作ω_a-ω_b，根据我们参数向量的迭代公式，就是"步长x梯度向量"的大小，记作$\alpha \ast d$ ，这是二维平面的求倒三角形中的“邻边”。
梯度下降中每走一步，下降的距离，是$\sqrt{(\alpha \ast d{)}^2+(J({\omega }_b)-J({\omega }_a){)}^2}$，是对边和邻边的根号下平方和，是二维平面的求导三角型中的”斜边“。
所以，步长不是任何物理距离，它甚至不是梯度下降过程中任何距离的直接变化，它是梯度向量的大小d上的一个比例，影响着参数向量每次迭代后改变的部分。
不难发现，既然参数迭代是靠梯度向量的大小d * 步长α来实现的，而J(ω)的降低又是靠调节ω来实现的，所以步长可以调节损失函数下降的速率。在损失函数降低的方向上，步长越长，ω的变动就越大。
相对的，步长如果很短，ω的每次变动就很小。具体地说，如果步长太大，损失函数下降得就非常快，需要的迭代次数就很少，但梯度下降过程可能跳过损失函数的最低点，无法获取最优值。而步长太小，虽然函数会逐渐逼近我们需要的最低点，但迭代的速度却很缓慢，迭代次数就需要很多。

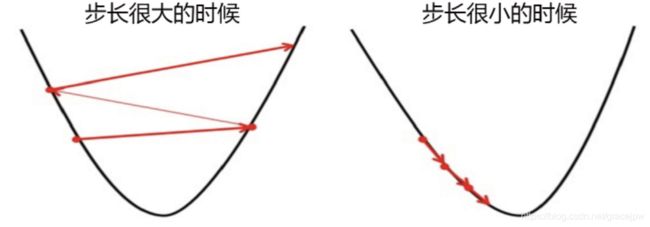
看小球运动时注意到，小球在进入深蓝色区域后，并没有直接找到某个点，而是在深蓝色区域中来回震荡了数次才停下，这种”震荡“其实就是因为我们设置的步长太大的缘故。但是在开始梯度下降之前，我们并不知道什么样的步长才合适，但梯度下降一定要在某个时候停止才可以，否则模型可能会无限地迭代下去。因此，sklearn中，设置参数max_iter最大迭代次数来代替步长，帮助我们控制模型的迭代速度并适时地让模型停下。max_iter越大，代表步长越小，模型迭代时间越长，反之，则代表步长设置很大，模型迭代时间很短。
迭代结束，获取到J(ω)的最小值后，我们就可以找出这个最小值对应的参数向量ω，逻辑回归的预测函数也就可以根据这个参数向量ω来建立了。
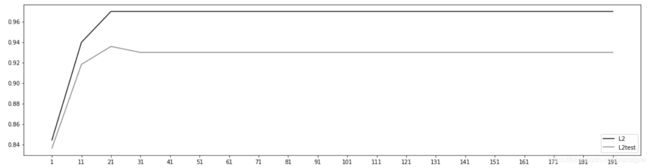
来看看乳腺癌数据集下，max_iter的学习曲线：

#乳腺癌数据集下，max_iter的学习曲线
l2 = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.arange(1,201,10):
    lrl2 = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=i)
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l2,l2test]
color = ["black","gray"]
label = ["L2","L2test"]
plt.figure(figsize=(20,5))
for i in range(len(graph)):
    plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i])
plt.legend(loc=4)
plt.xticks(np.arange(1,201,10))
plt.show()

#可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
lr = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=300).fit(Xtrain,Ytrain)
lr.n_iter_

array([25], dtype=int32)