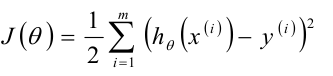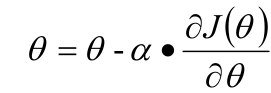1.梯度下降法
除了最小二乘法还可以使用梯度下降求解。
我们先随机给θ一个值,然后朝着负梯度的方向移动,也就是迭代,每次得到的θ值使用J(θ)比之前更小。
我们函数y = (x - 0.1)²/2为例,使用梯度下降的方法,求其y达到最小时,x的值
代码示例
# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import font_manager
font = font_manager.FontProperties(fname="/usr/share/fonts/wps-office/msyhbd.ttf", size=25)
class OneGard(object):
def __init__(self,fx,hx):
"""
:param fx: 原函数
:param hx: 导函数
"""
self.fx = fx
self.hx = hx
self.x = None
self.GD_X = []
self.GD_Y = []
self.iter_num = 0
self.f_change = None
self.f_current = None
def gard_fun(self,x, alpha=0.5):
"""
梯度下降
:param x: 初始随机x值
:param alpha: 学习率
:return:
"""
self.x = x
self.f_change = self.fx(self.x)
self.f_current = self.f_change
self.GD_X.append(x)
self.GD_Y.append(self.f_current)
while self.f_change > 1e-10 and self.iter_num < 100:
self.iter_num += 1
self.x = self.x - alpha * self.hx(self.x)
tmp = self.fx(self.x)
self.f_change = np.abs(self.f_current - tmp)
self.f_current = tmp
self.GD_X.append(self.x)
self.GD_Y.append(self.f_current)
def f(x):
"""
y = (x - 0.1)²/2
:param x:
:return:
"""
return (x - 0.1) ** 2 /2
def h(x):
"""
y = (x - 0.1)²/2的导数
:param x:
:return:
"""
return (x - 0.1)
gard = OneGard(f, h)
gard.gard_fun(x=4,alpha=0.5)
print("最终x:{:.2f},y:{:.2f}" .format(gard.x, gard.f_current))
print("迭代次数{}" .format( gard.iter_num))
print("迭代过程x的取值:\n{}".format(gard.GD_X))
# 画图
X = np.arange(-4, 4.5, 0.05)
Y = np.array(list(map(lambda t: f(t), X)))
plt.figure(figsize=(20,10), facecolor='w')
plt.plot(X, Y, 'r-', linewidth=2)
plt.plot(gard.GD_X, gard.GD_Y, 'bo--', linewidth=2)
plt.show()
结果为
最终x:0.10,y:0.00
迭代次数19
迭代过程x的取值:
[4, 2.05, 1.075, 0.5874999999999999, 0.34374999999999994, 0.221875, 0.1609375, 0.13046875000000002, 0.11523437500000001, 0.10761718750000002, 0.10380859375000001, 0.10190429687500001, 0.1009521484375, 0.10047607421875, 0.10023803710937501, 0.10011901855468751, 0.10005950927734375, 0.10002975463867188, 0.10001487731933595, 0.10000743865966798]图像如下: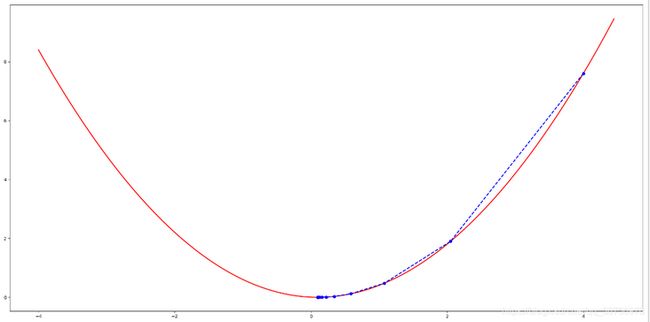
机器学习中梯度下降常用的有三种:
批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD)。
参考 梯度下降法的三种形式BGD、SGD以及MBGD
(这个写的清楚明了,以前学的时候,脑子听成了浆糊,看了这篇文,我是豁然开朗)
2.多项式回归
线性回归针对的是θ而言是一种,对于样本本身而言,样本可以是非线性的。
例如![]()
这时我们可以领x1 = x, x2 = x²,
得到如下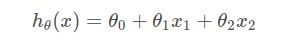
这样就转变成我们的熟悉的线性回归。
多项式扩展,就是将低纬度空间的点映射到高纬度空间中。
3.其他线性回归
3.1Ridge回归
线性回归的L2正则化通常称为Ridge回归,也叫作岭回归,与标准线性回归的差异,在于它在损失函数上增加了一个L2正则化的项。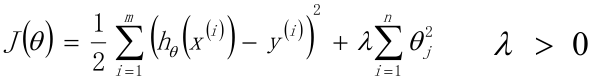
λ是常数系数,是正则化系数,属于一个超参数,需要调参。
λ太小就会失去处理过拟合的能力,太大就会因力度过大而出现欠拟合的现象。
3.2 LASSO回归
使用L1正则的线性回归模型就称为LASSO回归,和Ridge回归区别在于,它加的是L1正则化的项。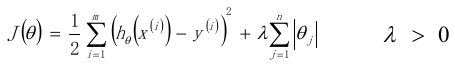
3.3 弹性网络
弹性网络,Elasitc Net,同时使用L1正则和L2正则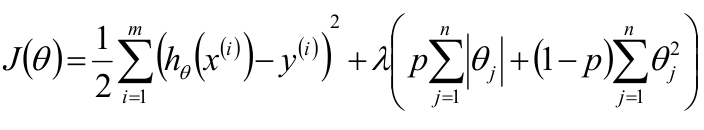
3.4 Ridge回归和LASSO回归比较
1)两者都可以都可以来解决标准线性回归的过拟合问题。
2)LASSO可以用来做特征选择,但Ridge回归则不行,因为LASSO能够使得不重要的变量的系数变为0,而Ridge回归则不行。
参考 线性回归、lasso回归、岭回归以及弹性网络的系统解释
4.代码示例
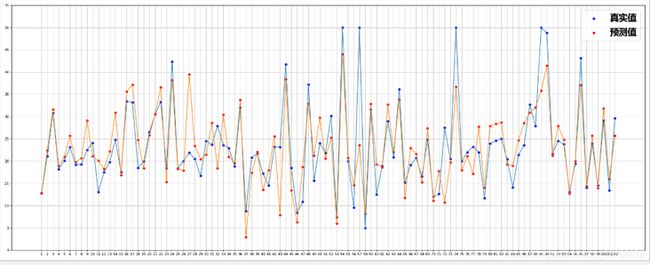
岭回归预测波士顿房价
from sklearn.datasets import load_boston
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from matplotlib import pyplot as plt
from matplotlib import font_manager
font = font_manager.FontProperties(fname="/usr/share/fonts/wps-office/msyhbd.ttf", size=25)
def radge_fun():
"""
岭回归预测波士顿房价
:return:
"""
lb = load_boston()
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.2)
x_std = StandardScaler()
y_std = StandardScaler()
x_train = x_std.fit_transform(x_train)
x_test = x_std.transform(x_test)
y_train = y_std.fit_transform(y_train.reshape(-1,1))
y_test = y_std.transform(y_test.reshape(-1,1))
model = Ridge(alpha=1.0)
model.fit(x_train, y_train)
y_predict = y_std.inverse_transform(model.predict(x_test))
return y_predict, y_std.inverse_transform(y_test)
def draw_fun(y_predict, y_test):
"""
绘制房价预测与真实值的散点和折线图
:param y_predict:
:param y_test:
:return:
"""
x = range(1,len(y_predict)+1)
plt.figure(figsize=(25, 10), dpi=80)
plt.scatter(x, y_test, label="真实值",color='blue')
plt.scatter(x, y_predict,label='预测值', color='red')
plt.plot(x,y_test)
plt.plot(x,y_predict)
x_tick = list(x)
y_tick = list(range(0,60,5))
plt.legend(prop=font, loc='best')
plt.xticks(list(x), x_tick)
plt.yticks(y_tick)
plt.grid(alpha=0.8)
plt.show()
if __name__ == '__main__':
y_predict, y_test = radge_fun()
draw_fun(y_predict, y_test)