数组在上一篇的专栏,中我们进行了回顾和刷题。
链表
趁热打铁,我们来对比数组来学习链表。
首先要明确的是,链表和数组的底层存储结构不同,数组要求存储在一块连续的内存中,而链表是通过指针将一组零散的内存块串联起来。
可见链表对内存的要求降低了,但是随机访问的性能就没有数组好了,需要 O(n) 的时间复杂度。
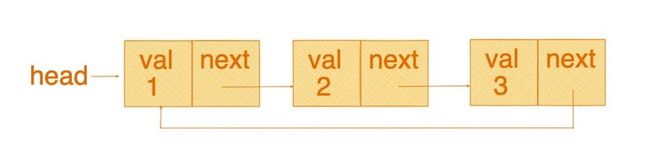
下图中展示了单链表及单链表的添加和删除操作,其实链表操作的本质就是处理链表结点之间的指针。
在删除链表结点的操作中,我们只需要将需要删除结点的前驱结点的 next 指针,指向其后继即可。这样,当前被删除的结点就被丢弃在内存中,等待着它的是被垃圾回收器清除。
为了更便于你理解,链表可以类比现实生活中的火车,火车的每节车厢就是链表的一个个结点。车厢之间相互连接,可以添加或者移除掉。春运时,客运量比较大,列车一般会加挂车厢。
链表的结点结构由数据域和指针域组成,在 JavaScript 中,以嵌套的对象形式实现。
{
// 数据域
val: 1,
// 指针域
next: {
val:2,
next: ...
}
} 名词科普
- 头结点:头结点用来记录链表的基地址,是我们遍历链表的起点
- 尾结点:尾结点的指针不是指向下一个结点,而是指向一个空地址 NULL
- 单链表:单链表是单向的,它的结点只有一个后继指针 next 指向后面的结点,尾结点指针指向空地址
- 循环链表:循环链表的尾结点指针指向链表的头结点
- 双向链表:双向链表支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个前驱指针 prev 指向前面的结点,双向链表会占用更多的内存,但是查找前驱节点的时间复杂度是 O(1) ,比单链表的插入和删除操作都更高效
- 双向循环链表
循环链表
双向链表
双向循环链表
开启刷题
年初立了一个 flag,上面这个仓库在 2021 年写满 100 道前端面试高频题解,目前进度已经完成了 50%。
如果你也准备刷或者正在刷 LeetCode,不妨加入前端食堂,一起并肩作战,刷个痛快。
了解了链表的基础知识后,马上开启我们愉快的刷题之旅,我整理了 6 道高频的 LeetCode 链表题及题解如下。
01 删除链表的倒数第 N 个结点
快慢指针
先明确,删除倒数第 n 个结点,我们需要找到倒数第 n+1 个结点,删除其后继结点即可。
- 添加 prev 哨兵结点,处理边界问题。
- 借助快慢指针,快指针先走 n+1 步,然后快慢指针同步往前走,直到 fast.next 为 null。
- 删除倒数第 n 个结点,返回 prev.next。
const removeNthFromEnd = function(head, n) {
let prev = new ListNode(0), fast = prev, slow = prev;
prev.next = head;
while (n--) {
fast = fast.next;
}
while (fast && fast.next) {
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;
return prev.next;
}- 时间复杂度:O(n)
- 空间复杂度:O(1)
02 合并两个有序链表
思路
- 使用递归来解题
- 将两个链表头部较小的一个与剩下的元素合并
- 当两条链表中的一条为空时终止递归
关键点
- 掌握链表数据结构
- 考虑边界情况
复杂度分析
n + m 是两条链表的长度
- 时间复杂度:O(m + n)
- 空间复杂度:O(m + n)
const mergeTwoLists = function (l1, l2) {
if (l1 === null) {
return l2;
}
if (l2 === null) {
return l1;
}
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}03 两两交换链表中的节点
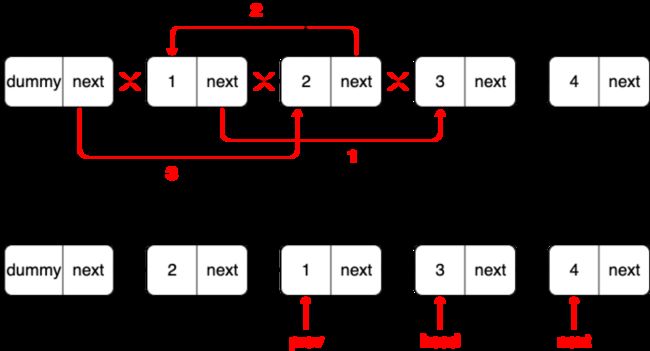
先明确想要交换节点共需要有三个指针进行改变。
- 所以我们需要在链表头部添加一个哨兵节点
- 循环中首先操作三个指针完成节点交换
- 指针右移,进行下一对节点的交换
迭代 + 哨兵节点
const swapPairs = (head) => {
const dummy = new ListNode(0);
dummy.next = head; // 头部添加哨兵节点
let prev = dummy;
while (head && head.next) {
const next = head.next; // 保存 head.next
head.next = next.next;
next.next = head;
prev.next = next;
// 下面两个操作将指针更新
prev = head;
head = head.next;
}
return dummy.next;
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
递归
如果你对递归还觉得掌握的不够透彻,可以移步我的这篇专栏
回到本题的递归解法:
- 写递归解法的话,老套路,先明确终止条件,链表中没有节点或只有一个节点时无法进行交换。
- 接下来递归的进行两两交换节点并更新指针关系。
- 返回新链表的头节点 newHead。
const swapPairs = function (head) {
// 递归终止条件
if (head === null || head.next === null) {
return head;
}
// 获得第 2 个节点
let newHead = head.next;
// 将第 1 个节点指向第 3 个节点,并从第 3 个节点开始递归
head.next = swapPairs(newHead.next);
// 将第 2 个节点指向第 1 个节点
newHead.next = head;
return newHead;
}- 时间复杂度:O(n)
- 空间复杂度:O(n)
04 环形链表
快慢指针
- 使用快慢不同的两个指针遍历,快指针一次走两步,慢指针一次走一步。
- 如果没有环,快指针会先到达尾部,返回 false。
- 如果有环,则一定会相遇。
const hasCycle = function(head) {
if (!head || !head.next) return false;
let fast = head.next;
let slow = head;
while (fast !== slow) {
if (!fast || !fast.next) {
return false;
}
fast = fast.next.next;
slow = slow.next;
}
return true;
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
标记法
遍历链表,通过 flag 标记判断是否有环,如果标记存在则有环。(走过的地方插个旗子做标记)
const hasCycle = function(head) {
while (head) {
if (head.flag) {
return true;
} else {
head.flag = true;
head = head.next;
}
}
return false;
}- 时间复杂度:O(n)
- 空间复杂度:O(1)
05 反转链表
迭代
- 初始化哨兵节点 prev 为 null,及当前节点 curr 指向头节点。
- 开始迭代,记录 next 指针留备后用,反转指针。
- 推进指针继续迭代,最后返回新的链表头节点 prev。
const reverseList = function(head) {
let prev = null;
let curr = head;
while (curr !== null) {
// 记录 next 节点
let next = curr.next;
// 反转指针
curr.next = prev;
// 推进指针
prev = curr;
curr = next;
}
// 返回翻转后的头节点
return prev;
};- 时间复杂度: O(n)
- 空间复杂度: O(1)
递归
const reverseList = function(head) {
if (!head || !head.next) return head;
// 记录当前节点的下一个节点
let next = head.next;
let reverseHead = reverseList(next);
// 操作指针进行反转
head.next = null;
next.next = head;
return reverseHead;
};- 时间复杂度: O(n)
- 空间复杂度: O(n)
06 链表的中间结点
快慢指针
老套路,借助快慢指针,fast 一次走两步,slow 一次走一步,当 fast 到达链表末尾时,slow 就处于链表的中间点了。
const middleNode = function(head) {
let fast = head, slow = head;
while (fast && fast.next) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
};- 时间复杂度: O(n)
- 空间复杂度: O(1)
![]()