本文来源于基迪奥推文。
1、structure图的由来
“Structure图”名词本身来自这种图形的分析软件——STRUCTURE。这个软件是由斯坦福大学Pritchard实验室开发的一款群体结构分析软件,最早在2000年发表在《Genetics》上[1]。
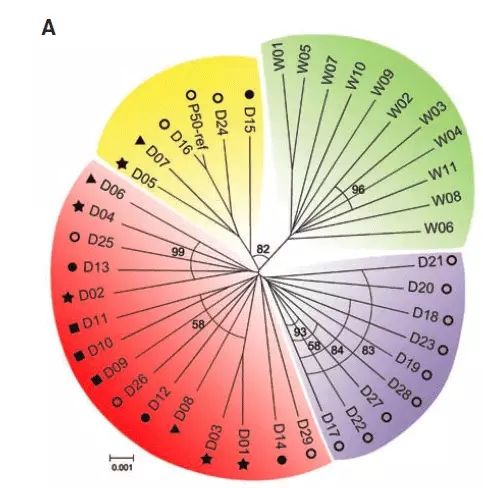
Structure软件分析达到的目的其实也很简单——分析群体的结构。要获知群体的结构,其实在前两篇与大家分享的两个图形也是可以解决的——PCA和树。通过树形图或PCA散点图,我们也可以直观了解个体间的分类关系(如图3)。但如果需要解答:这个群体应该分为3个亚群还是4个亚群更合理,群体间是否存在基因交流(直白的说法:是否有杂交),以及每个个体混血程度是多少?对于PCA图和树形图,这解决不了,那么这时候我们就用到了structure图。
2、structure图形的解读
Structure图在开发之初,就使用了与进化树或PCA截然不同的算法,所以能够解决后两者不能解决的问题。具体的算法思路我在下文会解释,我们先直接解读structure图形的意义。当然,我们也不能完全不懂structure的基本原理就直接解读structure图。
Structure分析的基本思路过程是:
1、获得一系列样本的基因型;
2、在大部分情况下,我并不知道这个群体实际包含几个亚群。我们把群体的亚群数称为K值。那么我可以预设群体亚群数等于1n,即K=1n。那么软件就会模拟在K=x的情况下,使用贝叶斯算法推算群体是如何分群的,以及每个个体的血统构成是如何的。
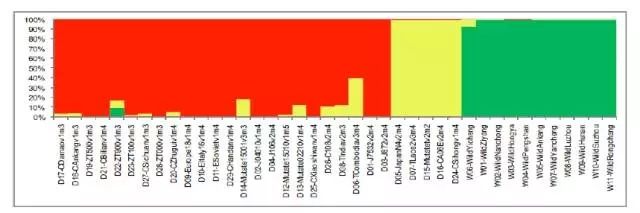
例如图4,就是在蚕重测序文章中[2]假设群体结构数的先验值K=2~4的模拟结果。以K=3的模拟结果为例。这个图形本质上就是1个堆叠图,每个直方柱子就是代表1个样本(这里是40个品种的蚕),柱子的颜色以及颜色比例代表这个样本属于哪个亚群以及血统构成比例是多少。我们很直观的通过颜色就可以判断这40个个体是如何划分为3个亚群体(红、黄、绿)。
而且,我们可以看到某些样本的血统是很纯正的(1种颜色),而某些样本却由2~3个颜色组成。例如放大图中的样本D06为例,它对应的直方柱子由两种颜色构成,大概是40%的黄色和60%的红色。说明这个个体很有可能是从两个祖先亚群杂交而来,且两个祖先亚群各占了40%和60%的血统。
以此类推,我们就可以解读在k=2、3、4的情况下,这些样本是如何分群的,以及每个样本的血统构成是多少。
先验假设K=2~4,而且每个K值假设都对应1个图形。到底哪个假设是最正确呢?
因为structure是基于贝叶斯模型的计算方法,对每个K值模拟的结果,都会对应产生最大似然值(likelihood)。这个软件的最大似然值是取了自然对数后输出的(ln likelihood)。ln likelihood越大,说明K值越接近于真实情况(记住ln likelihood是小于0的,所以我说的这个值越大越好,就是绝对值越小越好)。当然,一般随着K值升高,ln likelihood值也会不断升高,但会慢慢进入平台期。选择最优K值的目标是要找到那个拐点。
简单说来,就是要找的一个likelihood最大(越大越可靠)而且K值最小(亚群数最少)的模拟结果,往往这样的模拟对应的K值是最接近于群体的真实情况的。具体的计算过程可以参考2006年的一篇参考文献[3],那篇文章解释非常清楚。
3、structure的计算原理
Structure是与PCA、进化树相似的方法,就是利用分子标记的基因型信息对一组样本进行分类,分子标记可以是SNP、indel、SSR… …当然,对于重测序应用的最多的还是SNP。当然,structure本质上使用了与PCA、进化树完全不同的思路。进化树和PCA本质上都是计算样本序列间的差异程度,然后利用两两差异度聚类(进化树)或降维(PCA)来实现对样本的分类。
但PCA和树的不足,如上文提到的,无法推算:
1、群体应该划分为几个亚群;
2、群体间基因交流的程度;
3、某个个体的混血程度。
但structure软件摒弃的以上的方法,先预设群体由若干亚群(k=x)构成,通过模拟算法找出在k=x的情况下,最合理的样本分类方法。最后再根据每次模拟的最大似然值,找出最适用这群体的K值。
这个过程的逻辑如下:
1.亚群内符合哈温平衡
那么,软件在如何确定样本的最优分类方法呢?其实基于一个假设:在各个亚群内部个体应该符合哈代-温伯格平衡(哈温平衡的概念可以在百度查询),那么这个亚群内的基因频率分布应该可通过哈温平衡检验。例如,现在有40个个体的1个SNP位点的基因型,我预设亚群数k=2。我先随机将40个个体分成两份,然后检验是否符合哈温平衡。如果不符合,我继续调整分类策略,直到找到一种最优的分类方法:40个个体被分为了两份,每个亚群都由若干个体构成,每个亚群内部都最大程度地符合哈温平衡。
2.每个位点是独立的
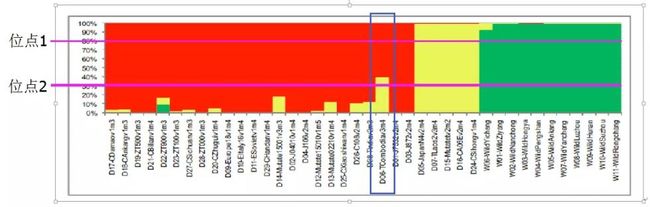
同一个体基因组上的不同SNP可能来源不同亚群体,这是由于杂交混血过程带来的效应。如下图的D06个体,就各有部分DNA来自红色和黄色的亚群体。从另一个维度理解,为了达到哈温平衡,对不同的位点的分类方法是不同的。例如下图中,位点1的分类和位点2的分类策略就不同。位点1将D06个体划为红色亚群,而位点2将D06个体划分为黄色亚群。也就是说,软件是对每个位点单独进行分群的。
3.每个样本的血统构成
既然对每个位点都完成分群了,自然最终就可以计算每个个体的血统构成了。
如果大家明白了这三个步骤了,我再以k=2为例,解释一下structure是如何找到样本的最优分类。其实简单说来,就是利用了计算机超强的运行能力,一开始计算机只是随机将样本分为两份,然后在每个亚群内进行哈温平衡检验。如果不符合哈温平衡(拍脑袋的分类,一开始当然是惨不忍睹),计算机继续调整分类,然后继续检验。
如此这般,在计算n次后,计算机再从这一堆结果中找到最佳的分类。这个过程称为“隐马科夫-蒙特卡罗链”的过程,计算次数n就是这个链的长度,这是structure一个重要的参数“Number of MCMC Reps”,需要预先设定。
但因为这个计算的过程是从随机模拟开始的。如果一开始拍脑袋拍的不好(随机分类与真实分类差距太大),计算机一黑到底,最后把n次用完了,都没有找到一个合理的分类。所以,分析软件往往有个预实验的过程。
就是在正式进行大规模运算前,计算机先尝试各种各样的随机分类,运行非常短的次数,然后评估哪种随机分类是最合理的。之后,在根据最优的随机分类,进行后续的大规模运算。这个过程就称为burn-in period,预实验的次数就称为burin-in的次数。这也是structure分析另外一个重要的参数“length of burn-in period”。
如果你理解了这两个参数ok,非常好。Structure软件最重要的两个参数你已经掌握了。剩下就选择使用那种模型了。主要涉及两种模型 no admixture model和admixture model。前者假设亚群间不存在杂交,后者则假设亚群间存在杂交。在绝大部分情况下,当然是选择admixture 模型更合理了。
4、structure分析的输入以及软件
Structure分析,输入的数据就是样本的基因型数据,注意:输入的必须是不存在连锁不平衡的独立位点。所以,对重测序的结果来说,输入所有的SNP是不对的。一来,输入的SNP数量太大,会大大拖长软件运行的时间;其次,如果使用大量存在连锁不平衡的位点,就违背了这个软件最初的假设——各个位点是独立的。正确的做法是,根据连锁不平衡衰减分析的结果,仅从所有SNP中挑选一部分独立的位点用于structure分析。
Structure分析当然最经典的软件就是STRUCTURE。但Structure分析还有其他软件可以选择[4]。比较经典的软件包括:ADMIXTURE、FRAPPE。这两个软件的运行速度都大大超过STRUCTURE。但FRAPPE的不足没有提供方法估算最佳K值。ADMIXTURE使用与STRUCTURE相同的模型,而且运行效率也很好,所以是一个比较推荐的软件。
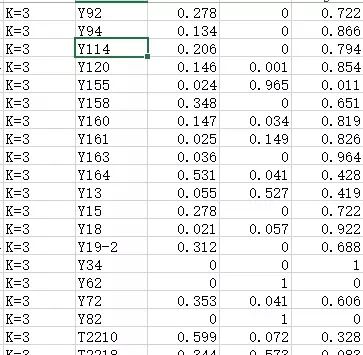
这些软件的分析结果都只是一份表格,就是每个样本的血统构成比例。要把表格变成图形的话,还有绘图的步骤。最简单的画法,你可以使用excel将这个结果绘制为堆叠图,或者也可以使用其他专门的图形化软件,例如Distruct就是比较推荐的一款将structure分析结果图形化的软件。
Structure软件是有windows的Java图形界面版本的。参数就刚刚给大家介绍的lengthof burn-in period、Number of MCMC Reps after burn-in、Admixture model。这个三个参数的设置,可以参考文献3给出的建议。两个参数各取10,000。不过随着样本数量的增加,需要适当提高参数,会让结果更可靠。