真实的三维空间中,描述物体运动状态的物理概念是运动场。三维空间中的每一个点,经过某段时间的运动之后会到达一个新的位置,而这个位移过程可以用运动场来描述。
而在计算机视觉的空间中,计算机所接收到的信号往往是二维图片信息。由于缺少了一个维度的信息,所以其不再适用以运动场描述。光流场(optical flow)就是用于描述三维空间中的运动物体表现到二维图像中,所反映出的像素点的运动向量场。
当描述部分像素时,称为:稀疏光流
当描述全部像素时,称为:稠密光流
光流法是利用图像序列中的像素在时间域上的变化、相邻帧之间的相关性来找到的上一帧跟当前帧间存在的对应关系,计算出相邻帧之间物体的运动信息的一种方法。光流法理解的关键点有:
核心问题:同一个空间中的点,在下一帧即将出现的位置
重要假设:光流的变化(向量场)几乎是光滑
角点处的光流能够通过角点的邻域完全确定下来,因此角点处的运动信息最为可靠;其次是边界的信息
光流法有着各种各样的分支,本文介绍的则是一种被广泛使用的经典稠密光流算法:Farneback 光流算法
Farneback 光流算法
作者:Gunnar Farneback
参考资料
Two-Frame Motion Estimation Based on Polynomial Expansion,提纲阅读
Polynomial Expansion for Orientation and Motion Estimation,作者博士毕业论文,深读(以下简称“博士论文”)
源码:https://searchcode.com/file/30099587/opencv_source/src/cv/cvoptflowgf.cpp
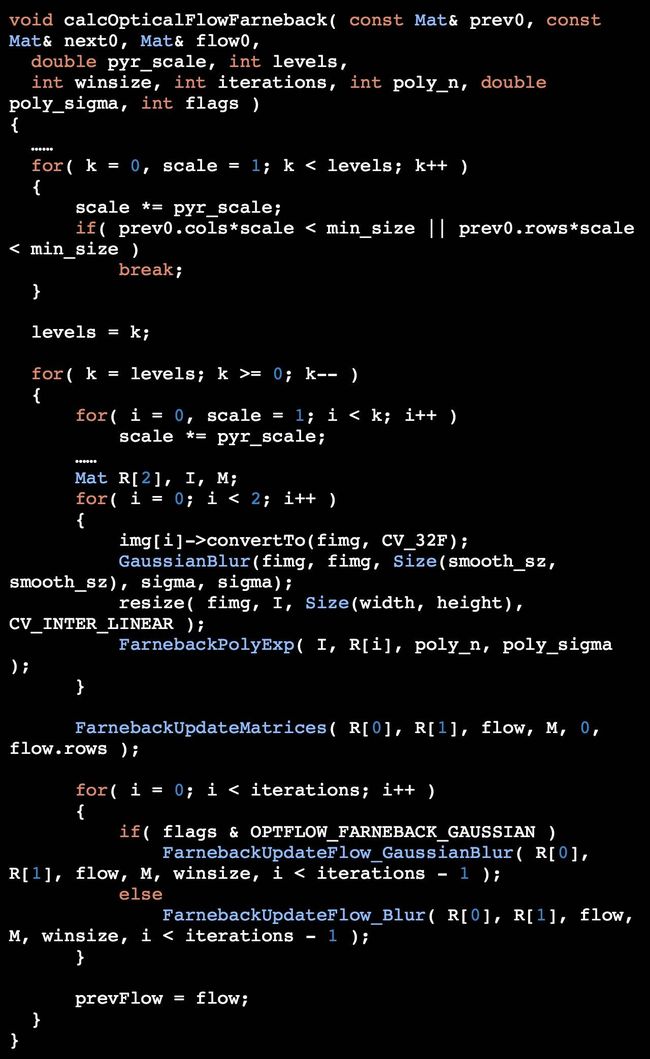
OpenCV 主函数源码解读:
源代码中为了解决孔径问题,主函数中引入了图像金字塔。
孔径问题(Aperture Problem):
http://blog.csdn.net/hankai1024/article/details/23433157
形象理解:从小孔中观察一块移动的黑色幕布观察不到任何变化。但实际情况是幕布一直在移动中
解决方案:从不同尺度(图像金字塔)上对图像进行观察,由高到低逐层利用上一层已求得信息来计算下一层信息
主函数 calcOpticalFlowFarneback 中需要的变量参数包括:
_prev0:输入前一帧图像
_next0:输入后一帧图像
_flow0:输出的光流
pyr_scale:金字塔上下两层之间的尺度关系
levels:金字塔层数
winsize:均值窗口大小,越大越能 denoise 并且能够检测快速移动目标,但会引起模糊运动区域
iterations:迭代次数
poly_n:像素邻域范围大小,一般为 5、7 等
poly_sigma:高斯标准差,一般为 1~1.5(函数处理中需要高斯分布权重)
flags:计算方法,包括 OPTFLOW_USE_INITIAL_FLOW 和 OPTFLOW_FARNEBACK_GAUSSIAN
实际的 Farneback 算法在每一层金字塔上的处理过程为:
输入的图像默认为灰度图片,默认只有亮度值
图像输入与输出时进行的高斯模糊操作(Gaussian Blur)操作都是使得光流场结果平滑,从而满足假设:光流的变化几乎是光滑的
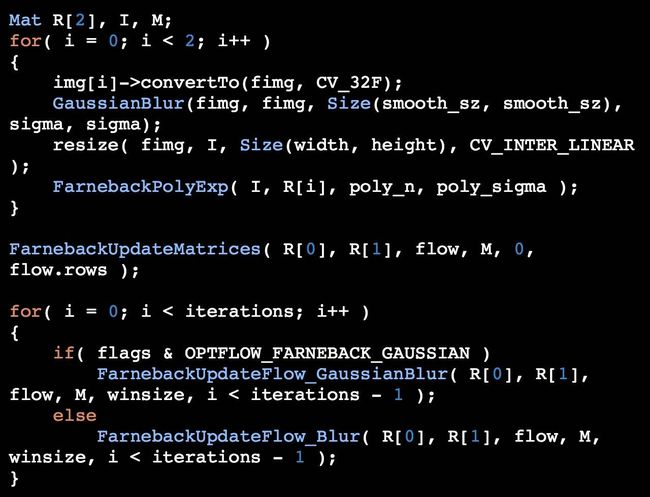
所以需要关注的子函数有 4 个:
FarnebackPolyExp
FarnebackUpdateMatrices
FarnebackUpdateFlow_GaussianBlur
FarnebackUpdateFlow_Blur
OpenCV 子函数 FarnebackPolyExp:
理论基础
图像建模
将图像视为二维信号的函数(输出图像是灰度图像),因变量是二维坐标位置 $\mathbf{x}=\left( \begin{matrix} x & y \end{matrix} \right)^T$,并且利用二次多项式对于图像进行近似建模的话,会得到:
f(\mathbf{x})\sim \mathbf{x^TAx+b^Tx+}c
其中,$\mathbf{A}$是一个2$\times$2的矩阵,$\mathbf{b}$是一个2$\times$1的矩阵
因此系数化之后,以上公式等号右侧可以写为:
\left(
\begin{matrix}
x & y
\end{matrix}
\right)^T
\left(
\begin{matrix}
r_{4} & r_{6}/2 \\
r_{6}/2 & r_{5}
\end{matrix}
\right)
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right)+
\left(
\begin{matrix}
r_{2} \\
r_{3}
\end{matrix}
\right)^T
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right)+r_{1}=r_1+r_2x+r_3y+r_4x^2+r5y^2+r_6xy
求解空间转换
如果将原有(笛卡尔坐标系)图像的二维信号空间,转换到以 $(1,x,y,x^2,y^2,xy)$ 作为基函数的空间,则表示图像需要一个六维向量作为系数,代入不同像素点的位置 $x,y$ 求出不同像素点的灰度值。
Farneback 算法对于每帧图像中的每个像素点周围设定一个邻域$(2n+1) \times (2n+1)$,利用邻域内的共$(2n+1)^2$个像素点作为最小二乘法的样本点,拟合得到中心像素点的六维系数。因此对于图像中的每个像素点,都能得到一个六维向量。
在一个邻域内灰度值的 $(2n+1) \times (2n+1)$ 矩阵中,将矩阵按列优先次序拆分组合成 $(2n+1)^2 \times 1$ 的向量 $\mathbf{f}$,同时已知 $(1,x,y,x^2,y^2,xy)$ 作为基函数的转换矩阵 $\mathbf B$ 维度为 $(2n+1)^2 \times 6$(也可以视为 6 个列向量 $\mathbf{b}_i$ 共同组成的矩阵),邻域内共有的系数向量 $\mathbf{r}$ 维度为 $6\times1$,则有:
\mathbf{f}=\mathbf B \times \mathbf r=\left(
\begin{matrix}
\mathbf b_1 & \mathbf b_2 & \mathbf b_3 & \mathbf b_4 & \mathbf b_5 & \mathbf b_6
\end{matrix}
\right) \times
\mathbf r
此处博士论文中有举例说明,非常便于理解,详见博士论文 3.4 小节
权重分配
利用最小二乘法求解时,并非是邻域内每个像素点样本误差都对中心点有着同样的影响力,函数中利用二维高斯分布将影响力赋予权重。 在一个邻域内二维高斯分布的
$(2n+1) \times (2n+1)$矩阵中,将矩阵按列优先次序拆分组合成$(2n+1)^2 \times 1$的向量$\mathbf{a}$。因此原本的基函数的转换矩阵$\mathbf B$将变为:
\mathbf B
=\left(
\begin{matrix}
\mathbf a \cdot \mathbf b_1 & \mathbf a \cdot \mathbf b_2 & \mathbf a \cdot \mathbf b_3 & \mathbf a \cdot \mathbf b_4 & \mathbf a \cdot \mathbf b_5 & \mathbf a \cdot \mathbf b_6
\end{matrix}
\right)
对偶转换(并不清楚转换的具体过程,只能参考论文中已有的公式)
为了“进一步加快求解”得到系数矩阵 $\mathbf{r}$,博士论文 4.3 小节中提出使用对偶的方式再次转换基函数矩阵 $\mathbf{B}$,此时的对偶转换矩阵为 $\mathbf{G}$,经过转换后的基函数矩阵的列向量为 $\tilde{\mathbf b_i}$。博士论文中 $\mathbf{G}$ 的计算方式为:
\mathbf G
=\left(
\begin{matrix}
(\mathbf{a \cdot b_1,b_1}) & \cdots & (\mathbf{a \cdot b_1,b_6})\\
\vdots & \ddots & \vdots \\
(\mathbf{a \cdot b_6,b_1}) & \cdots & (\mathbf{a \cdot b_6,b_6})
\end{matrix}
\right)
而通过对偶转换之后,计算系数向量 $\mathbf{r}$ 的方式就简单了很多,其中 ${\star}$ 表示两个信号的互相关(实质上类似于两个函数的卷积https://zh.wikipedia.org/wiki/%E4%BA%92%E7%9B%B8%E5%85%B3 )过程:
\mathbf{r(x)}
=
\mathbf{G}^{-1}\left(
\begin{matrix}
((\mathbf{a \cdot b_1})\star \mathbf f)(\mathbf x)\\
\vdots\\
((\mathbf{a \cdot b_6})\star \mathbf f)(\mathbf x)
\end{matrix}
\right)
函数输出
子函数 FarnebackPolyExp 输出得到的是单张图像中每个像素点的系数向量 $\mathbf r$(不包括常数项系数 $r_1$,因为之后的计算光流过程中没有用到)
Separable Normalized Convolution
博士论文 4.4 小节中提出的 Separable Normalized Convolution 计算方法提出将卷积操作由一维的直接计算拆分成两个维度的分别计算,可以降低计算复杂度,拆分的依据源自:
graph TD
A(f)
A-->B[1]
A-->C[x]
A-->D[x^2]
B-->e[1]
B-->g[y]
B-->f[y^2]
C-->h[1]
C-->i[y]
D-->j[1]
源码解读
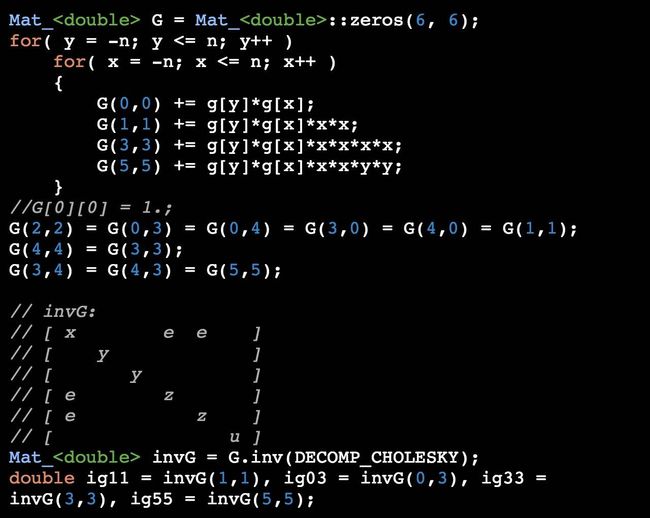
- 【基于邻域】产生二维高斯分布的基础是一维高斯分布,一维高斯分布存储于数组 g 中,并且进行了求和后归一化:
2. 【基于邻域】基于 Separable Normalized Convolution 方法,分别求解$(1,x,x^2)$上的权重分布为:
3. 【基于邻域】求解对偶转换矩阵 $\mathbf G$,注意此时的二维高斯分布权重已经被按照列向量拉伸成为了一个$(2n+1)^2 \times 1$的向量。而根据一维高斯分布数组 g 生成二维高斯分布权重也很简单,嵌套两层循环即可。循环时可以利用矩阵的对称性减少计算量。并且因为邻域中心点为 $(0,0)$点,所以循环求和时G(0,1)+=g[y]*g[x]*x这类计算在x和-x上相互抵消,结果必然为 0 无需计算:
注意:实际计算中 $G$ 的特殊结构会使得 $G^{-1}$ 的特殊结构,所以只需要保存逆矩阵中几个特殊位置的元素即可。证明过程见博士论文的附录 A
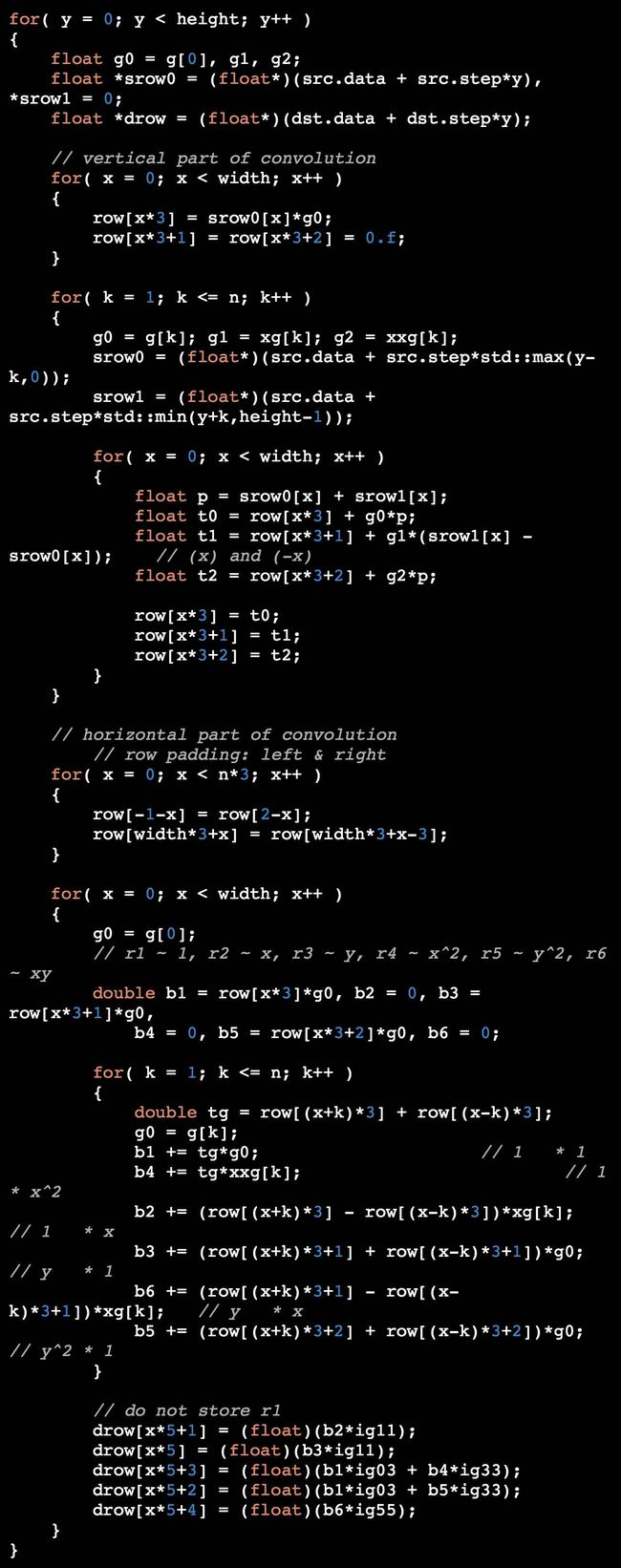
- 分别在 vertical 和 horizontal 两个方向进行卷积计算,卷积结果分别存在 row 数组和 b1~b6 中,最终的系数向量存在于 drow 数组中(不需要保存常量系数 r1,因为不涉及后面子函数的计算过程)。计算时注意
x和-x在计算时导致的正负性差异:
OpenCV 子函数 FarnebackUpdateMatrices
子函数 FarnebackUpdateMatrices 中需要的变量参数包括:
_R0:输入前一帧图像(编号:0)
_R1:输入后一帧图像(编号:1)
_flow:已知的前一帧图像光流场(用于 Blur 子函数的迭代,以及主函数中图像金字塔的不同层数间迭代)
_M:储存中间变量,不断更新
_y0:图像求解光流的起始行
-
_y1:图像求解光流的终止行
理论基础
利用 FarnebackPolyExp 函数分别得到了视频前后帧中每个像素点的系数向量之后,则需要利用系数向量计算得到光流场。这个计算过程在博士论文 7.6 小节中有描述。
首先,每个像素点都有着初始位移(最开始设置为全 0 变量),将上一帧的初始位移增加到第一帧图像上的像素点位置 $\mathbf x$ 上,得到此像素点在下一帧图像上的大致位置 $\mathbf{\tilde x}$:
\mathbf{\tilde x}=\mathbf x+\mathbf{\tilde d (x)}
$\mathbf{\tilde x}$ 可能是浮点位置,则无法估计此位置的系数向量值。对待此问题的方法有两种:
将初始位移四舍五入得到整数值(博士论文中采用)
利用二次线性插值(OpenCV 中的默认做法)
由此得到用于计算的中间变量$\mathbf{A(x)}, \mathbf{\Delta b(x)}$:
\mathbf{A(x)}=\frac{\mathbf{A_1(x)}+\mathbf{A_2(\tilde x)}}{2}
\mathbf{\Delta b(x)}=-\frac{1}{2}(\mathbf{b_2(\tilde x)-\mathbf{b_1(x)}})+\mathbf{A(x)} \mathbf{\tilde d(x)}
如果涉及到尺度变换,例如图像金字塔技术(子函数 FarnebackUpdateMatrices 中再次使用 multi-scale 的思路,但需要和主函数中的图像金字塔区分开来)。还需要另外与尺度缩放矩阵 $\mathbf{S(x)}$ 有关。总之,子函数 FarnebackUpdateMatrices 的目的是为了得到中间变量 $\mathbf{G}$ 与 $\mathbf{h}$:
\mathbf{G(x)}=\mathbf{S(x)}^T\mathbf{A(x)}^T\mathbf{A(x)S(x)}
\mathbf{h(x)}=\mathbf{S(x)}^T\mathbf{A(x)}^T\mathbf{\Delta b(x)}
源码解读
- 二次插值得到新一帧图像位置中的系数向量:
2. 处理不同尺度上的缩放,这里借鉴的是 multi-scale 思路,详见博士论文的 7.7 小节,目的是为了提高本算法的鲁棒性:
3. 计算中间变量 $\mathbf{G}$ 与 $\mathbf{h}$,存储到矩阵 M 中:
OpenCV 子函数 FarnebackUpdateFlow_GaussianBlur、FarnebackUpdateFlow_Blur
理论基础
根据光流的基本假设:光流的变化(向量场)几乎是光滑的。因此利用中间变量 $\mathbf{G}$ 与 $\mathbf{h}$ 求解光流场 $d_{out}$ 前,需要进行一次局部模糊化处理(主函数中
\mathbf{d}_{out}(\mathbf x)=\mathbf G_{avg}(\mathbf x)^{-1} \mathbf h_{avg}(\mathbf x)
源码解读
-
根据中间变量的元素,计算得到光流场存储于 flow 数组。flow 数组也是主函数最后的输出量:
2. 因为模糊化操作可能会执行多次,需要调用子函数 FarnebackUpdateMatrices 更新中间变量矩阵 M:
函数使用举例
以上代码的运行效果截图为: