matlab练习程序（meanshift图像聚类）

　　关于这个meanshift，一来可以用来作为目标跟踪，二来可以用来进行图像聚类。我这里只实现了图像聚类，当然，是按自己的理解编写的程序。至于目标跟踪将来一定也是要实现的，因为我最初看这个算法的原因就是想用他来跟踪目标的。

　　meanshift的基本原理我就不介绍了，比起我的介绍，网上有不少牛人们比我解释的好，最后我会列出我参考的文章。我这里说一下我是怎么理解meanshift图像聚类的。这里的聚类也像过去的滤波一样，需要一个模板矩阵，不过这个模板不是事先设置好的矩阵，而是在当前处理的像素周围提取一个r*r的矩阵，然后把这个矩阵化为一维向量，再对这个向量进行meanshift，最终迭代到的值再赋值给当前处理的像素。所以可以这样理解，把图像经过meanshift迭代到相同值的像素聚为一类。

　　我这里使用的是灰度图像，至于彩色图像，我看到一篇博客上把rgb域转换到luv域上再去做处理，这个我就不太清楚了，不过我看他的代码其中有一部分很像均值滤波。虽然我没有和他用一样的方法，不过他的代码也可以参考一下。传送门在此。

　　下面是代码（这都是我自己的理解，不能保证都正确，不过至少可以为你的编码提供一些思路）：

main.m

clear all;

close all;

clc;



r=2;        %滤波半径

img=imread('lena.jpg');

imshow(img);

img=double(img);

[m n]=size(img);



imgn=zeros(m+2*r+1,n+2*r+1);



imgn(r+1:m+r,r+1:n+r)=img;

imgn(1:r,r+1:n+r)=img(1:r,1:n); 

imgn(1:m+r,n+r+1:n+2*r+1)=imgn(1:m+r,n:n+r);

imgn(m+r+1:m+2*r+1,r+1:n+2*r+1)=imgn(m:m+r,r+1:n+2*r+1);

imgn(1:m+2*r+1,1:r)=imgn(1:m+2*r+1,r+1:2*r);

imshow(mat2gray(imgn))



for i=1+r:m+r

    for j=1+r:n+r

        ser=imgn(i-r:i+r,j-r:j+r);

        ser=reshape(ser,[1 (2*r+1)^2]);         %将二维模板变为一维

        imgn(i,j)=mean_shift(ser,2*r^2+2*r+1);   %取模板最中间的那个值作为迭代初值

    

    end    

end



figure;

imgn=imgn(r+1:m+r,r+1:n+r);

imshow(mat2gray(imgn));

meanshift.m

function   re= mean_shift( ser,p)

    [m n]=size(ser);

    tmp=double(ser);



    pre_w=tmp(p);

    point=p;

    while 1

        ser=tmp-pre_w;



        for i=1:m*n

            if i ~= point

                ser(i)=ser(i)/(i-point);            %i-point是距离，就是各种公式里的h

            end

        end



        ser=ser.^2;

        K=(1/sqrt(2*pi))*exp(-0.5*ser);         %传说中的核函数

        w=sum(tmp.*(K))/sum(K);



        if abs(w-pre_w)<0.01

            break;

        end

        pre_w=w; 

    end

 %   tmp1=abs(tmp-w);

 %   [i point]=min(tmp1);

    re=w;

 %   if max(tmp)-w<0.01

 %       point=0;

 %   end

 %   point=w;

end

处理的效果：

原图

半径为2处理的效果

——————————下面是2013.5.30添加————————————

上一部分的meanshift图像聚类还需修改，下面实现最简单的meanshift算法，完全按照原理来。

最后的参考文献都是很好的总结，不过这次我是参考的《图像处理、分析与机器视觉（第3版）》这本书。

下面是通常所见的迭代效果：

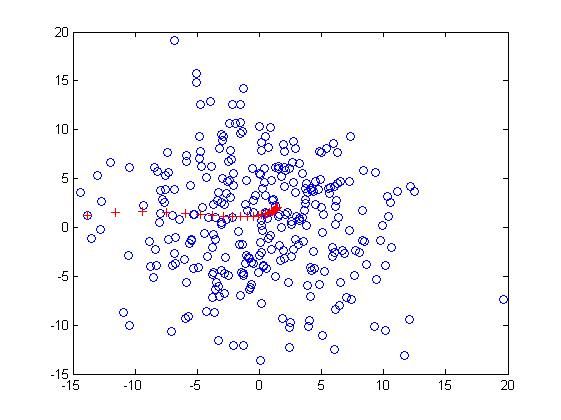
程序如下：

clear all; close all; clc;



%测试数据

mu=[0 0];  %均值

S=[30 0;0 35];  %协方差

data=mvnrnd(mu,S,300);   %产生300个高斯分布数据

plot(data(:,1),data(:,2),'o');



h=3;    %核的大小

x=[data(1,1) data(1,2)];    %以第一个数据为迭代初值

pre_x=[0 0];



hold on

while norm(pre_x-x)>0.01;

    

    pre_x=x;

    plot(x(1),x(2),'r+');

    u=0;        %分子累加项

    d=0;        %分母累加项

    for i=1:300

        %最关键的两步，均值位移公式实现

        k=norm((x-data(i,:))/h).^2;        

        g=(1/sqrt(2*pi))*exp(-0.5*k);

        

        u=data(i,:)*g+u;

        d=g+d;

    end

    M=u/d;      %迭代后的坐标位置

    x=M;

 

end

 

参考：

1.http://en.wikipedia.org/wiki/Mean-shift wiki百科，介绍的简介明了。

2.http://www.cnblogs.com/liqizhou/archive/2012/05/12/2497220.html 非常详细的理解。

3.http://emuch.net/bbs/viewthread.php?tid=4626864 小木虫上一个同学的理解。

4.http://en.wikipedia.org/wiki/Kernel_(statistics) 介绍核函数的。

5.http://wenku.baidu.com/view/11b6a7de6f1aff00bed51eac.html 提出meanshift算法的论文，虽然我没怎么看，不过想对算法彻底理解的还是看这篇好。