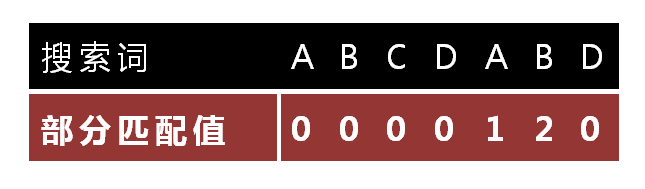九章算法基础班1.Introducing Algorithm Interview & Coding Style

第一题 Leecode 28. Implement strStr()

传送门：https://leetcode.com/problems/implement-strstr/description/

1. 我们先来暴力解，上下两个单词挨个字母比较n方复杂度看看情况
2. KMP，这个是n的复杂度，高大上，我们一会儿在看

1. 暴力解：

思路简单粗暴，但是AC了也，毕竟n方也还算可以。这个题目，基本思路就是两个指针，一个pointer i 指向haystack，一个 pointer j 指向needle。一个一开始遍历：i 上的char和j上的char一样的时候，两个指针分别+1往下走。如果不一样了，指针i 向前移动，到i - j + 1 的位置，j恢复为0。回到最初的起点，呆呆地站在镜子前。

class Solution {
    public int strStr(String haystack, String needle) {
        if(needle.length() == 0){
            return 0;
        }
        int result = -1;
        int m = haystack.length();
        int n = needle.length();
        if(n > m){
            return result;
        }
        
        int i=0;
        int j=0;
        while(i < m && j < n){
            if(haystack.charAt(i) == needle.charAt(j)){
                i++;
                j++;
            }else{
                i = i - j + 1;
                j = 0;
            }
        }
        if(j == n){
            result = i - j;
        }
        return result;
    }
}

没能一次过，原因竟然是，if(j == n) 最后一个if判断， j == n = 1 了。。。忘了j自增。

2. KMP:

俗称，看毛片算法。哈哈哈。"word" W 中找到 "text string" S
KMP核心思想：当发生不匹配的时候，W中包含了让我们知道下一个匹配起点的全部信息， 因此我们不需要再匹配已经匹配过的字符，减少重复工作。
这样看不太懂，我们举个栗子：
Haystack:
0 1 2 3 4 5 6 7 8 9
o o h e l l h e l i
Needle:
0 1 2 3
h e l i

如果根据我们上面暴力解的做法，hel配过了，此时i 指针是5， j指针是3， 发现 l 和 i并不一样，然后我们回到最初的起点，大不了从头再来了。。。i 变成 i - j + 1 = 3, j变成0.
ellheli
heli
我们已经知道ell和heli不匹配了之前，那为什么要费尽再来一遍呢？
i不需要-j再往后移1格了，可以多移动一点儿嘛。

而当匹配另一种字符串的时候，也就是Haystack前缀和后缀一样，如果Needle匹配了一样前缀的之后不匹配了，那我们就知道needle的前缀肯定是匹配得上Haystack目前的后缀的。比过的就不用再比了。

这段解释wiki上真的写的太好了，大家去附录wiki里看 https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
wiki里有所有匹配情况的栗子，
一个字母都匹配不上的：i+1，j归零；
匹配了一半匹配不上的：
needle前缀如果和haystack前缀不一样：
i+j-1， j归零
needle前缀如果和haystack前缀一样：
i设置成最后一个不匹配的index，j则为前后缀相等的下一个数。

伪代码上线：
歌词大意看完，我们来点儿干货，看看伪代码。你也许已经注意到了，这个KMP关键在于有个前缀后缀匹配，这个跟我们straight forward的暴力思路不一样，不能一眼看出来匹配，所以需要个中间数组来存些东西，也就是匹配信息。好多题目，数组题目，的高级解法都是搞个中间数组。

友情提示，在看下面一段文字之前，去wiki上看例子，不然将会十分抽象！在一下的描述中，我们S是那个厂的数组，W是短的那个，需要在S中找到W。

现在，我们假设有个partial match table T，这个T是啥呢，是在目前mismatch的地方，下一个新match开始的起点。先甭管T是咋来的，下面我们会给T开个段落具体讲，T现在就是天上飞来的，拯救我们的一个array。T里的每个entry物理意义是：假设我们match开始于S[m], 然后S[m+i]和W[i]的时候mismatch了，那么下一个可能的match开始于S中的m+i-T[i]。换句话说，T[i]是mismatch之后，我们回退了几格。由于我们不想重复以前match过的字母给我们的讯息，不想像第一种暴力解法里面，每次失败了都从m+1开始从头来过，我们就需要研究mismatch之后，最少可以退几格。

T数组的物理意义明确了，间接告诉我们两点：第一，T[0] = -1，i=0的时候不match，W[0]第一个字母就没match上，也就是S[m]没match上，我们一格也不能退，必须顺着查看下一个字母。第二一个，尽管下一个可能的match开始于index m+i-T[i]，但是我们知道T[i]这个回退了几格的字母是已经match好的了，就是说S中断后面T[i]个字母，和W中前面T[i]个字母已经match了，我们从W[T[i]]开始找match就行了。
上伪代码：

algorithm kmp_search:
    input:
        an array of characters, S (the text to be searched)
        an array of characters, W (the word sought)
    output:
        an array of integers, P (positions in S at which W is found)
        an integer, nP (number of positions)

    define variables:
        an integer, j ← 0 (the position of the current character in S)
        an integer, k ← 0 (the position of the current character in W)
        an array of integers, T (the table, computed elsewhere)

    let nP ← 0

    while j < length(S) do
        if W[k] = S[j] then
            let j ← j + 1
            let k ← k + 1
            if k = length(W) then
                (occurrence found, if only first occurrence is needed, m may be returned here)
                let P[nP] ← j - k, nP ← nP + 1
                let k ← T[k] (T[length(W)] can't be -1)
        else
            let k ← T[k]
            if k < 0 then
                let j ← j + 1
                let k ← k + 1

wiki上贴过来的，已经自己解释自己解释的挺好了。唯一一点儿不清楚的就是那个nP，nP啊，就是所有W在S中出现的起始位置的集合。我们这里题目要求一个，遇到直接返回就行，nP不用。

在探究神奇的T table之前，我们来分析下这个目前的程序的复杂度。 假设T表已经存在，我们上面这个伪代码的复杂度是O(n)，n是S的长度。这个程序在while中进行，while是while的S的长度，n。整个过程中，j都在不断地增加。while里只有两个branch，上一个branch，每次匹配j都增加，没什么说的。第二个branch，m每次加上i-T[i], i是匹配上的字符的个数，所以i-T[i]一定大于0。

Partial match table 又叫做failure function，或者跳跃表。我们神秘的T隆重出场了。这个跳跃表，有两种起始条件的形式，第一种是-1 base的，第二种是0based。网上-1based的多一些，例如wiki，但是我看不懂。0based更符合我的理解。 wiki上的table真的是解释的无法吐槽，怎么看都看不懂，我需要狗都能看懂的解释，狗都能的那种啊！这个wiki不推荐真心。B站小哥讲的挺清楚的，KMP中文解释也不错。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

W = [A, B, C, D, A, B, D]

W的跳跃表

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

附录
有用的链接，也是一个九章的笔记： https://stomachache007.wordpress.com/2017/03/07/414/。
KMP 中文解释的好的，0based阮一峰老师： http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
KMP wiki： https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
KMP 另一篇中文： http://www.matrix67.com/blog/archives/115
B站中英字幕印度小哥讲解：https://www.bilibili.com/video/av3246487/
-1based解释很清楚的：
https://blog.csdn.net/shengchaohua163/article/details/77141025