使用numpy实现两层神经网络 (附Backward详细推导)

使用numpy实现两层神经网络 (附Backward详细推导)

基于numpy与pytorch

首先看看最简单的两层神经网络长的是什么样子的,如下,只有一个隐藏层

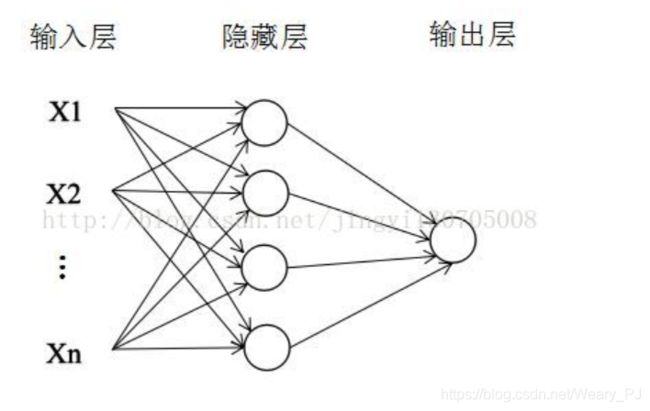
本次案例中只使用relu激活函数,也就是如下的结构

---

• $h=w_1\ast x$
• $h_{relu}=relu(h)$
• $\hat{y}=w_2\ast h_{relu}$

---

下面就来实现一下这个非常简单的神经网络
大致流程如下

• forward pass
• loss
• backward pass

numpy实现两层神经网络

这里就用随机数定义一些值作为输入,在实际情况可以读取文件信息等等

• N 代表 一共64个输入
• D_in 代表输入的维度数
• H 代表隐藏层的维度数
• D_out 代表输出的维度数

import numpy as np
import torch
N, D_in, H, D_out = 64, 1000, 100, 10
# N 代表 一共64个输入
# D_in 代表输入的维度数
# H 代表隐藏层的维度数
# D_out 代表输出的维度数

# 随机创建一些训练数据
x = np.random.randn(N, D_in) # 输入的训练数据 N * D_in
y = np.random.randn(N, D_out) # 输出的预测数据 N * D_out

w1 = np.random.randn(D_in, H) # 权重 w1 为 D_in * H  则 w1 * x => 结果为 N * H
w2 = np.random.randn(H, D_out) # 权重 w2 为 H * D_out 因为 relu操作不改变维度数, 所以输出的 w2 * relu(w1 * x ) => N * D_out

learning_rate = 1e-6 # 学习率

也就是说 输入的维度是 N * D_in 输出的维度是N * D_out
中间包含一个维度为H的隐藏层,而我们要训练的参数只有2个 w1和w2

forward

前向传播,这是最简单的
注意这里的 dot代表矩阵运算,也就是$a_{m\ast n}\ast b_{n\ast k}=结{果}_{m\ast k}$

 # Forward pass 
    # 这里的.dot是矩阵运算 
    h = x.dot(w1) # N * H 计算出 第一层 w1 * x 的结果 h = w1*x
    h_relu = np.maximum(h, 0) # N * H 对于h做激活 h_relu = relu(h) 不改变维度 relu函数的作用是 小于0的都为0,大于0的不变
    y_pred = h_relu.dot(w2) # N * D_out 预测输出值 

loss

计算损失函数,也非常好理解
$$loss=(\hat{y}-y{)}^2$$
这里做的就是把它们累加起来,并且输出一下查看结果
有时候我们采用的是平均的方法,不过这里用的是sum

 # compute loss
    loss = np.square(y_pred - y).sum() # 计算损失,这里的损失函数为 loss = (y_pre - y ) ^ 2 
    print(epoch, loss)

Backward pass

这一步可能会稍微复杂一点,也就是计算梯度
而这里的梯度是一层一层往前传的,需要通过链式法则乘起来
目标是计算如下两个式子
$$\frac{dloss}{d{w}_1}$$
$$\frac{dloss}{d{w}_2}$$
我们先回顾一个整个的网络结构

---

• $h=w_1\ast x$
• $h_{relu}=relu(h)$
• $\hat{y}=w_2\ast h_{relu}$

---

而$loss=(\hat{y}-y{)}^2$
所以很显然
$$\frac{dloss}{d{w}_1}=\frac{dloss}{d\hat{y}}\ast \frac{d\hat{y}}{d{w}_1}$$
$$\frac{d\hat{y}}{d{w}_1}=\frac{d\hat{y}}{d{h}_{relu}}\ast \frac{d{h}_{relu}}{d{w}_1}$$
$$\frac{d{h}_{relu}}{d{w}_1}=\frac{d{h}_{relu}}{d_h}\ast \frac{d_h}{d{w}_1}$$
$$\frac{d_h}{d{w}_1}=x$$
而对于w2
$$\frac{dloss}{d{w}_2}=\frac{dloss}{d\hat{y}}\ast \frac{d\hat{y}}{d{w}_2}$$
$$\frac{d\hat{y}}{d{w}_2}=h_{relu}$$

下面我们就一步步的结合代码来计算

w1的梯度

先计算对于w1的
$$grad\_y\_pred=\frac{dloss}{d\hat{y}}$$

 grad_y_pred = 2.0 * (y_pred - y) # dloss / dy_pre = 2 * (y_pre - y) 

$$grad\_h\_relu=\frac{dloss}{d{h}_{relu}}=\frac{dloss}{d\hat{y}}\ast \frac{d\hat{y}}{d{h}_{relu}}(w_2)$$

grad_h_relu = grad_y_pred.dot(w2.T) 

因为relu函数求导,大于0的都为1,小于0的都为0
$$grad\_h=\frac{dloss}{d_h}=\frac{dloss}{d_{relu}}(grad\_h\_relu)\ast \frac{d{h}_{relu}}{d_h}(小于0的为0,大于0的为1)$$

grad_h = grad_h_relu.copy()
grad_h[h<0] = 0

$$grad\_w1=\frac{dloss}{d{w}_1}=grad\_h\ast \frac{dh}{d{w}_1}(x)$$

grad_w1 = x.T.dot(grad_h)

---

w2的梯度

$$\frac{dloss}{d{w}_2}=\frac{dloss}{d\hat{y}}(grad\_y\_pred)\ast \frac{d\hat{y}}{d{w}_2}(h\_relu)$$

grad_w2 = h_relu.T.dot(grad_y_pred)

更新权重

这步就很简单了,对于权重进行更新

# update weights of w1 and w2
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2

全代码

代码如下

import matplotlib.pyplot as plt
%pylab inline 
for epoch in range(500):
    # Forward pass 
    # 这里的.dot是矩阵运算 
    h = x.dot(w1) # N * H 计算出 第一层 w1 * x 的结果 h = w1*x
    h_relu = np.maximum(h, 0) # N * H 对于h做激活 h_relu = relu(h) 不改变维度 relu函数的作用是 小于0的都为0,大于0的不变
    y_pred = h_relu.dot(w2) # N * D_out 预测输出值 
    
    # compute loss
    loss = np.square(y_pred - y).sum() # 计算损失,这里的损失函数为 loss = (y_pre - y ) ^ 2 
    print(epoch, loss)
    
    # Backward pass
    # compute the gradient 下面就是一步步计算梯度,也可以认为是导数
    grad_y_pred = 2.0 * (y_pred - y) # dloss / dy_pre = 2 * (y_pre - y) 
    grad_w2 = h_relu.T.dot(grad_y_pred)
    grad_h_relu = grad_y_pred.dot(w2.T) 
    grad_h = grad_h_relu.copy()
    grad_h[h<0] = 0
    grad_w1 = x.T.dot(grad_h)
    
    # update weights of w1 and w2
    w1 -= learning_rate * grad_w1
    w2 -= learning_rate * grad_w2

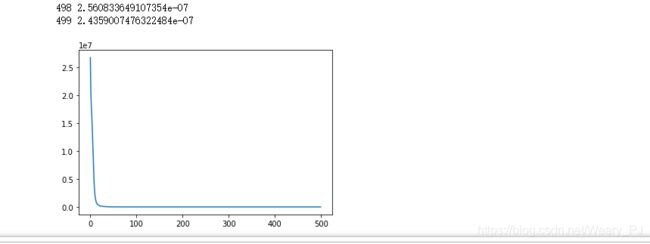
看看实现的结果

说明训练的结果还是比较成功的