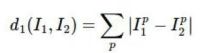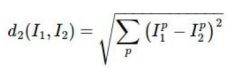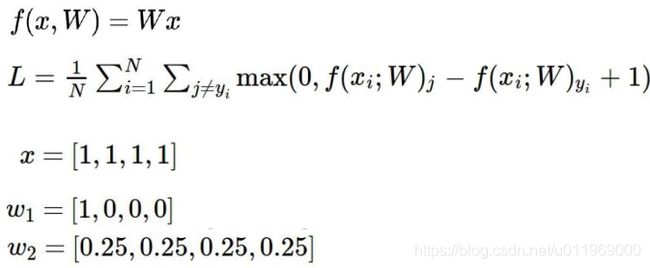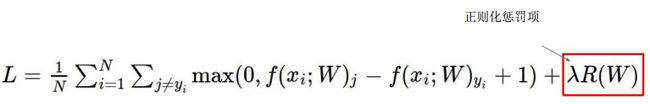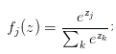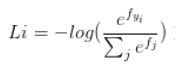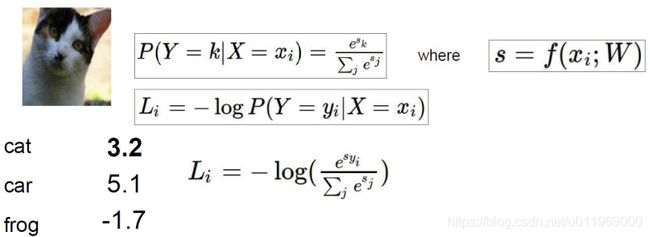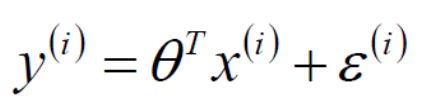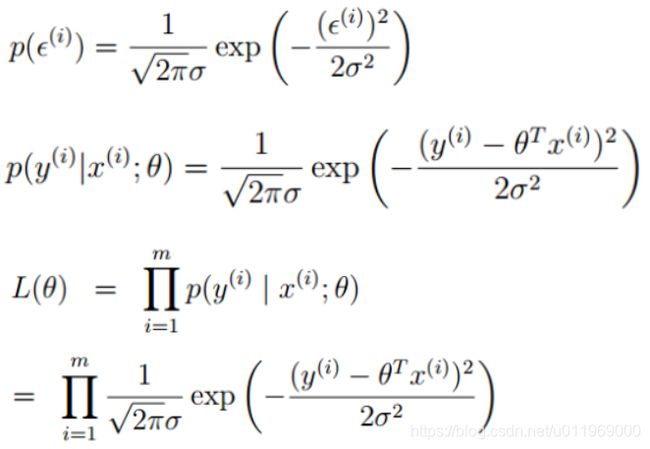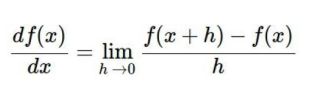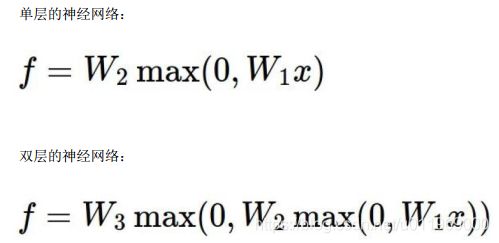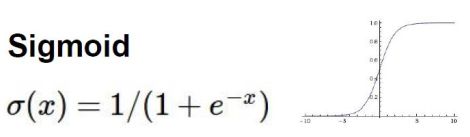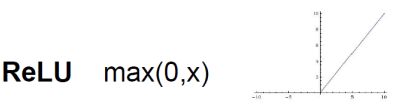深度学习入门（上）01（用cifar数据实现三层网络实现图片分类）

目录

1-1深度学习入门-imagenet图像分类比赛

1-2计算机视觉面临的挑战和常规套路

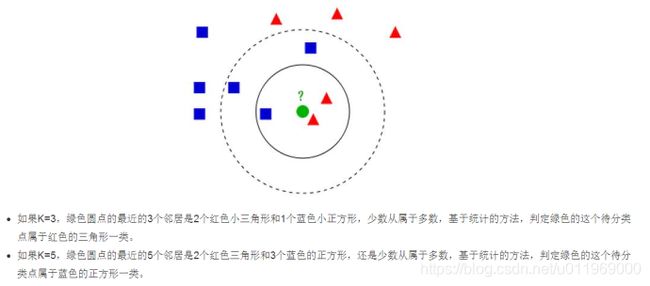
1-3 K近邻进行图像分类

KNN的实现步骤

KNN总结

KNN的问题：

数据库样例：

测试结果

最近邻实现代码

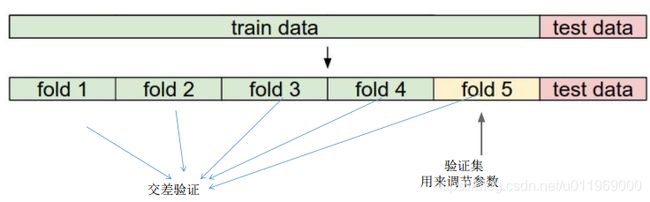
1-4 超参数与交叉验证

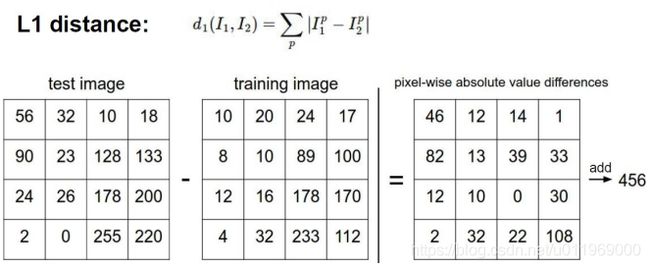
L1 manhanttan距离

L2 euclidean欧式距离

超参数的问题：

找到最好的参数

测试结果

结论：K近邻用于图像计算不可取

KNN方法用于图像识别总结

KNN方法用于图像识别步骤

1-5 线性分类

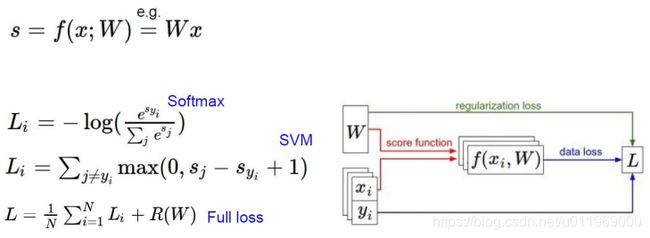
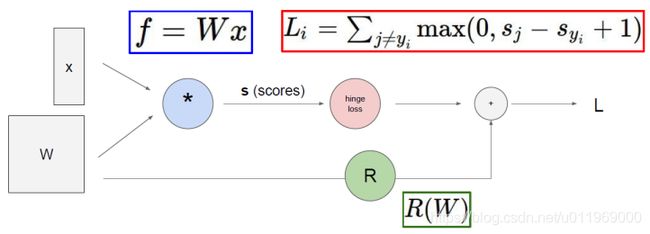
1-6 损失函数

 1-7正则化惩罚项

对比W1和W2两种权重模型的效果

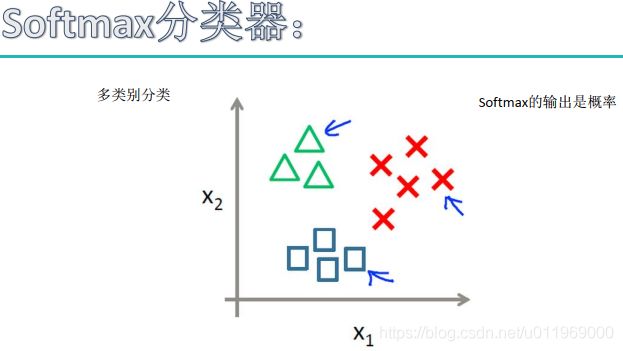
1-8 softmax分类器

svm和softmax两种损失函数对比

 1-9最优化形象解读

1-10 梯度下降算法原理

1-11 反向传播

2-1神经网络整体架构

神经网络结构：

激活函数

2-2神经网络模型实例演示

2-3 过拟合问题解决方案

神经网络整体流程;

数据预处理

权重初始化

DROP-OUT

3-1python环境搭建

3-2 eclipse 搭建python环境，选择IDE

3-3 深度学习入门

 3-5 神经网络案例-cifar分类任务

cifar数据集

3-6 神经网络案例-分模块构造神经网络

 3-7 神经网络案例-训练神经网络完成

---

cifar-10 dataset

数据集http://www.cs.toronto.edu/~kriz/cifar.html

1-1深度学习入门-imagenet图像分类比赛

官网http://www.image-net.org/

数据集介绍https://blog.csdn.net/fengbingchun/article/details/88606621

2012年alexnet卷积神经网络

百度人工智能实验室

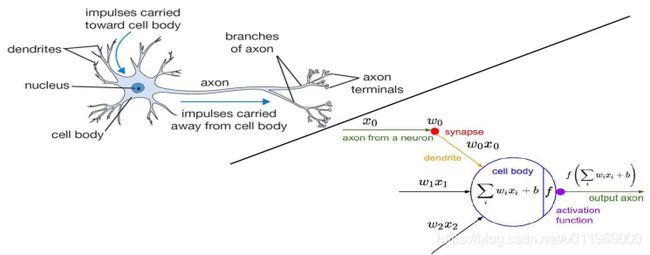
深度学习使用的神经网络是机器学习算法的分支

1-2计算机视觉面临的挑战和常规套路

图像分类

一张图片被表示成三维数组的形式，每个像素的值从0到255（像素点越大亮度越高），300*100*3：长宽颜色通道EGB

图像识别的挑战：照射角度，光照强度，形状改变，部分遮蔽，背景混入

常规套路

1、收集数据并给定标签

2、训练一个分类器

3、测试，评估

1-3 K近邻进行图像分类

Knn原理

KNN的实现步骤

对于未知类别属性数据集中的点，

1、计算已知类别数据集中的点与当前点的距离

2、按照距离一次排序

3、选取与当前距离最小的K个点

4、确定前K个点所在的类别的出现概率

5、返回前K个点出现频率最高的类别作为当前点预测分类

KNN总结

knn算法本身简单有效，是一种lazy-learning算法

分类器不需要训练数据集，训练时间复杂度为0，

knn分类的计算复杂度和训练集中的文档数目成正比，训练集中文档总数为n，那么KNN的分类时间复杂度为o(n)

KNN三要素：k值选择，距离度量和分类决策规则

KNN的问题：

该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很

小时，有可能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数

解决：不同的样本给予不同权重项

 

数据库样例：

CIFAR-10

10类标签，（airplane，automobile，bird，cat，deer，dog，frog，hurse，ship，truck）

50000个训练数据，10000个测试数据，大小均为32*32

 

如何计算：

用k近邻来进行图像分类，即为对图像像素点的计算，

测试结果

最近邻实现代码

import numpy as np
#KNN实现代码
class NearestNeighbor:
    def __init__(self):
        pass
    def train(self, X, y):
        #记录所有的训练数据，X=N*D Y=种类数
        self.Xtr = X
        self.ytr = y
    def predict(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test, dtype= self.ytr.dtype)
        #对于每一个测试数据找到与其l1举例最小的样本的标签作为它的标签
        for i in range(num_test):
            distances = np.sum(np.abs(self.Xtr - X[i, :]),axis = 1)
            min_index = np.argmin(distances)
            Ypred[i] = self.ytr[min_index]
        return Ypred

1-4 超参数与交叉验证

超参数，就是在训练中可以改变的参数，比如knn中的距离计算公式

L1 manhanttan距离

L2 euclidean欧式距离

超参数的问题：

1、距离如何设定

2、knn中的k如何设定

3、其他超参数如何设定

找到最好的参数

Train_data 70%，test_data 30%

多次用测试数据试验，找到做好的一组参数组合？

错误的的想法，测试数据只能最终用

测试集只能在最终使用

交叉验证70%的train_data里面切割为n个fold，其中一个为验证集

1，2，3，4→5

5，2，3，4→1

1，5，3，4→2

1，2，5，4→3

1，2，3，5→4

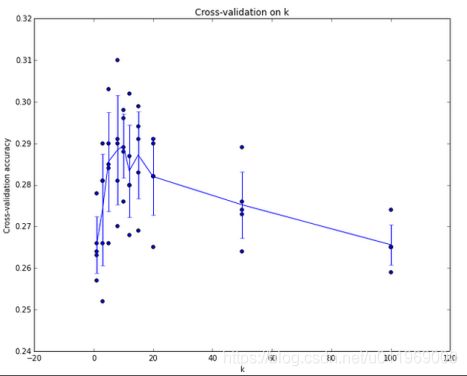
测试结果

x轴为k的大小，y轴为交叉验证准确率

结论：K近邻用于图像计算不可取

1、背景主导：knn在计算距离的时候，由于图中识别的物体只占少部分，把背景考虑进来了

2、不同的变换（偏离，遮挡，灰度）和原图具有相同的L2距离

KNN方法用于图像识别总结

1.选取超参数的正确方法是：将原始训练集分为训练集和验证集，我们在验证集上尝试不同的超参数，最后保留表现最好那个

2.如果训练数据量不够，使用交叉验证方法，它能帮助我们在选取最优超参数的时候减少噪音。

3.一旦找到最优的超参数，就让算法以该参数在测试集跑且只跑一次，并根据测试结果评价算法。

4.最近邻分类器能够在CIFAR-10上得到将近40%的准确率。该算法简单易实现，但需要存储所有训练数据，并且在测试的时候过于耗费计算能力

5.最后，我们知道了仅仅使用L1和L2范数来进行像素比较是不够的，图像更多的是按照背景和颜色被分类，而不是语义主体分身

KNN方法用于图像识别步骤

1.预处理你的数据：对你数据中的特征进行归一化（normalize），让其具有零平均值（zero mean）和单位方差（unit variance） 。

2.如果数据是高维数据，考虑使用降维方法，比如PCA

3.将数据随机分入训练集和验证集。按照一般规律， 70%-90% 数据作为训练集

4.在验证集上调优，尝试足够多的k值，尝试L1和L2两种范数计算方式。

发现不同的变换和原图具有相同的L2距离故K近邻不能用于图像识别

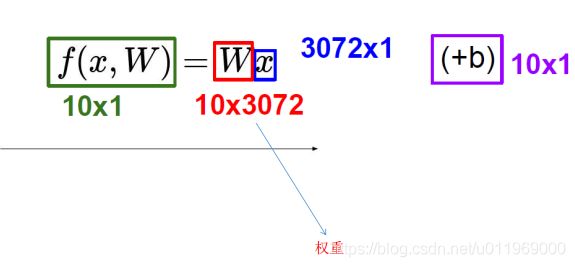
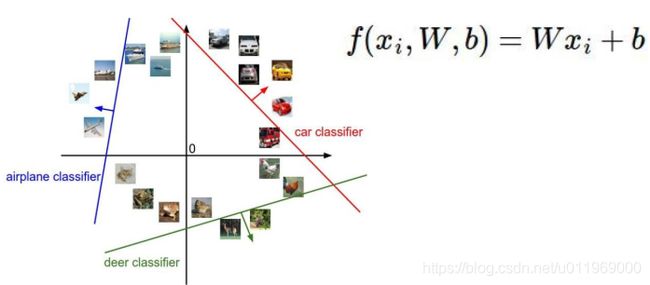
1-5 线性分类

 

输入x：32*32*3个像素点，W权重矩阵，b截距

输出b：10个类别的得分概率

得分值高位最终的结果值

线性分类，是按线性划分区域

出现预测错了，则需要改正

 

1-6 损失函数

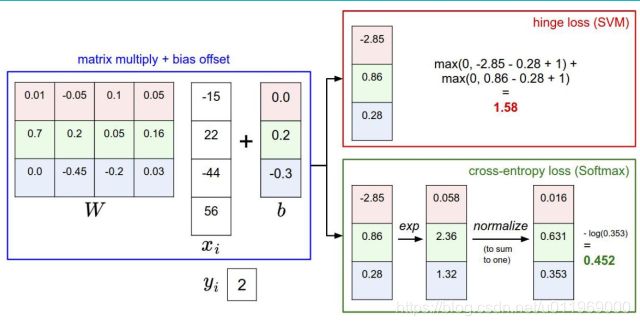
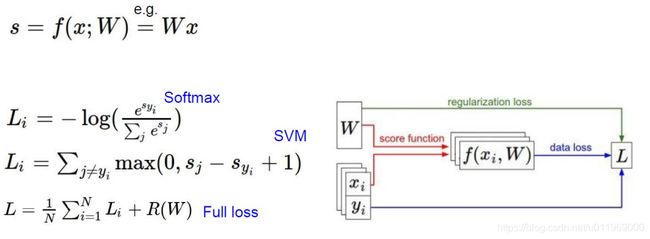
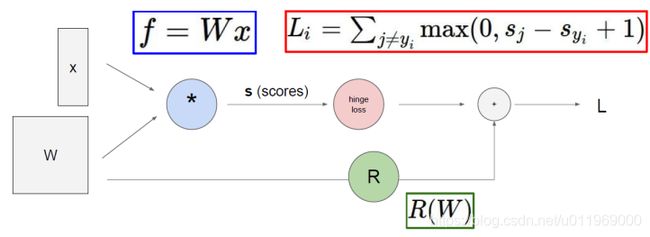
SVM损失函数

Sj是其他J个类别的概率，Syi准确的类别的概率

+1（delta）：可容忍程度，偏离的大小小于1则不计

<0的损失不计入。>0计入算是

 1-7正则化惩罚项

对比W1和W2两种权重模型的效果

W1的权重至考虑x1这个像素点，其他3个像素点可以为任何职，W2在像素点的权重比较均匀，惩罚项小

为了选到W2这样的权重，原始损失函数需加上正则化惩罚项，惩罚项惩罚权重参数

R(W)用来l2正则化

L1=1>L2=1/4,L1惩罚得比较多

SVM损失函数终极版

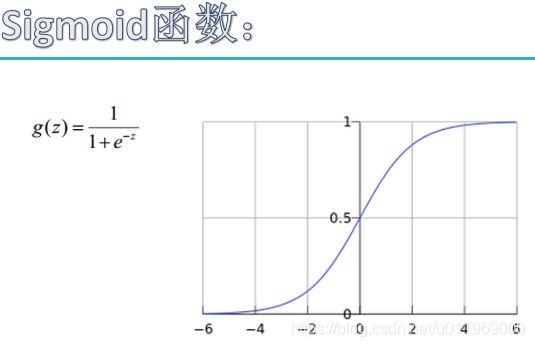
1-8 softmax分类器

 

sigmoid把任意实数变成0-1的概率值

softmax函数

softmax分类器的作用

softmax的输出，是归一化的分类概率

损失函数（交叉熵损失，cross-entropy loss）

 

输入：一个向量，向量中元素为任意实数的评分值

输出：一个向量，每个元素值在0-1之间，且所有元素之和为1

示例：

 

eg：exp(3.2) ，归一化，-log()，

e的x次幂，如果是负数为变成很小的值，

归一化操作，概率值且和为1

拿cat的正确类别的损失值Li

svm和softmax两种损失函数对比

svm的损失函数，对错误类别的差异不大， 不用

一般用softmax函数计算损失函数

 

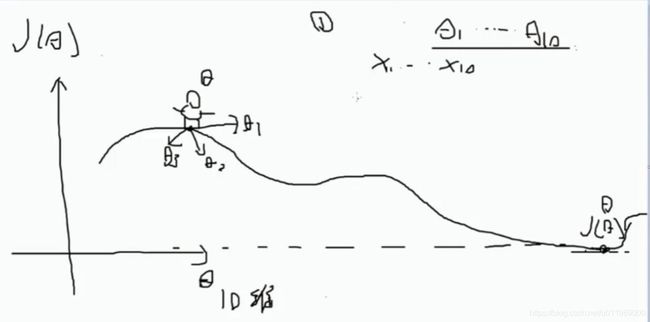
 1-9最优化形象解读

一步步喂数据，一步步优化θ参数，迭代优化的过程很重要

 

h(x)为线性回归公式

y为第i个参数的预测模型

 

根据误差的正态分布特性

 

J(θ)为待优化的建模函数

粗暴的方法代码实现及结果：

import numpy as np
#粗暴的想法，直接到山底
#X_trian为传入数据矩阵，如3073*50000
#y_train为图片的类别标签概率值，如10*50000
#假设L函数来估计损失函数
bestloss = float("inf")
for num in range(1000):
    W = np.random.randn(10, 3073) * 0.0001
    loss = L(X_trian, Y_train, W)
    if loss < bestloss:
        bestloss = loss 
        bestW = W
    print ('in attempt %d the loss was %f,best %f' %(num,loss,bestloss))
#粗暴想法的结果
#假设X_test是3073*10000，Y_test为10000*1
#scores为10*10000，每一类的分数矩阵
scores = Wbest.dot(Xte_cols)
#获取最高分的类别
Yte_prediect = np.argmax(scores ,axis = 0)
#计算平均预测准确精度
np.mean(Yte_predict == Yte)

m=10，沿着坡度下山最快，坡度为切线

跟随梯度函数

Bachsize通常是2的整数倍（32， 64， 128）2的整数次幂

#找打山坡最低点
#生成随机初始权重W
W = np.random.randn(10,3073)*0.001
bestloss = float("inf")
for i in range(1000):
    step_size = 0.0001
    Wtry = W + np.random.randn(10,3073) * step_size
    loss = L(Xtr_cols,Ytr,Wtry)
    if loss < bestloss:
        W = Wtry
        bestloss = loss
    print ('iter %d loss is %f') % (i ,bestloss)
#跟随梯度
def eval_numerical_gradient(f,x):
    fx = f(x)
    grad = np.zeros(x.shape)
    h = 0.00001
    it = np.nditer(x,flags=['multi_index'],op_flags = ['readwrite'])
    while not it.finished:
        #f(x+h)
        ix = it.multi_index
        old_value = x[ix]
        x[ix] = old_value + h #增加h
        fxh = f(x) #估计f(x+h)
        x[ix] = old_value
        grad[ix] = (fxh - fx) / h
        it.iternext()
    return grad
#梯度下降,bacthsize 通常是2的整数倍，32，64，128，256
while True:
    data_batch = sample_training_data(data, 256)
    weight_grad = evaluate_gradient(loss_fun, data_batch, weights)
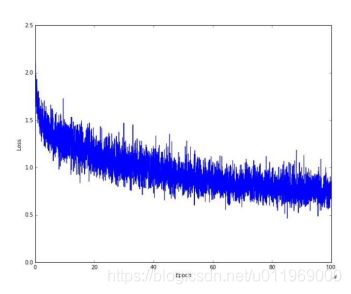
    weights += - step_size * weight_grad#学习步长*更新梯度

训练网络时，loss值的可视化结果

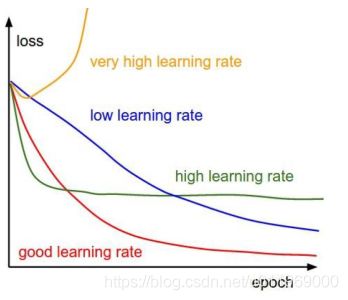
学习率：一次学习多大，△w多大，一般设置学习率设置为0.0001

通过小的学习率大的跌打次数进行训练

训练网络时的LOSS值视化结果

1-10 梯度下降算法原理

X 到loss 前向传播

BP算法是前向传播

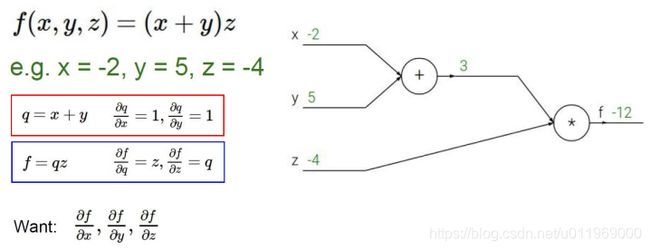
1-11 反向传播

最优化体现在反向传播

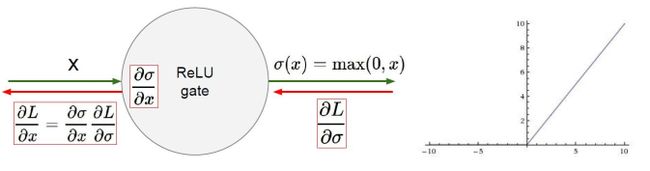
分别计算x,y,z对l的影响

把公式量化，量式法则

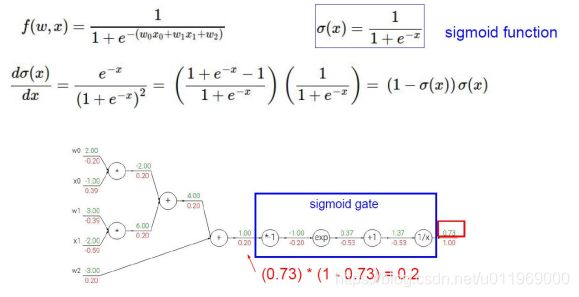
sigmoid函数的一步一步求导向前传

整体求导，先求sigmoid函数再求线性回归，

 

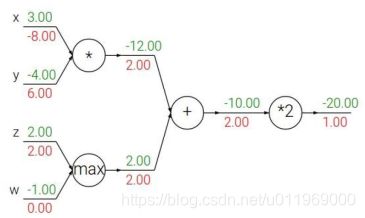
引入门单元

加法门单元：均等分配，求偏导都为1

MAX门单元：给最大的，把梯度分为较大的值，

乘法门单元：互换，q对x求偏导为y，对y求偏导为x梯度互换

 

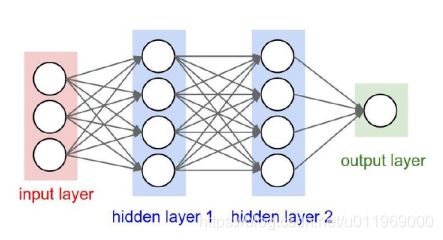
2-1神经网络整体架构

 

 

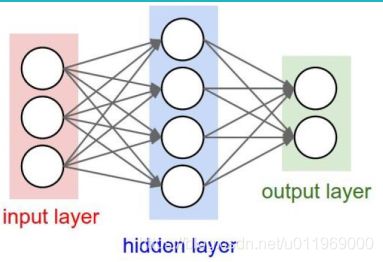
神经网络结构：

层次的结构（神经网络是由权重参数的组合构成）：

输入层（x1，x2，x3），隐藏层1（W1），隐藏层2（W1）和输出层out

隐藏层：权重的中间计算结果，第一层的权重系数，第二层，第n层

比如(W3(W2(W1*X1)))=OUT

神经网络必须指定的参数：Wx

为啥存在多个隐藏层Wx：隐藏层中包含激活函数，如下非线性中的Max()可视为激活函数

 

非线性方程中包含单层，多层

 

激活函数

因线性函数的分类能力不够，增加非线性函数加强模型能力，激活函数加强神经网络的效果

比如sigmoid函数吧线性压缩成非线性sigmoid(W1*x)

当取负无穷为0，正无穷为1，出现的问题：

正向传播，分步求导，每次梯度都要累乘，

sigmoid的导数为切线， 当值越大或越小，越接近0，出现梯度消失，

sigmoid被淘汰，因梯度消失太严重

引入RELU函数作为激活函数

X<0都为0，求导简单

 

2-2神经网络模型实例演示

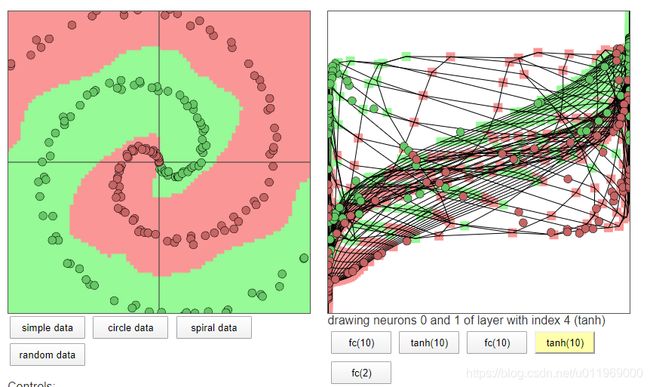
谷歌神经网络游乐园

http://playground.tensorflow.org/

斯坦福提供的一个用java-script写的2层隐藏层的训练网络

https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html

 

layer_defs = [];

layer_defs.push({type:'input', out_sx:1, out_sy:1, out_depth:2});

layer_defs.push({type:'fc', num_neurons:10, activation: 'tanh'});#设置隐藏层1

layer_defs.push({type:'fc', num_neurons:10, activation: 'tanh'});#设置隐藏层2

layer_defs.push({type:'softmax', num_classes:2});

 

net = new convnetjs.Net();

net.makeLayers(layer_defs);

 

trainer = new convnetjs.SGDTrainer(net, {learning_rate:0.01, momentum:0.1, batch_size:10, l2_decay:0.001});

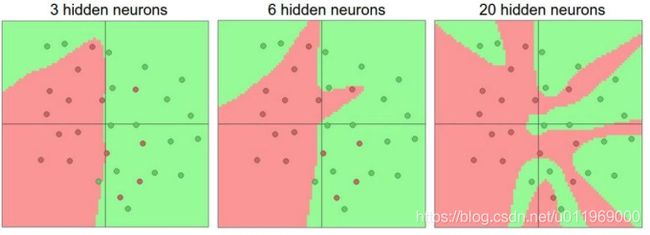
对于模型训练而言（比如环绕型数据），隐藏层设置越多，效果越好

神经网络层越多，过拟合现象越明显

 

2-3 过拟合问题解决方案

神经网络的特点：W1,W2无法解释

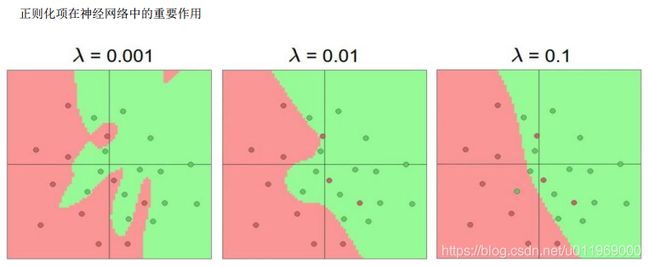
正则化的作用，λW^2

λ较小的时候，为了中间的红色，或拟合出一个圈，但实际测试数据分布来说，这个点为绿色的概率比较大，出现过拟合，部分错误点，异常点，离群点影响了结果

λ较大的时候，模型较平滑，泛化能力越强，

神经元越多，越能表达复杂的模型，但过拟合的危险越大

神经网络整体流程;

输入x0,x1,x2,经过w1,w2,w3组合之后，经过激活函数产生非线性模型效果

 

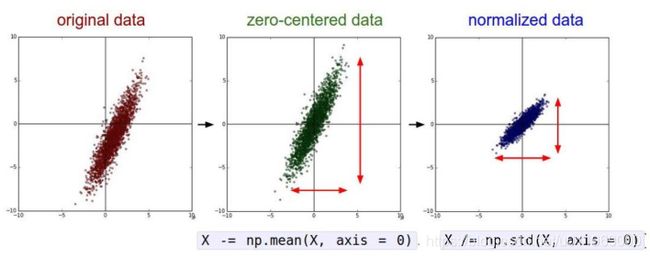
数据预处理

原始数据（0-255）→（均值为0）0为中心点数据→（除以标准差）归一化数据

权重初始化

初始值为0，训练不出来都是0

初始值方式：随机初始化，高斯初始化

随机初始化

W=0.0.1*np.random.randn(D,H)

对于b，0值或1值初始化。

 

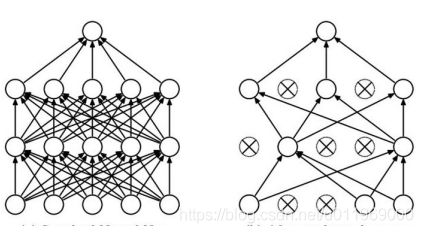
DROP-OUT

（左）全连接操作：每个神经元，每个x和w都连接，容易过拟合，

（右）drop-out：对于部分w1，w3，w4不用传播了，每次迭代，随机选择指定drop-out率为60%，只留下60%的神经元进行前向和反向传播，显得神经网络不那么臃肿，降低过拟合的风险，

目前的神经网络都会drop-out

 

3-1python环境搭建

1、下载python

2、配置系统环境变化

3、配置库

Numpy

用conda安装，或者pip安装

conda集成了python和python库

conda list

jupyter：可视化显示，debug麻烦

用ananconda查找适配的包机安装

ananconda search -t conda tensorflow

Ananconda show  dhirschfeld/tensorflow

conda install --channel https://conda.anaconda.org/Paddle paddlepaddle-gpu

conda install --channel https://pypi.tuna.tsinghua.edu.cn/simple paddlepaddle-gpu

3-2 eclipse 搭建python环境，选择IDE

选择自己舒服的环境，

eclipse一般用来写java，需要在java的环境运行，需要配置jdk，

下载python编译插件

Name:PyDev

Location:网站

配置IDE环境中的python编译器环境

新增interpreter

本实验用vscode

 

3-3 深度学习入门

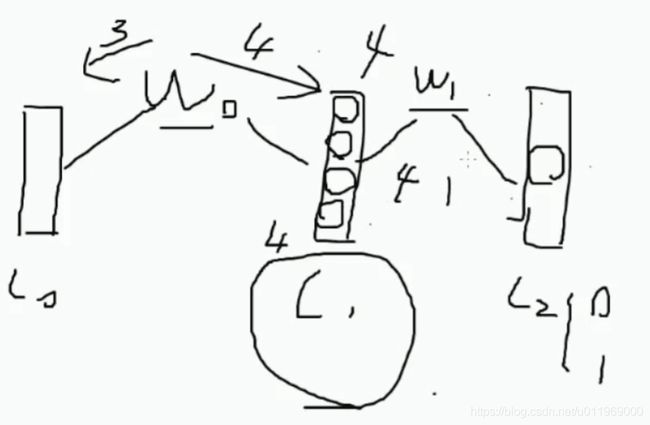
写一个只有三层的神经网络

X0在输入层L0

LI为隐藏层

L2输出层

import numpy as np
#定义激活函数，前后项传播都需要经历激活函数
def sigmoid(x,deriv = False):
    #判断是否需要激活,需要激活则返回导数，不需要则返回原公式
    if (deriv == True):
        return x*(1-x)
    return 1/(1+np.exp(-x))
#指定输入x值,y值
#构造5个数据，每个数据有3个特征
x = np.array([[0,0,1],[0,1,1],[1,0,1],[1,1,1,],[0,0,1]])
#查看数据维度
print(x.shape)
#构造label，y值
y = np.array([[0],[1],[1],[0],[0]])
print(y.shape)
#指定随机种子
np.random.seed(1)
#参数的初始化，l0，l1,
w0 = np.random.random((3,4))
w1 = np.random.random((4,1))
print(w0,"\n **************\n",w1)
#随机的取值在-1到1之间
w0 = 2 * np.random.random((3,4)) - 1
w1 = 2 * np.random.random((4,1)) - 1
print(w0,"\n **************\n",w1)
#三层前向传播
for j in range(5):
    l0 = x #输入层
    l1 = sigmoid(np.dot(l0, w0)) #中间层
    l2 = sigmoid(np.dot(l1, w1)) #输出层
    l2_error = y - l2 #均方误差的求导后公式
    #print(l2_error.shape)
    if (j%6000) == 0:
        print('error' +str(np.mean(np.abs(l2_error))))
    #向前传播，l2_error越大说明错得越多，越需要更新权重
    #每个样本错了多少
    l2_delta = l2_error * sigmoid(12,deriv=True) #对应位置相乘
    #print(l2_error.shape) #5*1
    #print(l2_delta.shape) #5*1
    #print(w1.shape) #4*1
    l1_error = l2_delta.dot(w1.T)
    l1_delta = l1_error * sigmoid(11,deriv=True) 
    #梯度更新参数权重，y-l2+=/l2-y-=/
    w1 += l1.T.dot(l2_delta)
    w0 += l0.T.dot(l1_delta)

目录 3-4感受神经网络的强大

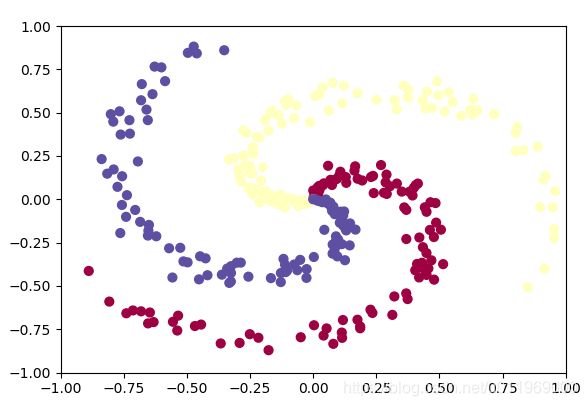
 运行drawData脚本，随机输出3类点，每类100个，做三分类任务

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
np.random.seed(0)
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D))
y = np.zeros(N*K, dtype='uint8')
for j in range(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
fig = plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim([-1,1])
plt.ylim([-1,1])
plt.show()

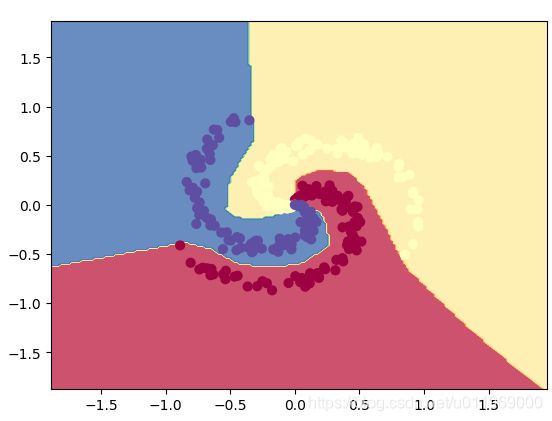
数据呈环状的分不规则，通过线性无法切开，

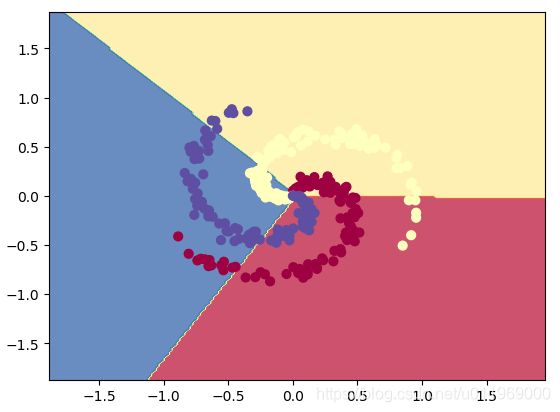
对比1：使用线性分类，运行linerCla.py

#Train a Linear Classifier
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D))
y = np.zeros(N*K, dtype='uint8')
for j in range(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
# 初始化W和b
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
# some hyperparameters，加入了正则化惩罚项
step_size = 1e-0
reg = 1e-3 # regularization strength
# gradient descent loop循环前后传播
num_examples = X.shape[0]
for i in range(1000):
  # evaluate class scores, [N x K]
  scores = np.dot(X, W) + b   #x:300*2 scores:300*3
  # compute the class probabilities，归一化操作
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K] probs:300*3
  #print(probs.shape) 
  # compute the loss: average cross-entropy loss and regularization，计算出loss准备向前传播
  corect_logprobs = -np.log(probs[range(num_examples),y]) #corect_logprobs:300*1
  #print (corect_logprobs.shape)
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 100 == 0:
    print ("iteration %d: loss %f" % (i, loss))
  
  # compute the gradient on scores,求解得出最好的模型参数
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)
  dW += reg*W # regularization gradient
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db
  scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print ('training accuracy: %.2f' % (np.mean(predicted_class == y)))
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

输出结果
(base) D:\DL\02>E:/anaconda3/python.exe d:/DL/02/3-4class3NN/linerCla.py
iteration 0: loss 1.096919
iteration 100: loss 0.787937
iteration 200: loss 0.786281
iteration 300: loss 0.786231
iteration 400: loss 0.786230
iteration 500: loss 0.786230
iteration 600: loss 0.786230
iteration 700: loss 0.786230
iteration 800: loss 0.786230
iteration 900: loss 0.786230
training accuracy: 0.49

结论：线性分类器的表达效果不那么好

对比2：使用非线性分类，运行NNCla.py

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D))
y = np.zeros(N*K, dtype='uint8')
for j in range(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
  
h = 100 # size of hidden layer,100个神经元
W = 0.01 * np.random.randn(D,h)# x:300*2  2*100
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))
# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength
# gradient descent loop
num_examples = X.shape[0]
for i in range(2000):
  # evaluate class scores, [N x K]
  hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation hidden_layer:300*100
  #print hidden_layer.shape
  scores = np.dot(hidden_layer, W2) + b2  #scores:300*3
  #print scores.shape
  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  #print probs.shape
  
  # compute the loss: average cross-entropy loss and regularization
  corect_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2)
  loss = data_loss + reg_loss
  if i % 100 == 0:
    print ("iteration %d: loss %f" % (i, loss))
  
  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters
  # first backprop into parameters W2 and b2
  dW2 = np.dot(hidden_layer.T, dscores)
  db2 = np.sum(dscores, axis=0, keepdims=True)
  # next backprop into hidden layer
  dhidden = np.dot(dscores, W2.T)
  # backprop the ReLU non-linearity
  dhidden[hidden_layer <= 0] = 0
  # finally into W,b
  dW = np.dot(X.T, dhidden)
  db = np.sum(dhidden, axis=0, keepdims=True)
  
  # add regularization gradient contribution
  dW2 += reg * W2
  dW += reg * W
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db
  W2 += -step_size * dW2
  b2 += -step_size * db2
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print ('training accuracy: %.2f' % (np.mean(predicted_class == y)))

h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.maximum(0, np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b), W2) + b2
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

(base) D:\DL\02>E:/anaconda3/python.exe d:/DL/02/3-4class3NN/NNCla.py
iteration 0: loss 1.098765
iteration 100: loss 0.723927
iteration 200: loss 0.697608
iteration 300: loss 0.587562
iteration 400: loss 0.426585
iteration 500: loss 0.357190
iteration 600: loss 0.349933
iteration 700: loss 0.346522
iteration 800: loss 0.336137
iteration 900: loss 0.309860
iteration 1000: loss 0.292278
iteration 1100: loss 0.284574
iteration 1200: loss 0.275849
iteration 1300: loss 0.271355
iteration 1400: loss 0.267756
iteration 1500: loss 0.265369
iteration 1600: loss 0.262948
iteration 1700: loss 0.260838
iteration 1800: loss 0.259226
iteration 1900: loss 0.257831
training accuracy: 0.97

结论：适合非线性数据，缺点过拟合

 3-5 神经网络案例-cifar分类任务

cifar数据集

The CIFAR-10 dataset consists of 60000 32x32 colour images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images.

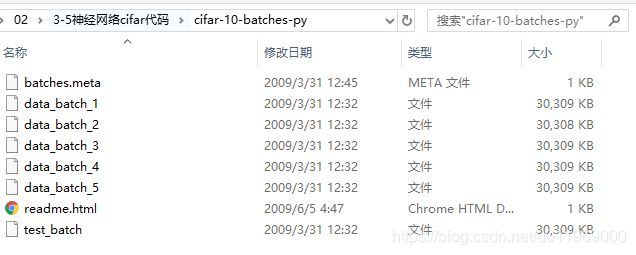
网页下载后，显示如下

有5个batch，每个batch里面有1万张图片，

代码测试数据，在batch1取了，5000张训练图像，500张测试图像

Data_utils.py的get_CIFAR10_data函数进行了数据初始化

def get_CIFAR10_data(num_training=5000, num_validation=500, num_test=500):

数据是4维，h，w，c，b一次输入多张图像，一个batch一个batch进行迭代

 

1、读入数据集，切分数据，5000张训练数据，500验证数据，500测试集

验证集找到w 和b，再测试出测试集的label

2，神经网络网络结构

输入层data

中间层l1 +relu激活函数

输出层，output，10类别

使用softmax得出p1,p2,,,p10的10个类别的概率值

得出loss值反向传播算出w1和w2

3、规范的分模块写代码

 

3-6 神经网络案例-分模块构造神经网络

 

 3-7 神经网络案例-训练神经网络完成

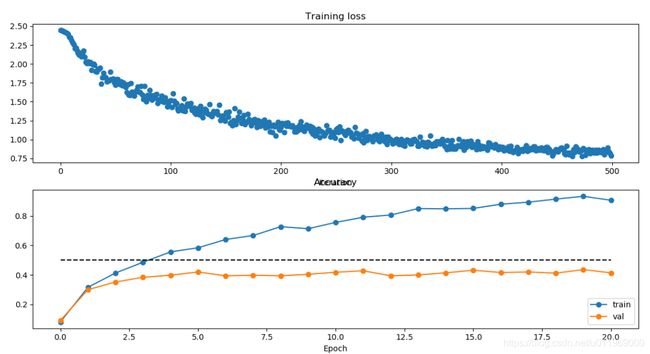
修改数据集路径，运行two_layer_fc_net_start.py

(tensorflow-gpu) D:\DL\02>E:/anaconda3/envs/tensorflow-gpu/python.exe d:/DL/02/3-5cifar-10-python/two_layer_fc_net_start.py
(10000, 32, 32, 3)
(Iteration 1 / 500) loss: 2.443408
(Epoch 0 / 40) train acc: 0.081000; val_acc: 0.092000
(Epoch 1 / 40) train acc: 0.316000; val_acc: 0.300000
(Epoch 2 / 40) train acc: 0.413000; val_acc: 0.352000
(Epoch 3 / 40) train acc: 0.486000; val_acc: 0.384000
(Epoch 4 / 40) train acc: 0.556000; val_acc: 0.398000
(Iteration 101 / 500) loss: 1.521124
(Epoch 5 / 40) train acc: 0.584000; val_acc: 0.420000
(Epoch 6 / 40) train acc: 0.640000; val_acc: 0.394000
(Epoch 7 / 40) train acc: 0.667000; val_acc: 0.398000
(Epoch 8 / 40) train acc: 0.727000; val_acc: 0.394000
(Iteration 201 / 500) loss: 1.160839
(Epoch 9 / 40) train acc: 0.713000; val_acc: 0.404000
(Epoch 10 / 40) train acc: 0.756000; val_acc: 0.418000
(Epoch 11 / 40) train acc: 0.791000; val_acc: 0.428000
(Epoch 12 / 40) train acc: 0.806000; val_acc: 0.394000
(Iteration 301 / 500) loss: 0.993981
(Epoch 13 / 40) train acc: 0.850000; val_acc: 0.400000
(Epoch 14 / 40) train acc: 0.848000; val_acc: 0.414000
(Epoch 15 / 40) train acc: 0.851000; val_acc: 0.432000
(Epoch 16 / 40) train acc: 0.879000; val_acc: 0.416000
(Iteration 401 / 500) loss: 0.901076
(Epoch 17 / 40) train acc: 0.893000; val_acc: 0.420000
(Epoch 18 / 40) train acc: 0.914000; val_acc: 0.412000
(Epoch 19 / 40) train acc: 0.933000; val_acc: 0.436000
(Epoch 20 / 40) train acc: 0.906000; val_acc: 0.414000
libpng warning: iCCP: cHRM chunk does not match sRGB
Validation set accuracy:  0.436
Test set accuracy:  0.386

结果