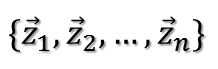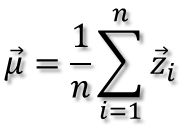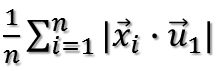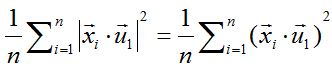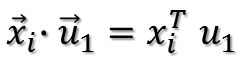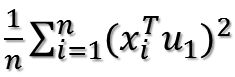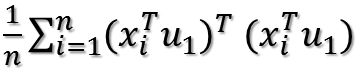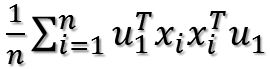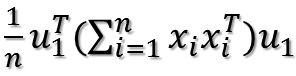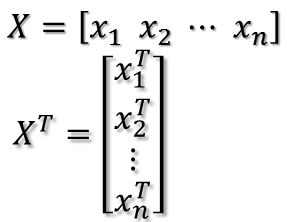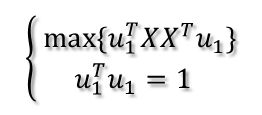写在前面的话:这部分基本上就是学习笔记,主要参考里面的博客已经写得很好,只是按自己的复习学习思路整理了下。
一、数学基础
1. 特征值和特征向量
特征值是线性代数中的一个重要概念。设 A 是n阶方阵,如果存在数m和非零n维列向量使得下式成立:
则称 是A的一个特征值。非零n维列向量 称为矩阵A对应于特征值 的特征向量,简称A的特征向量。
几何意义:通常来说,左乘一个矩阵会使得 在方向和长度上发生变化,但对于特征向量来说,却可以保持方向不变,只进行比例为 的伸缩。
2. SVD奇异值分解
由于特征值和特征向量只对方阵才有意义,所以针对不是方阵的情况提出了SVD。
假设给定了某一个矩阵A,其维度是m×n。那么,定义SVD为如下式:
其中,U是一个m×m的矩阵,Σ是一个m×n的矩阵,V是一个n×n的矩阵。Σ中,除了对角线上的元素之外,其余元素的值都为0,主对角线上的每个元素都被称为奇异值。另外,U和V都是经过标准化之后的,即满足:
推导过程可以参考:奇异值分解(SVD)原理详解及推导
3. 协方差矩阵
二、PCA推导
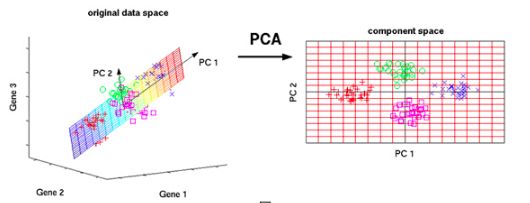
PCA的主要作用是降维,找出数据里最主要的方面,用数据里最主要的方面来代替原始数据:
例如,我们的数据集是n维的,共有m个数据(x(1),x(2),...,x(m))。我们希望将这m个数据的维度从n维降到k维,希望这m个k维的数据集尽可能的代表原始数据集。我们知道数据从n维降到k维肯定会有损失,但是我们希望损失尽可能的小。那么如何让这k维的数据尽可能表示原来的数据呢?
在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。借用信号的观点,最好的k维特征是将n维样本点转换为k维后,每一维上的样本方差都很大。
具体推导过程:
给定一组数据:(如无说明,以下推导中出现的向量都是默认是列向量)
将其中心化后表示如下,即得到了样本偏离的程度:
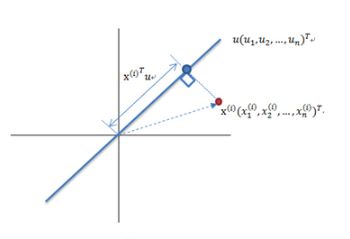
计算投影的方法就是将x与u1做内积,由于只需要求u1的方向,所以设u1是单位向量:
也就是最大化下式:
由矩阵代数相关知识可知,可以对绝对值符号项进行平方处理,比较方便。所以进而就是最大化下式:
两个向量做内积,可以转化成矩阵乘法:
所以目标函数可以表示为:
括号里面就是矩阵乘法表示内积,转置以后的行向量乘以列向量得到一个数。因为一个数的转置还是其本身,所以又可以将目标函数化为:
这样就可以把括号去掉,去掉以后变成:
由于u1和i无关,可以把它拿到求和符外面:
注意,其实括号里面是一个矩阵乘以自身的转置,这个矩阵形式如下:
其实将这个矩阵表示出来的话就会发现其实就是协方差矩阵,我们在优化降维后方差最大化的过程中折腾出协方差矩阵非常合理,也有从协方差矩阵角度出发讲解PCA的,比较好懂:PCA的数学原理
所以目标函数最后化为:
上式到底有没有最大值呢?如果没有前面的1/n,那就是就是一个标准的二次型,并且得到的矩阵是一个半正定的对称阵。为什么?首先是对称阵,因为=,下面证明它是半正定,什么是半正定?就是所有特征值大于等于0:
证明半正定阵的二次型的目标函数存在最大值:
对于向量x,其二范数(也就是模长)的平方为:
所以有:
使用矩阵范数不等式可以得到:
表示矩阵A的最大奇异值
既然证明了有最大值,后面就简单了,使用拉格朗日乘数法即可求出:
目标函数和约束条件构成了一个最大化问题:
构造拉格朗日函数:
对u1求导:
显然,u1即为特征值 对应的特征向量,则的所有特征值和特征向量都满足上式,那么将上式代入目标函数表达式即可得到:
所以,如果取最大的那个特征值,那么得到的目标值就最大。有可能你会有疑问,为什么一阶导数为0就是极大值呢?那么再求二阶导数:
二阶导数半负定,所以,目标函数在最大特征值所对应的特征向量上取得最大值。所以,第一主轴方向即为第一大特征值对应的特征向量方向。第二主轴方向为第二大特征值对应的特征向量方向,以此类推,证明类似。
三、PCA算法流程
求样本x(i)的k维的主成分其实就是求样本集的协方差矩阵 的前k个特征值对应特征向量矩阵W,然后对于每个样本x(i),做如下变换 ,即达到降维的PCA目的。
输入:n维样本集D=(x(1),x(2),...,x(m)),要降维到的维数k
输出:降维后的样本集
对所有的样本进行中心化:
计算样本的协方差矩阵
对矩阵 进行特征值分解
取出最大的k个特征值对应的特征向量(w1,w2,...,wn′), 将所有的特征向量标准化后,组成特征向量矩阵W
对样本集中的每一个样本x(i),转化为新的样本
得到输出样本集D′=(z(1),z(2),...,z(m))
现在主流的做法其实是使用SVD(奇异值分解)来求出主成分,因为当样本数和样本特征数都较多的时候,计算协方差矩阵的计算量会很大。SVD在不求解协方差矩阵的情况下,得到右奇异矩阵V。也就是说PCA算法可以不用做特征分解,而是做SVD来完成,这个方法在样本量很大的时候很有效。具体的求法可以参考:SVD与PCA之间的关系详解
四、机器学习实战中的代码
#coding= utf-8
import numpy as np
def loadDataSet(fileName, delim='\t'):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
datArr = [map(float,line) for line in stringArr]
return datArr
#利用协方差最大的方向进行降维
#:数据集;降维后的维度
#r :利用降维后的矩阵反构出原数据矩阵;降维后的数据
def pca(dataMat,topNfeat=9999999):
dataMat = np.mat(dataMat)
meanVals = np.mean(dataMat,axis=0)
meanRemoved = dataMat - meanVals
covMat = np.cov(meanRemoved,rowvar=0) #得到协方差矩阵
eigVals,eigVects = np.linalg.eig(np.mat(covMat)) #得到基于协方差矩阵的特征值和特征向量(一列表示一个特征向量)
eigValInd = np.argsort(eigVals) #对特征值进行排序(从小到大),返回其对应的数组索引(按从小到大顺序)
eigValInd = eigValInd[:-(topNfeat + 1):-1] #从排序后的矩阵最后一个开始自下而上选取最大的N个特征值,返回其对应的数组索引
redEigVects = eigVects[:,eigValInd] #从特征向量数组中取出特征值较大的特征向量组成数组
lowDDataMat = meanRemoved * redEigVects #将去除均值后的数据矩阵*压缩矩阵,转换到新的空间,使维度降低为N
# 利用降维后的矩阵反构出原数据矩阵(用作测试,可跟未压缩的原矩阵比对)
reconMat = (lowDDataMat * redEigVects.T) + meanVals
# 返回压缩后的数据矩阵即该矩阵反构出原始数据矩阵
return lowDDataMat,reconMat
import matplotlib
import matplotlib.pyplot as plt
def Pcaplot(dataMat,reconMat):
dataMat = np.mat(dataMat)
fig=plt.figure()
ax=fig.add_subplot(111)
#三角形表示原始数据点
ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90)
#圆形点表示第一主成分点,点颜色为红色
ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0], marker='o',s=90,c='red')
plt.show()
五、sklearn实现
class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)
Parameters:
n_components : 其取不同类型时的意义不一样,
默认为n_components=min(样本数,特征数)
int 类型:直接指定降维到的维度数目
float 类型:主成分的方差和所占的最小比例阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数
str 类型:参数设置为'mle'(极大似然估计), 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维copy : bool类型,默认值为True
表示是否在运行算法时,将原始数据复制一份。默认为True,则运行PCA算法后,原始数据的值不会有任何改变。whiten : bool类型,默认值为False
白化,就是对降维后的数据的每个特征进行标准化,让方差都为1。对于PCA降维本身来说,一般不需要白化。如果你PCA降维后有后续的数据处理动作,可以考虑白化svd_solver : string类型,默认值为'auto'
'auto': PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维
'full' :则是传统意义上的SVD,使用了scipy库对应的实现
'randomized' 一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法
'arpack' :和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。当svd_solve设置为'arpack'时,保留的成分必须少于特征数,即不能保留所有成分
tol : float类型,默认值为0
当svd_solver选择‘arpack’时,其运行SVD算法的容错率iterated_power : int类型或者str类型,默认值为‘auto’
当svd_solver选择‘randomized’时,其运行SVD算法的的迭代次数random_state: int类型,默认为None
伪随机数发生器的种子,在混洗数据时用于概率估计
Attributes:
- components_: 主成分
- explained_variance_:降维后的各主成分的方差值
- explained_variance_ratio_:降维后的各主成分的方差值占总方差值的比例
- singular_values_:对应的每个成分的奇异值
- mean_: X.mean(axis = 1)
- n_components_:主成分的个数
- noise_variance_:可参考: met-mppca
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
pca.fit(X)
>> PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
X_pca = pca.transform(x)
参考:
- https://blog.csdn.net/zhongkejingwang/article/details/42264479
- https://blog.csdn.net/zhongkelee/article/details/44064401
- http://www.cnblogs.com/pinard/p/6239403.html
- https://blog.csdn.net/hongbin_xu/article/list/2
- https://blog.csdn.net/baimafujinji/article/details/79407488