回归分析
从许多方面来看,回归分析都是统计学的核心。通常指用一个或者多个预测变量(自变量或解释变量)来预测响应变量(因变量,校标变量或结果变量)的方法。其中回归分析包括各种变种:
-
简单线性回归:用一个自变量预测一个因变量; -
多项式回归:用一个自变量预测一个因变量,模型的关系是n阶多项式; -
多元线性回归:用两个以上的自变量预测一个因变量; -
多变量回归:用多个自变量预测多个因变量; -
Logistic回归:用一个或多个自变量预测一个类别型因变量; -
泊松回归:用一个或多个自变量预测一个代表频数的因变量; -
Cox风险比例回归:用一个或多个自变量预测一个事件(死亡,失败或旧病复发)发生的时间 -
时间序列:对误差项相关的时间序列数据建模; -
非线性:用一个或多个自变量预测一个因变量,不过模型是非线性的; -
非参数:用一个或多个自变量预测一个因变量,模型的形式源自数据形式,不事先设定; -
稳健回归:用一个或多个自变量预测一个因变量,可以抵抗强影响点的干扰。
它其实是一个广义的概念,通指那些用一个或多个预测变量(也称自变量或解释变量)来预测响应变量(也称因变量、效标变量或结果变量)的方法。通常,回归分析可以用来挑选与响应变量相关的解释变量,可以描述两者的关系,也可以生成一个等式,通过解释变量来预测响应变量。我们需要注意等式的形式:
~左边为响应变量,右边为自变量;
+分隔预测变量;
:表示预测变量的交互项;
*表示所有可能交互项的简洁形式;
^表示交互项达到某个次数;
.表示除因变量外的所有自变量;
-表示从等式中移除某个变量;
-1表示删除截距项,使模型强制通过原点;
I()从算数的角度解释括号中的元素;
function表示可以在表达式中用的数学函数。
对于线性模型拟合过程中我们常常使用以下函数评价模型:
summary()展示模型拟合的详细结果;
coefficents()列出模型的参数
confint()提供模型的置信区间
fitted()列出模型的预测值
residuals()列出模型的残差
anova()生成模型的方差分析表,或者比较两个或更多模型的方差分析表
vcov()列出模型参数的协方差矩阵
AIC()输出赤池信息准则
plot()生成评价拟合模型的诊断图
predict()对新数据进行预测
简单线性回归
> fit <- lm(weight~height, data=women)
> summary(fit)
Call:
lm(formula = weight ~ height, data = women)
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -87.51667 5.93694 -14.74 1.71e-09 ***
height 3.45000 0.09114 37.85 1.09e-14 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
调用summary泛型函数可以获得以下信息,call列出回归模型的公式,Residuals列出了残差的分布,Coefficients表示系数项及其P值(估计系数为零假设的概率),Residual standard error表示残差标准误差(越小越好),Multiple R-squared衡量模型拟合质量的指标,表示回归模型所能解释的因变量的方差比例,F-statisticF统计量表明模型是否显著。
> coefficients(fit)
(Intercept) height
-87.51667 3.45000
> residuals(fit)
1 2 3 4 5 6 7 8
2.41666667 0.96666667 0.51666667 0.06666667 -0.38333333 -0.83333333 -1.28333333 -1.73333333
9 10 11 12 13 14 15
-1.18333333 -1.63333333 -1.08333333 -0.53333333 0.01666667 1.56666667 3.11666667
> fitted(fit)
1 2 3 4 5 6 7 8 9 10
112.5833 116.0333 119.4833 122.9333 126.3833 129.8333 133.2833 136.7333 140.1833 143.6333
11 12 13 14 15
147.0833 150.5333 153.9833 157.4333 160.8833
> confint(fit)
2.5 % 97.5 %
(Intercept) -100.342655 -74.690679
height 3.253112 3.646888
多项式回归
> fit2 <- lm(weight~height + I(height^2), data=women) # 多项式可以更好的拟合模型
> summary(fit2)
Call:
lm(formula = weight ~ height + I(height^2), data = women)
Residuals:
Min 1Q Median 3Q Max
-0.50941 -0.29611 -0.00941 0.28615 0.59706
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 261.87818 25.19677 10.393 2.36e-07 ***
height -7.34832 0.77769 -9.449 6.58e-07 ***
I(height^2) 0.08306 0.00598 13.891 9.32e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3841 on 12 degrees of freedom
Multiple R-squared: 0.9995, Adjusted R-squared: 0.9994
F-statistic: 1.139e+04 on 2 and 12 DF, p-value: < 2.2e-16
# 次数越高模型拟合效果越好,但是需要防止过拟合
> fit3 <- lm(weight~height + I(height^2) + I(height^3), data=women)
> summary(fit3)
Call:
lm(formula = weight ~ height + I(height^2) + I(height^3), data = women)
Residuals:
Min 1Q Median 3Q Max
-0.40677 -0.17391 0.03091 0.12051 0.42191
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.967e+02 2.946e+02 -3.044 0.01116 *
height 4.641e+01 1.366e+01 3.399 0.00594 **
I(height^2) -7.462e-01 2.105e-01 -3.544 0.00460 **
I(height^3) 4.253e-03 1.079e-03 3.940 0.00231 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2583 on 11 degrees of freedom
Multiple R-squared: 0.9998, Adjusted R-squared: 0.9997
F-statistic: 1.679e+04 on 3 and 11 DF, p-value: < 2.2e-16
多元线性回归
> fit <- lm(mpg~hp+wt+hp:wt, data=mtcars)
> summary(fit)
Call:
lm(formula = mpg ~ hp + wt + hp:wt, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.0632 -1.6491 -0.7362 1.4211 4.5513
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.80842 3.60516 13.816 5.01e-14 ***
hp -0.12010 0.02470 -4.863 4.04e-05 ***
wt -8.21662 1.26971 -6.471 5.20e-07 ***
hp:wt 0.02785 0.00742 3.753 0.000811 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.153 on 28 degrees of freedom
Multiple R-squared: 0.8848, Adjusted R-squared: 0.8724
F-statistic: 71.66 on 3 and 28 DF, p-value: 2.981e-13
多元回归需要考虑自变量之间的交互项,交互项表示因变量与其中一个自变量的关系依赖于另一个自变量的水平,在这里交互项表示每加仑汽油行驶的里程数与汽车马力的关系根据车重的不同而不同。当我们存在多个自变量时,自变量之间会存在多种模式,如何从众多可能的模型中筛选最佳模型呢,这时候就需要一些统计量比较模型,例如AIC,BIC等,其考虑了模型统计拟合度以及用于拟合的参数数量,值越小表示模型越好,可以使用step()或者MASS包中的stepAIC()进行逐步回归筛选模型。
回归诊断
我们使用lm()函数来拟合OLS回归模型,通过summary()函数获取模型参数和相关统计量。但是,没有任何输出告诉你模型是否合适,你对模型参数推断的信心依赖于它在多大程度上满足OLS模型统计假设。为什么这很重要?因为数据的无规律性或者错误设定了预测变量与响应变量的关系,都将致使你的模型产生巨大的偏差。一方面,你可能得出某个预测变量与响应变量无关的结论,但事实上它们是相关的;另一方面,情况可能恰好相反。当你的模型应用到真实世界中时,预测效果可能很差,误差显著。
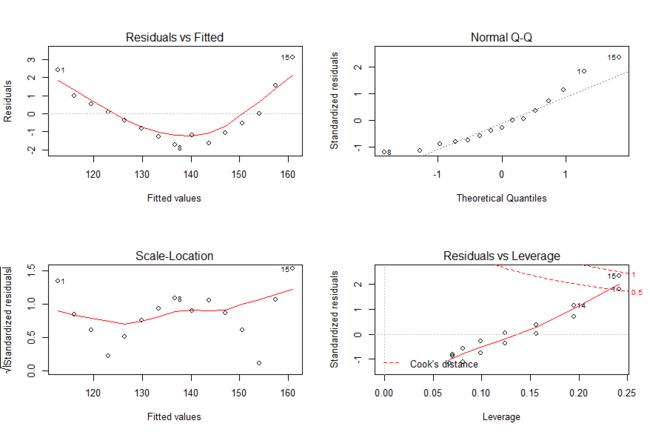
我们可以通过plot()函数,可以生成评价模型拟合情况的四幅图形,帮助我们判断样本是否符合正态分布假设?是否存在离群值导致模型产生较大误差?线性模型是否合理?残差是否满足独立性、等方差、正态分布等假设条件?以及是否存在多重共线性?
> fit <- lm(weight ~ height, data=women)
> par(mfrow=c(2,2))
> plot(fit)
OLS回归的统计假设应满足正态性,独立性,线性,同方差性。
- 若因变量与自变量线性相关,那么残差值与预测(拟合)值就没有任何系统关联。换句话说,除了白噪声,模型应该包含数据中所有的系统方差。在“残差图与拟合图”(Residuals vs Fitted,左上)中可以清楚地看到一个曲线关系,这暗示着你可能需要对回归模型加上一个二次项。
- 当预测变量值固定时,因变量成正态分布,则残差值也应该是一个均值为0的正态分布。“正态Q-Q图”(Normal Q-Q,右上)是在正态分布对应的值下,标准化残差的概率图。若满足正态假设,那么图上的点应该落在呈45度角的直线上;若不是如此,那么就违反了正态性的假设。
- 若满足不变方差假设,那么在“位置尺度图”(Scale-Location Graph,左下)中,水平线周围的点应该随机分布。该图似乎满足此假设。或者使用
car包中的ncvTest()判断误差方差是否恒定
> ncvTest(fit)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.8052115, Df = 1, p = 0.36954
记分检验不显著:p=0.36954,说明满足方差不变假设
- 最后一幅“残差与杠杆图”(Residuals vs Leverage,右下)提供了可能关注的单个观测点的信息。从图形可以鉴别出离群点、高杠杆值点和强影响点。强影响点(influential observation)对模型参数的估计产生的影响过大,非常不成比例。强影响点可以通过Cook距离即Cook’s D统计量来鉴别
- 对于独立性检验
car包提供了durbinWatsonTest()函数,用于做Durbin-Watson检验,检测误差的序列相关性。
> durbinWatsonTest(fit)
lag Autocorrelation D-W Statistic p-value
1 0.585079 0.3153804 0
Alternative hypothesis: rho != 0
p值<0.05,不显著,误差项之间独立,不存在自相关性。
- 多重共线性可用统计量VIF(Variance Inflation Factor,方差膨胀因子)进行检测。VIF的平方根表示变量回归参数的置信区间能膨胀为与模型无关的预测变量的程度(因此而得名)。
car包中的vif()函数提供VIF值。一般原则下, vif >2就表明存在多重共线性问题。可以通过构建具有正则化项的岭回归来解决多重共线性问题。
综合检测:gvlma包中的gvlma()能对线性模型假设进行综合验证,同时还能做偏斜度、峰度和异方差性的评价
> gvmodel <- gvlma(fit3)
> summary(gvmodel)
Call:
lm(formula = weight ~ height + I(height^2) + I(height^3), data = women)
Residuals:
Min 1Q Median 3Q Max
-0.40677 -0.17391 0.03091 0.12051 0.42191
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.967e+02 2.946e+02 -3.044 0.01116 *
height 4.641e+01 1.366e+01 3.399 0.00594 **
I(height^2) -7.462e-01 2.105e-01 -3.544 0.00460 **
I(height^3) 4.253e-03 1.079e-03 3.940 0.00231 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2583 on 11 degrees of freedom
Multiple R-squared: 0.9998, Adjusted R-squared: 0.9997
F-statistic: 1.679e+04 on 3 and 11 DF, p-value: < 2.2e-16
ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS
USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM:
Level of Significance = 0.05
Call:
gvlma(x = fit3)
Value p-value Decision
Global Stat 5.679241 0.22442 Assumptions acceptable.
Skewness 0.006034 0.93808 Assumptions acceptable.
Kurtosis 0.120598 0.72839 Assumptions acceptable.
Link Function 4.426151 0.03539 Assumptions NOT satisfied!
Heteroscedasticity 1.126457 0.28853 Assumptions acceptable.