树
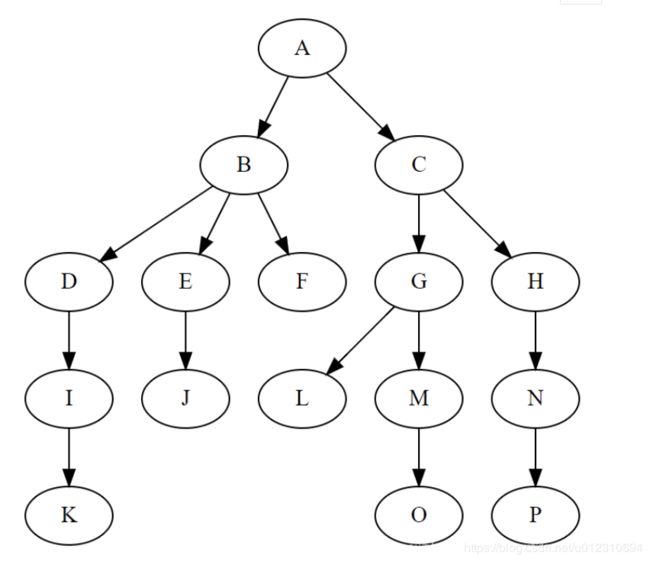
在计算机科学中,树(英语:tree)是一种抽象数据类型或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
①每个节点有零个或多个子节点;
②没有父节点的节点称为根节点;
③每一个非根节点有且只有一个父节点;
④除了根节点外,每个子节点可以分为多个不相交的子树;
关于树的术语
根节点:没有父节点的节点;
叶子节点:树的末端,不含子节点的节点;
高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0。上图中,根节点A的深度为0,D节点的深度为2;
二叉树
每个节点最多含有两个子节点的树称为二叉树(大多数情况下我们遇到的树都是二叉树,但是不代表所有的树都是二叉树)
二叉树的遍历
前序遍历:根结点 ---> 左子树 ---> 右子树
中序遍历:左子树---> 根结点 ---> 右子树
后序遍历:左子树 ---> 右子树 ---> 根结点
层次遍历:从顶部到底部,从左边到右边
(前中后其实是针对于根节点的顺序)
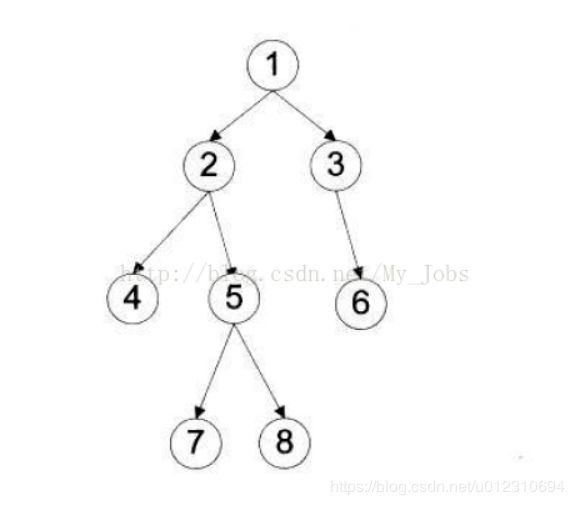
前序遍历:1 2 4 5 7 8 3 6
中序遍历:4 2 7 5 8 1 3 6
后序遍历:4 7 8 5 2 6 3 1
层次遍历:1 2 3 4 5 6 7 8
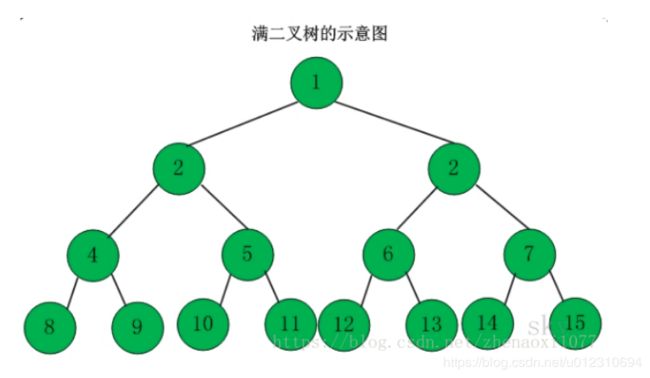
满二叉树
一棵有n层的二叉树,除第n层外,每层都有两个子节点,那么这棵树就是满二叉树。
换一种说法,除叶子节点外,每个节点都有两个子节点。节点数达到最大值,所有叶子节点均在同一层。
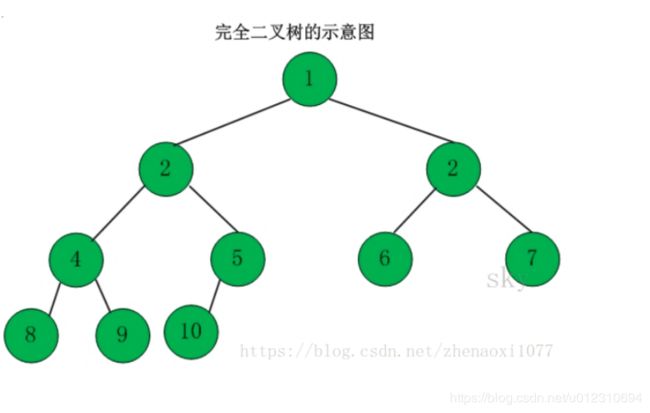
完全二叉树
完全二叉树由满二叉树引进而来。假设二叉树有h层,除第h层外,其他各层的节点数均已达到最大个数(1至h-1层为满二叉树),第h层所有的节点都集中在最左边,这棵树就是完全二叉树。
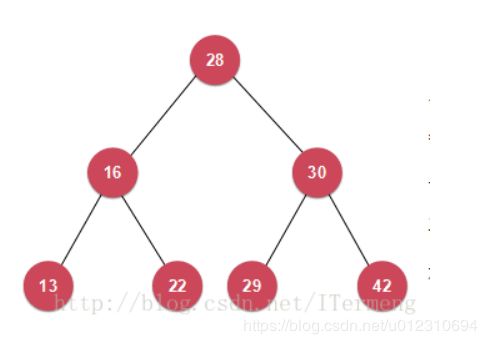
二叉查找树
又称为二叉搜索树、有序二叉树、排序二叉树
特性:
1.若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2. 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3.任意节点的左、右子树也分别为二叉查找树;
4.没有键值相等的节点。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低为 O ( log n ) 。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。
平衡二叉树(AVL树)
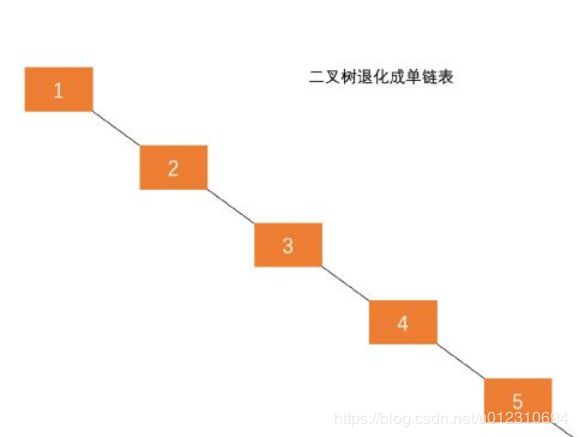
尽管二叉查找树有较高的查询性能,但是在某些情况下,二叉查找树会退化成条链表,时间复杂度为O(n),效率降低,这时候我们需要用到平衡二叉树。
平衡二叉树特点:
1.平衡二叉树要么是一棵空树;
2.要么保证左右子树的高度之差不大于 1;
3.子树也必须是一颗平衡二叉树;
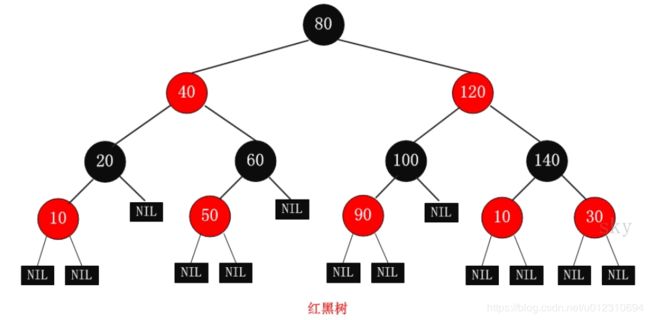
红黑树
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。
特点:
1.每个节点或者是黑色,或者是红色。
2.根节点是黑色。
3.每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
4.如果一个节点是红色的,则它的子节点必须是黑色的。
5.从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
赫夫曼树(最优二叉树)
大家可能更多听说的是哈夫曼编码,其实就是哈夫曼树的应用。
待续
B树
B树,Balance Tree,即为平
衡树
一个m阶的B树具有如下几个特征:
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
B 树中如何查找数据
B 树的子树大小排序规则,因此在 B 树中查找数据时,一般需要这样:
1.从根节点开始,如果查找的数据比根节点小,就去左子树找,否则去右子树
2.和子树的多个关键字进行比较,找到它所处的范围,然后去范围对应的子树中继续查找
3.以此循环,直到找到或者到叶子节点还没找到为止
B 树的每个节点可以表示的信息更多,因此整个树更加“矮胖”,这在从磁盘中查找数据(先读取到内存、后查找)的过程中,可以减少磁盘 IO 的次数,从而提升查找速度。
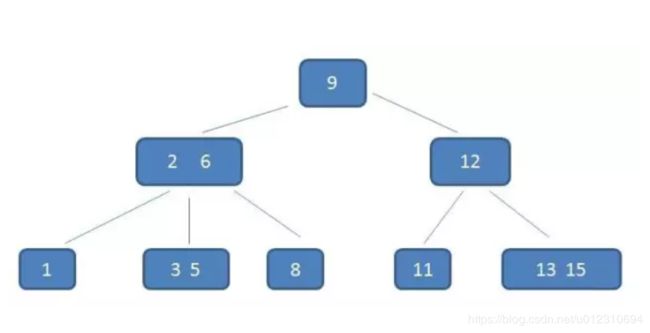
B+树
B+ 树是对 B 树的进一步优化。
B+ 树和 B 树不同之处:
1.B+ 树非叶子节点上是不存储数据的,仅存储键值,而 B 树节点中不仅存储键值,也会存储数据。
2.因为 B+ 树索引的所有数据均存储在叶子节点,而且数据是按照顺序排列的。
B+是在在B树基础上,为叶子结点增加链表指针(B树+叶子有序链表),所有关键字都在叶子结点 中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中。
参考资料:
树:https://blog.csdn.net/wannuoge4766/article/details/83998377
平衡二叉树:https://zhuanlan.zhihu.com/p/56066942
维基百科中关于树的解释:https://zh.wikipedia.org/wiki/%E6%A0%91_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84)
红黑树:https://www.cnblogs.com/skywang12345/p/3245399.html
B树:https://database.51cto.com/art/201911/605881.htm
参考书籍:
《数据结构与算法分析》
《数据结构(C语言版)/清华大学计算机系列教材》