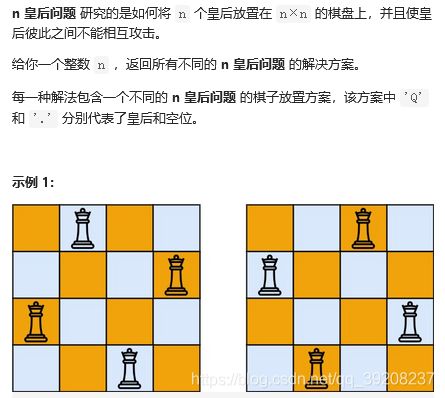
N皇后问题
N皇后是一道应用回溯算法的经典例题。
N皇后研究的是如何将 N 个皇后放置在 N×N 的棋盘上,并且使皇后彼此之间不能相互攻击
而两个皇后可以相互攻击的条件是:
二者必须位于棋盘的同一行,或者同一列,或者同一斜线上
N皇后
比如现在研究4皇后问题,棋盘如下:

我们要把4个皇后放入棋盘,使它们不能两两攻击!

根据皇后互相攻击要满足的条件,我们很容易获得阻止皇后互相攻击的手段(怎么能容忍可爱的猫猫打架呢?):
使任何两个皇后都不处于同一条横行、纵行或斜线上即可
现在假设棋盘上已经放了3个皇后,要放最后一个皇后,我们需要放在最后一行的哪个格子里呢?

当然是第2个格子了!

但编写算法时,算法可没长眼睛,它并不能一下子看出来应该放在第二个格子。我们需要一个辅助函数,去判断最后一行的哪个格子可以放置皇后,能保证皇后不攻击。
那现在我们要设计这个辅助函数,给算法充当眼睛。当然,该辅助函数需要知道棋盘的现状及要检测的位置。
有了这些输入参数后,判断可不可以放置就很简单了,只要排除互相攻击的条件即可。保证皇后不攻击我们只需要检测打算放置皇后的位置的商下左右及4条斜线,共计8个方向有没有皇后即可。

上图这个位置因为位于边角,所以有5个方向越界,但若是要放置的位置并不是边角,那么8个方向是妥妥的,边角位置我们用循环控制一下就好。
但实际上我们只需要检测3个方向即可,因为我们在每一行仅仅放置一个皇后,那么目标行根本不用检测,还不存在皇后,一下少2个方向(左,右)。目标行之下的3个方向(正下,左斜下,右斜下)也不用检测,因为目标行都没有皇后,它下面更不可能存在皇后了。
所以在辅助函数里只要检测8-2-3=3个方向即可,辅助函数很容易写出来:
bool IsValid(const vector<string>& tmp,const int& row,const int& col,const int& n);
//vector tmp:棋盘,每一行是一个字符串,有皇后的位置用Q表示,否则.表示
//row:检测目标行 col:目标检测列 n:棋盘边长
//布尔型返回值,true代表位置(row,col)可以放置皇后Q,false表示不可
//因为是辅助函数,我们只希望该函数告诉我们(row,col)位置能不能放置皇后Q即可,不允许辅助函数对棋盘或者传入参数做任何修改!因此一律加const修饰
//不修改参数的函数,我们用引用传参可以提高效率,因为传引用不会开辟空间存储参数
那么辅助函数实现就如下了:
bool IsValid(const vector<string>& tmp,const int& row,const int& col,const int& n){
for(int i = row - 1;i>=0;--i){
//正上方
if(tmp[i][col] == 'Q')
return false;
}
for(int i = row - 1,j = col + 1;i>=0&&j<n;--i,++j){
//右斜上
if(tmp[i][j]=='Q')
return false;
}
for(int i = row - 1,j = col - 1;i>=0&&j>=0;--i,--j){
//左斜上
if(tmp[i][j]=='Q')
return false;
}
return true;
}
正题开始!
那现在我们如何从0开始?万事开头难,第一个皇后怎么放置?
那么,回溯来了!
其实回溯就是一种暴力算法,它会穷举所有支路,然后去试探哪条支路满足条件,满足则继续沿着这条支路继续向下找,反之则会放弃该支路,继续去找其他满足条件的支路。
第一个皇后放在第一行任意位置都可以(用IsValid()判断):
 我们就列举第一个皇后放在第一行第三列的支路示意一下,被大红×划掉的支路都是
我们就列举第一个皇后放在第一行第三列的支路示意一下,被大红×划掉的支路都是IsValid()返回false的支路,继续向下找的都是返回true的支路:
 【NOTE】:上图有错误!应该是最后一层的第二个方案正确!而不是第四个
【NOTE】:上图有错误!应该是最后一层的第二个方案正确!而不是第四个
很明显,在穷举支路时有两种情况:
1.该支路被否决,继续寻找其他支路
2.该支路满足条件,向下寻找
有没有很熟悉?递归是吧?简直一模一样好叭!
递归我相信很多人都能写出来,直接贴代码应该咩有问题
void BackTrack(vector<string>& tmp,int row,const int& n){
if(row == n){
//N个皇后已放置完毕
res.push_back(tmp);//支路结果存储
return;//结束
}
for(int col = 0;col<n;++col){
if(!IsValid(tmp,row,col,n))//不满足条件的支路
continue;
tmp[row][col] = 'Q';//满足条件的位置放入皇后
BackTrack(tmp,row+1,n);//继续向下寻找
tmp[row][col] = '.';//拿掉皇后
}
}
应该会有部分伙伴对拿掉皇后这一步有疑问,为什么要有这么一句?
请注意!棋盘自始至终只有一个
 我们在控制第一行格子的循环里给第三个格子放了皇后,然后找出了该支路的所有可能。算法回过头来想将皇后放置在第一行第四格,根本没办法放置皇后!一行只能放置一个啊。
我们在控制第一行格子的循环里给第三个格子放了皇后,然后找出了该支路的所有可能。算法回过头来想将皇后放置在第一行第四格,根本没办法放置皇后!一行只能放置一个啊。
所以这就是回溯算法的精髓之一:
民法边缘试探一脚(试探完了)->收回脚丫子->刑法边缘试探一脚(试探完了)->收回脚丫子->……->所有法律被试完了,死心了,睡觉.
那么N皇后到这基本讲完了。
完整CODE
class Solution {
public:
vector<vector<string>> res;
bool IsValid(const vector<string>& tmp,const int& row,const int& col,const int& n){
for(int i = row - 1;i>=0;--i){
//上方
if(tmp[i][col] == 'Q')
return false;
}
for(int i = row - 1,j = col + 1;i>=0&&j<n;--i,++j){
//右上方
if(tmp[i][j]=='Q')
return false;
}
for(int i = row - 1,j = col - 1;i>=0&&j>=0;--i,--j){
//左上方
if(tmp[i][j]=='Q')
return false;
}
return true;
}
void BackTrack(vector<string>& tmp,int row,const int& n){
if(row == n){
res.push_back(tmp);
return;
}
for(int col = 0;col<n;++col){
if(!IsValid(tmp,row,col,n))
continue;
tmp[row][col] = 'Q';
BackTrack(tmp,row+1,n);
tmp[row][col] = '.';
}
}
vector<vector<string>> solveNQueens(int n) {
vector<string> tmp(n,string(n,'.'));
BackTrack(tmp,0,n);
return res;
}
};
会了N皇后,当然要来挑战一下N皇后II了呀!
N皇后II
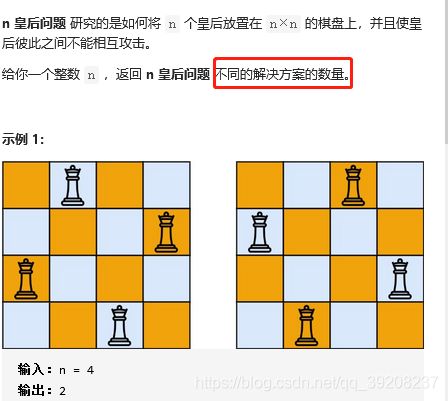 很明显,没有什么大的区别啊,仍然回溯就可以了。用N皇后的CODE照样可以解决N皇后II,只需要稍微改动一下就行了,如下:
很明显,没有什么大的区别啊,仍然回溯就可以了。用N皇后的CODE照样可以解决N皇后II,只需要稍微改动一下就行了,如下:
class Solution {
public:
vector<vector<string>> res;
bool IsValid(const vector<string>& tmp,const int& row,const int& col,const int& n){
for(int i = row - 1;i>=0;--i){
//上方
if(tmp[i][col] == 'Q')
return false;
}
for(int i = row - 1,j = col + 1;i>=0&&j<n;--i,++j){
//右上方
if(tmp[i][j]=='Q')
return false;
}
for(int i = row - 1,j = col - 1;i>=0&&j>=0;--i,--j){
//左上方
if(tmp[i][j]=='Q')
return false;
}
return true;
}
void BackTrack(vector<string>& tmp,int row,const int& n,int& count){
//多个count传入
if(row == n){
++count;//可能支路方案+1
return;
}
for(int col = 0;col<n;++col){
if(!IsValid(tmp,row,col,n))
continue;
tmp[row][col] = 'Q';
BackTrack(tmp,row+1,n,count);//注意count的传入
tmp[row][col] = '.';
}
}
int totalNQueens(int n) {
vector<string> tmp(n,string(n,'.'));
int count = 0;//记录方案数目
BackTrack(tmp,0,n,count);
return count;
}
};

看!稍微改几下就做完了!但这有什么意思呢?完全没得到提高,根本没有利用到红色方框里的信息啊!

人家只需要方案数量!方案数量 !方案数量!
我们完全不用去保存每个方案啊!上面那个稍微改动的代码可是把每种可能结果保存下来了!看看下面这个表:
| N | 方案结果数目 |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 2 |
| 5 | 10 |
| 6 | 4 |
| 7 | 40 |
| 8 | 92 |
| 9 | 352 |
| 10 | 724 |
| 11 | 2680 |
| 12 | 14200 |
| 13 | 73712 |
| 14 | 365596 |
| 15 | 2279184 |
| 16 | 14772512 |
| 17 | 95815104 |
| 18 | 666090624 |
| 19 | 4968057848 |
| 20 | 39029188884 |
| 21 | 314666222712 |
| 22 | 2691008701644 |
| 23 | 24233937684440 |
| 24 | 227514171973736 |
| 25 | 2207893435808352 |
好家伙!这恐怕是顶不住啊!这要是都保存结果,恐怕电脑撑不住啊
当然,这道题人家说了
1<=n<=9
没那么恐怖,我们还是秉持能优化就优化一下叭!
不需要方案,只需要方案数量,那么我们不需要保存方案。
原来我们可以看做是二维数组在保存结果,且每个正确的方案都保存了!
在和舍友日常交流中,意外谈到N皇后的结果用一维数组保存,因此有了下面的解法。
我们能不能用一维去充当一个临时空间,去保存一下可能的方案,所有的方案都用这一个一维数组去试?
看!二维数组降维成一维数组了!二维的行索引就是一维的索引,二维存在皇后的列数用所在列存储!即可完成空间复杂度的优化!
这个优化就是在IsValid()有较大改变,索引变成了行数,需要我们去仔细计算一下。有兴趣的伙伴可以自己算一下,也是对自己的一种提高鸭!
完整Code
class Solution {
public:
bool IsValid(const vector<int>& tmp,const int& row,const int& col){
for(int i = row - 1;i >= 0;--i){
//上方
if(tmp[i] == col)
return false;
if(tmp[i] == col - row + i)//左上方
return false;
if(tmp[i] == col + row - i)//右上方
return false;
}
return true;
}
void BackTrack(vector<int>& tmp,int row,int& cnt,const int& n){
if(row == n){
++cnt;
return;
}
for(int col = 0;col<n;++col){
if(!IsValid(tmp,row,col))
continue;
tmp[row] = col;
BackTrack(tmp,row+1,cnt,n);
}
}
int totalNQueens(int n) {
vector<int> tmp(n);
int cnt = 0;
BackTrack(tmp,0,cnt,n);
return cnt;
}
};
走心的伙伴可能会发现这个解答回溯里面竟然没有撤销的语句?!为什么没有?你可能需要好好想想,这个解法里我们需要撤销操作吗?或者说是不是撤销已经无形被执行了呢?想明白这一点,回溯可能能用的更灵活一点!
 这就是两道N皇后的题解了,当然,回溯可能说的还不是很清楚,目前我理解的回溯就是暴力+试探+撤销+递归这4个标签了,它适合那些需要遍历所有可能的题,时间复杂度较高,暂时也没有更深入的理解了,见谅。
这就是两道N皇后的题解了,当然,回溯可能说的还不是很清楚,目前我理解的回溯就是暴力+试探+撤销+递归这4个标签了,它适合那些需要遍历所有可能的题,时间复杂度较高,暂时也没有更深入的理解了,见谅。