论文《Attentive Collaborative Filtering: Multimedia Recommendation with Item- and Componet-Level ...》阅读
论文《Attentive Collaborative Filtering: Multimedia Recommendation with Item- and Component-Level Attention》阅读
- 论文概况
- Introduction
- Preliminaries
- Attentive Collaborative Filtering
- 总结
论文概况
这篇文章是新加坡国立大学何向南老师团队关于推荐系统方向的一篇论文,提出基于item和component层面的多媒体注意力模型ACF,被SIGIR 2017录用。文章主要聚焦在多媒体(视频/图像)推荐和注意力两方面。
本文的公式比较多,建议对照原文查看,这里只对文中的公式进行解析,建议对照原文查看,旨在节省各位同学的宝贵科研时间,方便同学快速了解ACF模型。
论文地址:ACF
代码地址未公开
Introduction
本文应用场景是多媒体推荐,作者给出了在图像和视频方面的推荐方案。
作者首先给出item和component的定义。item就是推荐场景中较常见的推荐物品;component在文中作者将其称为图像的某块区域或者视频中的某一帧。
针对图像来说,使用CV届比较知名的何凯明的ResNet-152模型res5c层的输出作为图像特征,将772048转为49*2048,也就是本文所说的component,共49个2048维不同区域构成了component。
针对视频,同样适用ResNet-152模型,将pool5层的输出作为每一帧的特征。这里作者针对4.3节中所说的“ x l ∗ x_{l*} xl∗ 代表每个不同item具有变长”也没有进一步说明,但是批处理必须有定长,需要padding或者截断,作者也没有说明他们具体是如何操作的。欢迎评论区大家参与讨论。
Preliminaries
这里作者介绍了BPR损失和平方差损失的区别,总结来说,针对implicit feedback场景,BPR表达能力更好一些,因为在数据集中标0的交互场景,不一定是user不喜欢这个item,也有可能是没看到。
Attentive Collaborative Filtering
首先,本文的总体架构图如下:
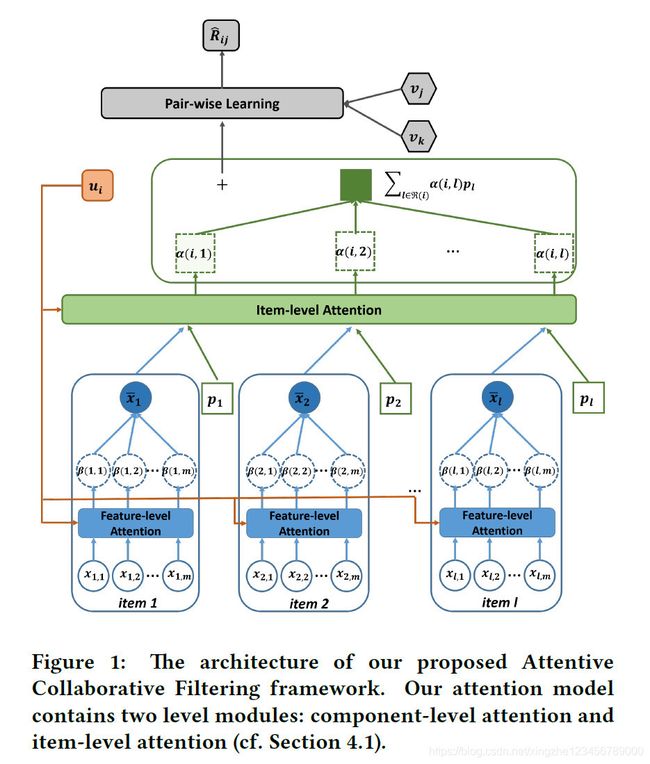
从这张图可以看到, u u u 、 v v v 、 p p p 分别表示用户、item、item的辅助向量,都是latent vector,属于learnable variables。向量 x ˉ \bar{x} xˉ 表示注意力组合之后的各个component的总体表示。
公式(5)表示user和item之间的interaction模拟,使用BPR损失的方式完成。公式中使用 u i + ∑ l ∈ R ( i ) α ( i , l ) p l u_i+\sum\limits_{l\in\mathcal{R}(i)}\alpha(i,\ l)p_l ui+l∈R(i)∑α(i, l)pl 表示用户本身的latent vector 加上注意力加权的辅助vector。
公式(5)只有 α ( i , l ) \alpha(i,\ l) α(i, l) 是还没有计算的,由公式(9)可知 α ( i , l ) \alpha(i,\ l) α(i, l) 是由 a ( i , l ) a(i,\ l) a(i, l) 通过softmax归一化后得到的。
a ( i , l ) a(i,\ l) a(i, l) 由公式(8)可知,是由 u i u_i ui 、 v l v_l vl 、 p l p_l pl、 x ˉ l \bar{x}_l xˉl 共同决定的。公式(8)是component-level注意力的计算方法。通过这个两层MLP层来计算,代表着用户 u 对 物体 i 针对所有 组件(component)的注意之和。 u i u_i ui 、 v l v_l vl 、 p l p_l pl都是初始化后需要模型优化的参数,公式(8)的计算又落到了 x ˉ l \bar{x}_l xˉl 的头上。
由公式(12)可知, x ˉ l \bar{x}_l xˉl 是component向量在component-level 注意力加权之和。
x l m x_{lm} xlm是由ResNet-152学习到的输入特征。其中, β ( i , l , m ) \beta(i,\ l,\ m) β(i, l, m) 代表用户i 对 物体l 的 组成部分 m 的注意力。这个注意力 β ( i , l , m ) \beta(i,\ l,\ m) β(i, l, m)是通过 b ( i , l , m ) b(i,\ l,\ m) b(i, l, m) 经过softmax归一化后得到的。而 b ( i , l , m ) b(i,\ l,\ m) b(i, l, m) ,由公式(10)可知,则是通过一个两层的MLP计算得到的,输入包括 u i u_i ui, x l m x_{lm} xlm,代表用户 u 对 组成部分 x l m x_{lm} xlm 的注意力大小。
总结
本文提出了基于item层和component层的Attention机制用于处理多媒体领域的推荐任务,提出了注意力协同过滤模型ACF。
本文总体架构图画得非常清晰,可以很清晰地了解整体架构。
一些个人观点:本文符号表示稍微有点混乱,和主流文章符号不太相同,经常对错号。同时文章对于component-level 和 item-level attention有一个empirical的介绍,但是具体为什么选用2层MLP进行计算没有进行解释。