K-近邻算法（k-NN）的原理及python代码案例实现

1 K-NN算法的原理

1.1 K-NN概念

       K Nearest Neighbor算法⼜叫KNN算法， 这个算法是机器学习⾥⾯⼀个⽐较经典的算法， 总体来说KNN算法是相对⽐
较容易理解的算法。

定义：
        如果⼀个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某⼀个类别， 则该样本也属于这

个类别。（起源：KNN最早是由Cover和Hart提出的一种分类算法）；俗话就是：根据“邻居”来推断出你的类别。

1.2 基本流程

1)计算已知类别数据集中的点与当前点之间的距离2)按距离递增次序排序
3)选取与当前点距离最小的k个点
4)统计前k个点所在的类别出现的频率
5)返回前k个点出现频率最高的类别作为当前点的预测分类

什么意思呢？看下这张图

根据上来面的流程来讲：

1.给定了红色和蓝色的训练样本，绿色为测试样本
2.计算绿色点到其他点的距离
3.选取离绿点最近的k个点
4.选取k个点中，同种颜色最多的类。例如：k=1时，k个点全是蓝色，那预测结果就是Class 1；k=3时，k个点中两个红色一个蓝色，那预测结果就是Class 2

举个实例：电影类型分析

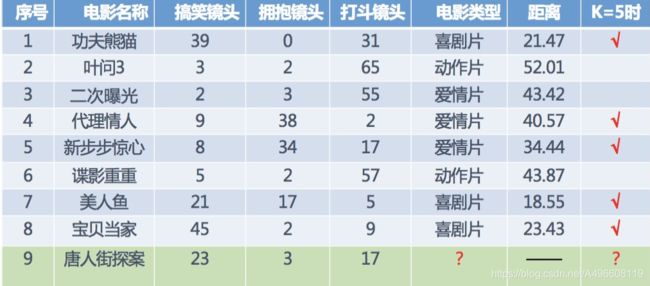
假设我们现在有几部电影，如下图所示：

其中9号电影属于什么电影类型的电影呢？如何去预测，我们可以利用k近邻算法的思想去算：

分别计算每个电影与9号电影之间的距离（这里采用欧氏距离算法），然后求解得到下图：

结果分析：由上图易知，当K= 3 时，三个都是喜剧片，根据判断法则，9号电影属于喜剧片；当K=5时，有三个喜剧片，有两个爱情片，根据判断法则，9号电影属于喜剧片；

1.3 K值的选择

k值过大：容易受到异常点的影响

K值过小：受到样本均衡的问题（如果不同种类的样本数量一样多，当 K=样本数/种类 时，就不能对未知数据进行分类判断）

K值选择问题，李航博士的一书「统计学习方法」上所说：

1) 选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

2) 选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

3) K=N（N为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组:训练集和验证集）来选择最优的K值。

• 近似误差：
  • 对现有训练集的训练误差，关注训练集，
  • 如果近似误差过小可能会出现过拟合的现象（过拟合：对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。）
  • 模型本身不是最接近最佳模型。
• 估计误差：
  • 可以理解为对测试集的测试误差，关注测试集，
  • 估计误差小说明对未知数据的预测能力好，
  • 模型本身最接近最佳模型。

小结：

• K值过小：
  • 容易受到异常点的影响
  • 容易过拟合
• k值过大：
  • 受到样本均衡的问题
  • 容易欠拟合

1.4距离公式内容的补充：（其它公式后期补上）

欧氏距离：

2 案例：鸢尾花种类预测 

 lris数据集是常用的分类实验数据集，由Fisher,1936收集整理。lris也称鸢尾花卉数据集，是一类多重变量分析的数据集。关于数据集的具体介绍:

2.1分析步骤

1.获取数据集
2.数据基本处理
3.特征⼯程
4.机器学习(模型训练)
5.模型评估

2.2代码实现

代码涉及sklean库，需要安装sklearn库，百度一下就知道怎么安装了。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

# 1.获取数据
iris = load_iris()

# 2.数据基本处理：训练集的特征值x_train 测试集的特征值x_test 训练集的⽬标值y_train 测试集的⽬标值y_test，
'''
x: 数据集的特征值
y: 数据集的标签值
test_size: 测试集的⼤⼩， ⼀般为float
random_state: 随机数种⼦,不同的种⼦会造成不同的随机采样结果。 相同的种⼦采样结果相同
'''
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)

# 3.特征工程 - 特征预处理
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习-KNN
# 4.1 实例化一个估计器
estimator = KNeighborsClassifier(n_neighbors=5)
# 4.2 模型训练
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 预测值结果输出
y_pre = estimator.predict(x_test)
print("预测值是:\n", y_pre)
print("预测值和真实值的对比是:\n", y_pre==y_test)

# 5.2 准确率计算
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)

实验结果：最终结果达到了0.9333

3 k近邻算法优缺点汇总

优点：
1.简单有效
2.重新训练的代价低
3.适合类域交叉样本
        KNN⽅法主要靠周围有限的邻近的样本,⽽不是靠判别类域的⽅法来确定所属类别的， 因此对于类域的交叉或重叠较多的待分样本集来说， KNN⽅法较其他⽅法更为适合。
4.适合⼤样本⾃动分类
       该算法⽐较适⽤于样本容量⽐较⼤的类域的⾃动分类， ⽽那些样本容量较⼩的类域采⽤这种算法⽐较容易产⽣误分。
缺点：
1.惰性学习
KNN算法是懒散学习⽅法（lazy learning,基本上不学习） ， ⼀些积极学习的算法要快很多
2.类别评分不是规格化
不像⼀些通过概率评分的分类
3.输出可解释性不强
例如决策树的输出可解释性就较强
4.对不均衡的样本不擅⻓
当样本不平衡时， 如⼀个类的样本容量很⼤， ⽽其他类样本容量很⼩时， 有可能导致当输⼊⼀个新样本时， 该样本的K个邻居中⼤容量类的样本占多数。 该算法只计算“最近的”邻居样本， 某⼀类的样本数量很⼤， 那么或者这类样本并不接近⽬ 标样本， 或者这类样本很靠近⽬ 标样本。 ⽆论怎样， 数量并不能影响运⾏结果。 可以采⽤权值的⽅法（和该样本距离⼩的邻居权值⼤） 来改进。

参考：1.https://www.cnblogs.com/ishero/p/11136304.html 2.黑马机器学习算法课程