胶囊神经网络详解

目录

背景介绍

卷积神经网络不足之处

位姿

胶囊是什么？

胶囊的工作原理

1.输入向量的矩阵乘法

2.输入向量的标量加权

3.加权输入向量之和

4. 向量到向量的非线性变换

囊间动态路由算法(精髓所在）

损失函数

编码器

解码器

性能评估

---

 

---

背景介绍

Geoffrey Hinton，深度学习的开创者之一，反向传播等神经网络经典算法的发明人，2017年10月发表了论文，介绍了全新的胶囊网络模型，以及相应的囊间动态路由算法。

论文https://arxiv.org/pdf/1710.09829.pdf

Geoffrey Hinton的胶囊网络（Capsule Network）一经发布就震动了整个人工智能领域，它将卷积神经网络（CNN）的极限提升到一个新的水平。这种网络基于一种被Hinton称为胶囊（capsule）的结构。 此外，他还发表了囊间动态路由算法，用来训练新提出的胶囊网络。让我们一起来看看他的这种网络结构和原理。 

卷积神经网络不足之处

• 1.卷积网络需要大量的数据来泛化
• CNN（卷积神经网络）的表现是如此优异，以至于深度学习现在如此流行。但是把检测目标的平移，旋转，加上边框等干扰会被CNN识别成其他目标，列如CNN会认为下图的三个R是不同的字母，如果使用暴力方法，把各个角度的样本都囊括进去，这样使得CNN所需的训练集要变得很大，而数据增强技术虽然有用，但提升有限，无法从根本上解决问题。
• 2.卷积网络在人类视觉系统上的表现很差
• 让我们再考虑一个非常简单的例子。如下图，如果有一张脸，那么它是由哪些特征构成的？椭圆的轮廓、眼睛、鼻子和一个嘴巴。CNN可以轻而易举地检测到这些特征，并且因此认为它检测到的是脸。但是当你用CNN去识别右边这张脸(眼睛和嘴巴位置改变了)依然会得到同样的结果。这是因为CNN识别脸时，仅仅只识别脸的几个特征部分，右图中的确有两个眼睛，一个鼻子，一张嘴，虽然位置不对，但是CNN一旦检测到这些特征，那么识别结果是就是脸， CNN是不会注意子结构之间关系的。

究其原因是CNN的主要部分是卷积层，用于检测图像像素中的重要特征。较深的层（更接近输入的层）将学习检测诸如边缘和颜色渐变之类的简单特征，而较高的层则将简单特征组合成复杂一些的特征。最后，网络顶部的致密层组合高层特征并输出分类预测。

但凡对CNN有所了解都知道，低层特征通过加权组合成高层特征。不过在这个过程中，组成高层特征的低层特征之间并不存在位姿（平移和旋转）关系。为了解决这个问题，CNN通过后接最大池化层或者后续卷积层。这样不仅能减少参数，还能增加网络神经元的视野，检测更大区域的特征来弥补，如此达到的效果在某些领域甚至能超越人类。但是Hinton自己就表示，卷积神经网络使用的池化操作是一个巨大的错误，它表现地如此优异则是一场灾难。不仅如此还有一个关键问题：卷积神经网络的内部数据表现出它不能形成简单和复杂对象之间的重要空间层级。就如上面的例子，图片中存在两只眼睛、一张嘴和一个鼻子，仅仅这些并不意味着图片中存在一张脸，还需要考虑这些对象彼此之间的朝向关系。

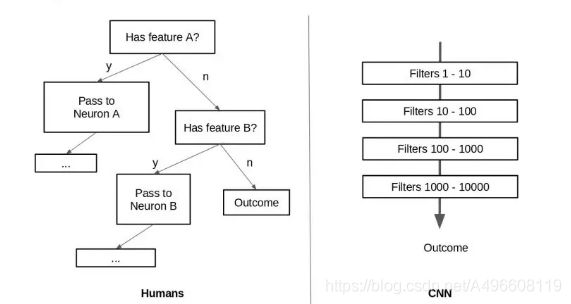
不仅如此，Hinton认为的人与CNN神经网络的最大区别：人类在识别图像的时候，是遵照树形的方式，由上而下展开式的，而CNN则是通过一层层的过滤，将信息一步步由下而上的进行抽象。

总的来说：

正因为卷积神经网络神经元之间都是平等的，缺少一种内部结构，所以对不同位置、角度下的同一个物品可能做出不同识别，更无法表现子结构之间的关系。CNN中采用的分块和共享权重的方法，以使其够使神经网络学到的特征提取能够在图形出现微小变化时能够应对，而不是针对图形的变化，对应神经网络进行相应的改变，而这正是capsule神经网络所要做的。

位姿

Hinton主张，为了正确地分类和辨识对象，保留对象部件间的分层位姿关系很重要。这是让你理解胶囊理论为何如此重要的关键所在，它结合了对象之间的相对关系，在数值上表示为4维位姿矩阵。所以我们要在神经网络中尝试建立位姿关系，在三维图形中，三维对象之间的关系可以用位姿表示，位姿的本质是平移和旋转 当在神经网络里面构建了这些关系之后，模型就能非常容易理解他看到的是以前的东西，只不过是另一个视角而已。从下面的图片中你可以轻易辨识出这是自由女神像，尽管所有的图像显示的角度都不一样。这是因为你脑中的自由女神像的内部表示并不依赖视角。你大概从没有见过和这些一模一样的图片，但你仍然能立刻知道这是自由女神像。

但是对CNN而言，这个任务非常难，因为它没有内建对三维空间的理解。而对于胶囊神经网络而言，这个任务要容易得多，因为它显式地建模了这些关系。相比之前最先进的方法，使用CapsNet的论文能够将错误率降低，这是一个巨大的提升。胶囊方法的另一大益处在于，相比CNN需要的数据，它只需要学习一小部分数据，就能达到最先进的效果（Hinton在他关于CNN错误的著名演说中提到了这一点）。 从这个意义上说，胶囊理论实际上更接近人脑的行为。为了学会区分数字，人脑只需要几十个例子，最多几百个例子。而CNN则需要几万个例子才能取得很好的效果。这看起来像是在暴力破解，显然要比我们的大脑低级。

下图为胶囊神经网络的位姿辨别效果

和其他模型相比，胶囊网络在辨识上一列和下一列的图片属于同一类、仅仅视角不同方面，表现要好很多，相对于CNN这是压倒性的优势

胶囊是什么？

让我们先看看Hinton等人的《Transforming Autoencoders》中关于胶囊的描述：

人工神经网络不应当追求“神经元”活动中的视角不变性（使用单一的标量输出来总结一个局部池中的重复特征检测器的活动），而应当使用局部的“胶囊”，这些胶囊对其输入执行一些相当复杂的内部计算，然后将这些计算的结果封装成一个包含信息丰富的输出的小向量。每个胶囊学习辨识一个**有限的观察条件和变形范围内隐式定义的视觉实体**，并输出实体在有限范围内存在的概率及一组“实例参数”，实例参数可能包括相对这个视觉实体的隐式定义的典型版本的精确的位姿、照明条件和变形信息。当胶囊工作正常时，视觉实体存在的概率具有局部不变性——当实体在胶囊覆盖的有限范围内的外观流形上移动时，概率不会改变。实例参数却是“等变的”——随着观察条件的变化，实体在外观流形上移动时，实例参数也会相应地变化，因为实例参数表示实体在外观流形上的内在坐标。

阅读上面这段话我们可以很好理解到，人造神经元输出单个标量表示结果，而胶囊可以输出向量作为结果，CNN（卷积神经网络）使用卷积层获取特征矩阵，为了在神经元的活动中实现视角不变性。我们通过最大池化方法来达成这一点。最大池化持续地搜寻二维特征矩阵的区域，以选取每个区域中最大的数字作为输出结果。如果我们略微调整输入，在输入图像上，我们稍微变换一下我们想要检测的对象时，由于最大池化保持不变，网络仍然能检测到对象。

使用最大池的缺点就是丢失了有价值的信息，也没能处理特征之间的相对空间关系。但是胶囊检测中的特征的状态的重要信息，都将以向量的形式被胶囊封装。

胶囊将特征检测的概率作为其输出向量的长度进行编码。检测出的特征的状态被编码为该向量指向的方向。所以，当检测出的特征在图像中移动或其状态不知怎的发生变化时，概率仍然保持不变（向量长度没有改变），但它的方向改变了。想象一个胶囊，它检测图像中的面部，并输出长度小于1的三维向量。接着我们开始在图像上移动面部。向量将在空间上旋转，表示检测出的面部的状态改变了，但其长度（检测概率）仍然保持，这使胶囊仍然确信它检测出到了面部。这就是Hinton所说的活动等变性：这才是我们应该追求的那种不变性，而不是CNN提供的基于最大池化的不变性。

胶囊的工作原理

让我们比较下胶囊与人造神经元。下表中Vector表示向量，scalar表示标量，Operation中对比了它们工作原理的差异。

图中Vector表示向量，scalar表示标量，Operation中对比了它们的不同工作原理

人造神经元可以用3个步骤来表示：

1. 输入标量的标量加权

2. 加权输入标量之和

3. 标量到标量的非线性变换

胶囊具有上面3个步骤的向量版，并新增了输入的仿射变换这一步骤：

   1.输入向量的矩阵乘法

   2.输入向量的标量加权

   3.加权输入向量之和

   4.向量到向量的非线性变换

1.输入向量的矩阵乘法

胶囊接收的输入向量（上图中的U1、U2和U3）来自下层的3个胶囊。这些向量的长度分别编码下层胶囊检测出的相应特征的概率，向量的方向则编码检测出的特征的一些内部状态。让我们假定下层的胶囊分别检测眼睛、嘴巴和鼻子，而输出胶囊检测面部。接着将这些向量乘以相应的权重矩阵W，W编码了低层特征（眼睛、嘴巴和鼻子）和高层特征（面部）之间的空间关系和其他重要关系。乘以这些矩阵后，我们得到的是高层特征的状态（位置，方向，大小等）

你也可以理解为：

• û1表示根据检测出的眼睛的位置，面部应该在什么位置，
• û2表示根据检测出的嘴巴的位置，面部应该在什么位置，
• û3表示根据检测出的鼻子的位置，面部应该在什么位置。如果这3个胶囊输出对象（面部）位置相同，那么就可以将这3个输出编码出一个更高层的特征(同时关于眼睛、嘴巴、鼻子、面部的关系特征）

2.输入向量的标量加权

• 一个底层胶囊搞如何把信息输出给高级胶囊呢

之前的人造神经元是通过反向传播算法一步步调整权重优化网络，而胶囊则有所不同

上图中，左右分别是高层的两个不同胶囊，方形区域内的点则是下层胶囊输入在这个胶囊的分布，一个低层胶囊需要“决定”将它的输出发送给哪个高层胶囊。它将通过调整权重C做出决定，胶囊在发送输出前，先将输出乘以这个权重。胶囊将决定是把输出发给左边的胶囊J，还是发给右边的胶囊K。

关于权重，我们需要知道：

1. 权重均为非负标量（因为经过softmax函数加权）。

2. 对每个低层胶囊i而言，所有权重的总和等于1（因为经过softmax函数加权）。

3. 对每个低层胶囊i而言，权重的数量等于高层胶囊的数量。

4. 这些权重的数值由迭代动态路由算法确定。

对于每个低层胶囊i而言，其权重定义了传给每个高层胶囊j的输出的概率分布。许多个低层胶囊通过加权把向量输入高层胶囊，同时高层胶囊就会接收到来自其他低层胶囊的许多向量。所有这些输入以红点和蓝点表示。这些点聚集的地方，意味着低层胶囊的预测互相接近。比如，胶囊J和K中都有一组聚集的红点，因为那些胶囊的预测很接近。所以，一个低层胶囊该把它的输出发给胶囊J还是胶囊K呢？这个问题的答案正是动态路由算法的精髓。低层胶囊的输出乘以相应的矩阵W后，落在了远离胶囊J中的红色聚集区的地方，另一方面，在胶囊K中，它落在红色聚集区边缘，红色聚集区表示了这个高层胶囊的预测结果。低层胶囊具备测量哪个高层胶囊更能接受其输出的机制，并据此自动调整权重，使对应胶囊K的权重C变高，对应胶囊J的权重C变低。

3.加权输入向量之和

这一步骤表示输入的组合，和通常的人工神经网络差不多，除了它是向量的和而不是标量的和

4. 向量到向量的非线性变换

CapsNet的另一大创新是新颖的非线性激活函数，这个函数接受一个向量，然后在不改变方向的前提下，压缩它的长度到1以下。

• ▲||Sj||表示模长

• 上面这个公式：向量经过转换之后小于1个单位向量

• 方向不变(对单位向量长度缩放）

• 原来向量模越大，经过激活函数后的模长越接近1

囊间动态路由算法(精髓所在）

• 低层胶囊将其输出发送给对此表示“同意”的高层胶囊。这是动态路由算法的精髓。

▲囊间动态路由算法伪代码

• 伪代码的第一行指明了算法的输入：低层输入向量经过矩阵乘法得到的û，以及路由迭代次数r。最后一行指明了算法的输出，高层胶囊的向量vj。

• 第2行的bij是一个临时变量，存放了低层向量对高层胶囊的权重，它的值会在迭代过程中逐个更新，当开始一轮迭代时，它的值经过softmax转换成cij。在囊间动态路由算法开始时，bij的值被初始化为零(但是经过softmax后会转换成非零且各个权重相等的cij)。

#路由分配权重 b_ij的初始化
#u_hat_num:低层向量数目
#cap_num:高层胶囊数目
B_ij = fluid.layers.ones((1,u_hat_num,cap_num,1),dtype='float32')/cap_num

• 第3行表明第4-7行的步骤会被重复r次（路由迭代次数）。

• 第4行计算低层胶囊向量i的对应所有高层胶囊的权重。bi的值经过softmax后会转换成非零权重ci且其元素总和等于1。

#softmax过程
C_ij = fluid.layers.softmax(B_ij,axis=2)

• 如果是第一次迭代，所有系数cij的值会相等。例如，如果我们有8个低层胶囊和10个高层胶囊，那么所有cij的权重都将等于0.1。这样初始化使不确定性达到最大值：低层胶囊不知道它们的输出最适合哪个高层胶囊。当然，随着这一进程的重复，这些均匀分布将发生改变。

• 第5行，那里将涉及高层胶囊。这一步计算经前一步确定的路由系数ci加权后的输入向量的总和，得到输出向量sj。

#使用元素逐一乘算加权，比如(1,1152,1,1)*(32,1152,16,1)-->（32,1152，16,1）每16个向量分配一个权重
v_j = fluid.layers.elementwise_mul(u_hat,c_ij)
#将分配到这一个胶囊的向量相加得到v_j:(32,1,16,1)的输出
v_j = fluid.layers.reduce_sum(v_j,dim=1,keep_dim=True)

• 第6行，来自前一步的向量将穿过squash非线性函数，反向不变，长度被归一化至1以下。

v_j = self.squash(v_j) 

• 第7行进行更新权重，这是路由算法的精髓所在。我们将每个高层胶囊的向量vj与低层原来的输入向量û逐元素相乘求和获得内积（也叫点积，点积检测胶囊的输入和输出之间的相似性（下图为示意图）），再用点积结果更新原来的权重bi。这就达到了’低层胶囊将其输出发送给具有类似输出的高层胶囊’的效果，点积刻画了向量之间的相似性。这一步骤之后，算法跳转到第3步重新开始这一流程，并重复r次。

#平铺v_j (32,1,16,1)-->(32,1152,16,1) 因为这要对1152个不同向量进行计算
v_j_expand = fluid.layers.expand(v_j,(1,pre_cap_num,1,1))
#求内积 也是逐一元素相乘算，然后求和 #(32,1152,16,1)-->(32,1152,1,1)
u_v_produce = fluid.layers.elementwise_mul(u_hat,v_j_expand)
u_v_produce = fluid.layers.reduce_sum(u_v_produce,dim=2,keep_dim=True)
#内积累加(把bach_size的累加到一块)，更新路由权重BIJ
b_ij += fluid.layers.reduce_sum(u_v_produce,dim=0,keep_dim=True)

▲点积运算即为向量的内积（点积）运算，可以表现向量的相似性,点积运算接收两个向量，并输出一个标量。对于给定长度但方向不同的两个向量而言，点积有几种情况： a正值（夹角小于90°）；b零（夹角垂直）；c负值（夹角大于180°）

上图中，两个高层胶囊的输出用向量v1和v2表示。橙色向量表示接收自某个低层胶囊的输入，其他黑色向量表示接收自其他低层胶囊的输入。

我们看到，左边的输出v1和橙色输入û1|1指向相反的方向，它们并不相似。这意味着它们的点积将是一个负数，与bi相加后值变小，并减少路由系数c11(见伪代码第7层）。右边的输出v2和橙色输入û2|1指向相同的方向，它们是相似的，所以，路由系数c12会增加。经过路由迭代计算，得到一个路由系数的集合，使来自低层胶囊的输出与高层胶囊的输出的最佳匹配。

重复r次后，我们计算出了所有高层胶囊的输出，并确立正确路由权重。

损失函数

训练时，对于每个训练样本，根据下面的公式计算每个胶囊向量的损失值，然后将10个损失值相加得到最终损失。这是一个监督学习，所以每个训练样本都有正确的标签，在这种情况下，它将是一个10维one-hot编码向量，该向量由9个零和1个一（正确标签）组成。在损失函数公式中，与正确的标签对应的输出胶囊，系数Tc为1

如果正确标签是9，这意味着第9个胶囊输出的损失函数的Tc为1，其余9个为0。

       当Tc为1时，公式中损失函数的右项系数为零，也就是说正确输出项损失函数的值只包含了左项计算。相应的左系数为0则右项系数为1，错误输出项损失函数的值只包含了右项计算。

       |v|为胶囊输出向量的模长，一定程度上表示了类概率的大小，我们再拟定一个量m+，用这个变量来衡量概率是否合适，将m+与|v|作差，即得到了左项中的公式，正确输出项的概率（|v|）大于这个值则loss为0，越接近则loss越小。

       同样的，将m-与|v|作差，即得到了右项中的公式错误输出项的概率，（|v|）小于这个值则loss为0，越接近则loss越小，公式右项包括了一个lambda系数以确保训练中的数值稳定性（lambda为固定值0.5），这两项取平方是为了让损失函数符合L2正则。

编码器

完整的网络结构分为编码器和解码器，我们先来看看编码器

1.输入图片28x28首先经过1x256x9x9的卷积层 获得256个20x20的特征图

2.然后再用8组256x32x9x9(stride=2)的卷积获得8组32x6x6的特征图

3.之后将获取的特征图向量化输入10个胶囊，这10个胶囊输出向量的长度就是各个类别的概率

我们不难看出特征图转换成向量实际的过程是将每组二维矩阵展开成一维矩阵（当然有多个二维矩阵则展开后前后拼接） 之后再将所有组的一维矩阵在新的维度拼接形成向量（下图为示意图）

当然向量化的方法我认为可以有所改进：

1.这8个32x9x9的卷积组如果换成1个256x9x9的卷积不是一样吗，为何要分开来？

根据这个疑问我把8个卷积组合成一个卷积层，后面直接reshape成向量

结果发现网络就这么失效了。然后我转变思路不用reshape，而是用split把特征图分组之后用for循环拼接，网络又有效了，也加快了速度。

2.虽然已经把8次卷积缩小到了一次卷积，但是仍然使用的for循环，在循环次数过多的情况下运行效率会变慢。

经过思索发现只用split和concat方法也可以直接向量化。

解码器

       解码器从正确的胶囊中接受一个16维向量，并学习将其解码为数字图像（它在训练时仅使用正确的胶囊向量，忽略不正确的）。解码器被用来作为正则子，它接受正确胶囊的输出作为输入，并学习重建一张28×28像素的图像，损失函数为重建图像与输入图像之间的欧氏距离。解码器强制胶囊学习对重建原始图像有用的特征。重建图像越接近输入图像越好。

下图是我自己训练的网络重构获得的图像，上面是输入网络的原图片，下面是网络输出rebuild的图片

性能评估

说了这么多胶囊神经网络性能到底如何呢，让我们用同规模CNN+最大池化层来对比下对比一下

这是两个网络在其他条件相同情况下进行的1800次迭代，一开始胶囊神经网络起步慢，但是结果很明显胶囊神经网络更加稳定，CNN+池化层准确率波动不小

再来试一下，当训练到一半时将所有输入网络的图片转置（你可以理解为将数字翻转，改变位姿）的情况

• 可以明显的看到CNN+池化层在图片转置的情况下准确率直接跌落谷底，在之后的训练中也是一蹶不振（迷失了自我）！

• 但是胶囊神经网络就不一样了，面对截然不同的图片仍然有高于50%的正确率，而且在之后迅速恢复了100%的正确率！甩了CNN+池化层一大截！Capsule显露了它处理不同位姿的本领！

胶囊数量和向量维度对性能的影响