二叉树的先序创建递归遍历和非递归遍历和求叶子结点和树的高度等操作c语言
效果图如下
下面为内容:
源文件:
#include "层次遍历的Queue.h"
#include "非递归算法的堆栈.h"
void Create(BinaryTree* bt) //构造一棵空的二叉树
{
bt->root = NULL;
}
BTNode* NewNode(ElemType x, BTNode* ln, BTNode* rn) //创造一个新的节点
{
BTNode* p = (BTNode*)malloc(sizeof(BTNode));
p->element = x;
p->lChild = ln;
p->rChild = rn;
return p;
}
void MakeTree(BinaryTree* bt, ElemType e, BinaryTree* left, BinaryTree* right)
{
if (bt->root || left == right)
return;
bt->root = NewNode(e, left->root, right->root);
left->root = right->root = NULL;
}
BOOL ROOT(BinaryTree* bt, ElemType* x) //若二叉树非空,则得到其根节点的值,返回true,否则返回false
{
if (bt->root)
{
x = &bt->root->element;
return true;
}
else
return false;
}
// 先序遍历二叉树
void PreOrder(BTNode* t)
{
if (!t)
return;
printf("%c ", t->element);
PreOrder(t->lChild);
PreOrder(t->rChild);
}
void PreOrderTree(BinaryTree* bt)
{
printf("\n先序遍历二叉树的结果为:\n");
PreOrder(bt->root);
}
//中序遍历二叉树
void InOrder(BTNode* t)
{
if (!t)
return;
InOrder(t->lChild);
printf("%c ", t->element);
InOrder(t->rChild);
}
void InOrderTree(BinaryTree* bt)
{
printf("\n中序遍历二叉树的结果为:\n");
InOrder(bt->root);
}
//后续遍历二叉树
void PostOrder(BTNode* t)
{
if (!t)
return;
PostOrder(t->lChild);
PostOrder(t->rChild);
printf("%c ", t->element);
}
void PostOrderTree(BinaryTree* bt)
{
printf("\n后序遍历二叉树的结果为:\n");
PostOrder(bt->root);
}
//清空二叉树
void Clear(BTNode* t)
{
if (t)
return;
Clear(t->lChild);
Clear(t->rChild);
free(t);
}
void TreeClear(BinaryTree* bt)
{
Clear(bt->root);
}
//求二叉树的节点数
int Size(BTNode* t)
{
if(!t)
return 0;
else
{
return Size(t->lChild) + Size(t->rChild) + 1;
}
}
int TreeSize(BinaryTree* bt)
{
return Size(bt->root);
}
//层次遍历二叉树
void LevelOrderTree(BinaryTree* tree)
{
printf("\n层次遍历的结果如下:\n");
ElemType element;
if (!tree->root)
return;
Queue Q;
queuecreate(&Q, QUEUESIZE);
BTNode* p = tree->root;
BinaryTree h, i, j;
Create(&h);
Create(&i);
Create(&j);
MakeTree(&h, 'H', &i, &j);
BTNode* q = h.root;
EnQueue(&Q, p);
while (!queueIsEmpty(&Q))
{
queueFront(&Q, q);
DeQueue(&Q);
printf("%c ", q->element);
if (q->lChild)
EnQueue(&Q, q->lChild);
if (q->rChild)
EnQueue(&Q, q->rChild);
}
queueDestory(&Q);
}
//先序遍历构建二叉树
BTNode *PreCreateBT(BTNode* t)
{
char ch;
ch = getchar(); //输入先序规则下当前子树根节点的元素
if (ch == '#')
t = NULL;
else
{
t = (BTNode*)malloc(sizeof(BTNode));
t->element = ch;
t->lChild = PreCreateBT(t->lChild);
t->rChild = PreCreateBT(t->rChild);
}
return t;
}
void PreMakeTree(BinaryTree* bt)
{
printf("\n请输入先序排列的树的顺序:\n");
bt->root = PreCreateBT(bt->root);
}
//二叉树遍历的非递归算法
/*递归是程序设计中强有力的工具。递归函数结构清晰,使程序易读。但递归函数也有不可克服的弱点,时间,空间效率较低,运行代价较高。*/
//非递归先序遍历二叉树的算法
void PreTraverse(BinaryTree* bt)
{
Stack S;
stackCreate(&S, STACKSIZE);
printf("\n非递归先序遍历算法结果如下:\n");
BTNode* p;
BTNode* temp;
BinaryTree h, i, j;
Create(&h);
Create(&i);
Create(&j);
MakeTree(&h, 'H', &i, &j);
temp = h.root;
p = bt->root;
if (!p)
return;
stackPush(&S, p);
while (S.top != -1)
{
stackTOP(&S, temp);
stackPop(&S);
printf("%c ", temp->element);
if (temp->rChild != NULL)
stackPush(&S, temp->rChild);
if (temp->lChild != NULL)
{
stackPush(&S, temp->lChild);
}
}
}
/*
非递归终须遍历算法的执行步骤如下:
(1)调用GetFirst函数获取二叉树的最左后裔节点(如果存在的话),并将该节点设置为当前待访问节点;
(2)只要当前带访问节点存在,则访问该节点,然后调用函数GetNext获取该节点在中序遍历下的直接后继节点,并作为新的当前待访问节点,继续循环执行步骤(2)
GetFirst 函数用于后驱二叉树的根节点和最左后裔节点,并使得从根节点到该最左后裔节点的路径中的所有节点(最左后裔节点除外)依次进栈。而GetNext函数则用于获取当前访问节点的中序遍历下的直接后继节点
具体实现算法如下:
*/
BTNode* InGetFirst(BinaryTree* bt, Stack* S) //该函数负责付汇当前遍历次序下的被访问的节点,若二叉树为空,则返回NULL
{
BTNode* p = bt->root;
if (!p)
return NULL;
while (p->lChild != NULL)
{
stackPush(S, p);
p = p->lChild;
}
return p;
}
BTNode* InGetNext(BTNode* current, Stack* S)//该函数负责返回当前遍历次序下的被访问节点current的后继节点,如果后继节点不存在,则返回NULL
{
BTNode* p;
BTNode* temp;
BinaryTree h, i, j;
Create(&h);
Create(&i);
Create(&j);
MakeTree(&h, 'H', &i, &j);
temp = h.root;
if (current->rChild != NULL)
{
p = current->rChild;
while (p->lChild != NULL)
{
stackPush(S, p);
p = p->lChild;
}
current = p;
}
else if (!stackIsEmpty(S))
{
stackTOP(S, temp);
stackPop(S);
return temp;
}
else
{
current = NULL;
}
return current;
}
void InTraverse(BinaryTree* bt) // 该函数利用循环结构非递归地访问二叉树bt中的每个节点
{
printf("\n非递归方法中序遍历二叉树方法如下:\n");
Stack S;
BTNode* current;
stackCreate(&S, STACKSIZE);
current = InGetFirst(bt, &S);
while (current)
{
printf("%c ", current->element);
current = InGetNext(current, &S);
}
printf("\n");
}
// 非递归方式后序遍历二叉树算法
BTNode* PostGetFirst(BinaryTree* tree, Stack* S)
{
BTNode* p = tree->root;
if (!p)
return NULL;
while (p->lChild != NULL)
{
stackPush(S, p);
p = p->lChild;
}
return p;
}
BTNode* PostGetNext(BTNode* current, Stack* S)
{
BTNode* p;
BTNode* temp;
BinaryTree h, i, j;
Create(&h);
Create(&i);
Create(&j);
MakeTree(&h, 'H', &i, &j);
temp = h.root;
p = current;
if (p->rChild&&p->judge!=1)
{
p->judge = 1;
stackPush(S, p);
p = p->rChild;
while (p->lChild)
{
stackPush(S, p);
p = p->lChild;
}
current = p;
return p;
}
else if (!stackIsEmpty(S))
{
stackTOP(S, temp);
stackPop(S);
if (temp->rChild && temp->judge != 1)
{
temp->judge = 1;
stackPush(S, temp);
temp = temp->rChild;
while (temp->lChild)
{
stackPush(S, temp);
temp = temp->lChild;
}
}
current = temp;
}
else
{
return NULL;
}
return current;
}
void PostTraverse(BinaryTree* tree)
{
printf("非递归方式后续遍历二叉树算法:\n");
Stack S;
stackCreate(&S, STACKSIZE);
BTNode* current;
current = PostGetFirst(tree, &S);
while (current)
{
printf("%c ", current->element);
current = PostGetNext(current, &S);
}
printf("\n");
}
//求二叉树总结点个数的算法:
int AllSize(BTNode* t)
{
if (!t)
return 0;
else
return AllSize(t->lChild) + AllSize(t->rChild) + 1;
}
int TreeAllSize(BinaryTree* bt)
{
return AllSize(bt->root);
}
//求非二叉树叶节点的个数的算法:
int YeSize(BTNode* t)
{
if (!t)
{
return 0;
}
else if ((t->lChild == NULL) || (t->rChild == NULL))
{
return 0;
}
else
{
return YeSize(t->lChild) + YeSize(t->rChild) + 1;
}
}
int TreeFeiYeSize(BinaryTree* bt)
{
return YeSize(bt->root);
}
//求二叉树高度的算法
int GetHeight(BTNode* t)
{
int hl, hr, max = 0;
if (t != NULL)
{
hl = GetHeight(t->lChild);
hr = GetHeight(t->rChild);
max = hl > hr ? hl : hr;
return (max + 1);
}
else
return 0;
}
int GetHeightTree(BinaryTree* bt)
{
return GetHeight(bt->root);
}
// 交换二叉树所有左右子树的操作
void Change(BTNode* t)
{
BTNode* temp = (BTNode*)malloc(sizeof(BTNode));
if (t)
{
if (t == NULL)
return;
else
{
temp = t->lChild;
t->lChild = t->rChild;
t->rChild = temp;
Change(t->lChild);
Change(t->rChild);
}
}
}
void ChangeTree(BinaryTree* bt)
{
Change(bt->root);
}
void main()
{
BinaryTree a, b, c, e, d, f,g,h,i,j,x,y;
Create(&c);
Create(&a);
Create(&b);
Create(&c);
Create(&d);
Create(&e);
Create(&f);
Create(&g);
Create(&h);
Create(&i);
Create(&x);
Create(&y);
MakeTree(&d, 'D', &h, &i);
MakeTree(&e, 'E', &h, &i);
MakeTree(&b, 'B', &d, &e);
MakeTree(&f, 'F', &h, &i);
MakeTree(&g, 'G', &h, &i);
MakeTree(&c, 'C', &f, &g);
MakeTree(&a, 'A', &b, &c);
MakeTree(&y, 'Y', &h, &i);
MakeTree(&x, 'X', &a, &y);
int size = TreeSize(&x); //计算二叉树的总结点
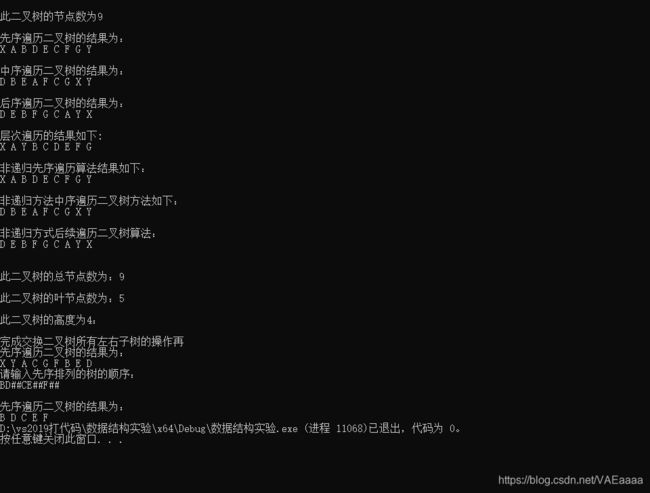
printf("\n此二叉树的节点数为%d\n", size);
PreOrderTree(&x); //递归先序遍历
printf("\n");
InOrderTree(&x); //递归中序遍历
printf("\n");
PostOrderTree(&x); // 递归后序遍历
printf("\n");
LevelOrderTree(&x); //使用队列层次遍历
printf("\n");
PreTraverse(&x); //非递归算法先序遍历二叉树
printf("\n");
InTraverse(&x); //非递归算法中序遍历二叉树
printf("\n");
PostTraverse(&x); //非递归算法后序遍历二叉树
printf("\n");
int AllSize = TreeAllSize(&x);
printf("\n此二叉树的总节点数为:%d\n", AllSize);
//求叶节点思想:求非叶节点的算法较容易,则求出非叶节点个数,再求出总节点个数,用总结点个数减去非叶节点个数,得到叶节点个数
int YeSize = TreeFeiYeSize(&x);
printf("\n此二叉树的叶节点数为:%d\n", AllSize - YeSize);
printf("\n此二叉树的高度为%d:\n\n", GetHeightTree(&x));
ChangeTree(&x);
printf("完成交换二叉树所有左右子树的操作再");
PreOrderTree(&x);
PreMakeTree(&c); //先序遍历顺序构造二叉树
PreOrderTree(&c);
TreeClear(&c);
TreeClear(&x);
}
层次遍历的Queue.h:
#pragma once
#include "BTNODE.h"
#define QUEUESIZE 100
typedef struct Queue
{
int front;
int rear;
int maxSize;
BTNode* element;
}Queue;
//创建一个能容纳mSize个单元的空队列
void queuecreate(Queue* Q, int mSize)
{
Q->maxSize = mSize;
Q->element = (BTNode*)malloc(sizeof(BTNode) * mSize);
Q->front = Q->rear = 0;
}
//小会一个已存在的队列,即释放队列占用的数组空间
void queueDestory(Queue* Q)
{
Q->maxSize = 0;
Q->front = Q->rear = -1;
free(Q->element);
}
//判断队列是否为空,若是,则返回true;否则返回false
BOOL queueIsEmpty(Queue* Q)
{
return Q->front == Q->rear;
}
//判断堆栈是否已满,若是,则返回true,否则返回true
BOOL queueIsFull(Queue* Q)
{
return (Q->rear + 1) % Q->maxSize == Q->front;
}
//获取队头元素,并通过x返回,若操作成功,则返回true,否则返回false
BOOL queueFront(Queue* Q, BTNode* x)
{
if (queueIsEmpty(Q))
return false;
*x = Q->element[(Q->front + 1) % Q->maxSize];
return true;
}
//从队列Q的队尾插入元素x(入队操作)。操作成功,则返回true,否则返回false
BOOL EnQueue(Queue* Q, BTNode *x)
{
if (queueIsFull(Q))
return false;
Q->rear = (Q->rear + 1) % Q->maxSize;
Q->element[Q->rear] = *x;
return true;
}
//从队列Q中删除队头元素(出队操作)。操作成功,则返回true,否则返回false
BOOL DeQueue(Queue* Q)
{
if (queueIsEmpty(Q))
return false;
Q->front = (Q->front + 1) % Q->maxSize;
return true;
}
//清除队列中全部元素,是队列恢复初始状态,但并不释放空间
void queueClear(Queue* Q)
{
Q->front = Q->rear = 0;
}
非递归算法的堆栈.h:
#pragma once
#include## BTNODE.h:
#pragma once
#include