柳叶刀与小鼠标
柳叶刀与小鼠标

R语言之可视化（31）扫地僧easystats（2）相关性分析

R语言之可视化（30）扫地僧easystats（1）

介绍

相关性是一个专注于相关性分析的easystats软件包。 它轻巧，易于使用，并允许计算许多不同类型的相关性，例如偏相关性，贝叶斯相关性，多级相关性，或Sheperd的Pi相关性（鲁棒相关性的类型），距离相关（一种非线性相关性）等等，还允许它们之间进行组合（例如，贝叶斯局部多级相关性）。

不同的相关方法

  • Pearson’s correlation：两个变量的协方差除以其标准偏差的乘积。
  • Spearman’s rank correlation：等级相关性的非参数度量（两个变量的等级之间的统计相关性）。两个变量>之间的Spearman相关性等于这两个变量的等级值之间的Pearson相关性；皮尔森的相关性评估线性关系，而>斯皮尔曼的相关性评估单调关系（无论线性与否）。
  • Kendall’s rank correlation：在正常情况下，肯德尔相关性比Spearman相关性更可取，因为它的总差错敏感度（GES）较小，而渐近方差（AV）较小，从而使其更健壮和更有效。但是，从某种意义上说，肯德尔的tau的解释比斯皮尔曼的rho的解释不那么直接，因为它可以量化所有可能的成对事件中一致和不一致对的百分比之间的差异。
  • Biweight midcorrelation：基于中位数而不是基于均值的样本之间相似度的一种度量，因此对异常值不那么敏感，并且可以作为其他相似度度量（例如Pearson相关）的可靠替代。
  • Distance correlation距离相关：距离相关可测量两个随机变量或随机矢量之间的线性和非线性关联。这与Pearson的相关性相反，后者只能检测两个随机变量之间的线性关联。
  • Percentage bend correlation折弯百分比相关性：Wilcox（1994）引入的折弯相关性是基于特定百分比的边际观测值的权重偏低（偏离默认值20％）而得出的。
  • Shepherd’s Pi correlation关联：等同于剔除异常值后的Spearman等级关联（通过自举马氏距离）。
  • Multilevel correlation多级相关：多级相关是部分相关的一种特殊情况，其中要调整的变量是一个因素，并作为随机效应包含在混合模型中。

安装和加载包


devtools::install_github("easystats/correlation")

library(correlation)
library(bayestestR)
library(see)

library(ggplot2)
library(tidyr)
library(dplyr)



cor <- correlation(iris)
cor
Parameter1   |   Parameter2 |     r |         95% CI |     t |  df |      p |  Method | n_Obs
---------------------------------------------------------------------------------------------
Sepal.Length |  Sepal.Width | -0.12 | [-0.27,  0.04] | -1.44 | 148 | 0.152  | Pearson |   150
Sepal.Length | Petal.Length |  0.87 | [ 0.83,  0.91] | 21.65 | 148 | < .001 | Pearson |   150
Sepal.Length |  Petal.Width |  0.82 | [ 0.76,  0.86] | 17.30 | 148 | < .001 | Pearson |   150
Sepal.Width  | Petal.Length | -0.43 | [-0.55, -0.29] | -5.77 | 148 | < .001 | Pearson |   150
Sepal.Width  |  Petal.Width | -0.37 | [-0.50, -0.22] | -4.79 | 148 | < .001 | Pearson |   150
Petal.Length |  Petal.Width |  0.96 | [ 0.95,  0.97] | 43.39 | 148 | < .001 | Pearson |   150

Parameter1 为列1， Parameter2为列2，从上面表格我们可以出看出一些必要的相关信息，包括相关系数r，P值、相关检验的方法Method和观察值数量。

summary(cor)
Parameter    | Petal.Width | Petal.Length | Sepal.Width
-------------------------------------------------------
Sepal.Length |     0.82*** |      0.87*** |       -0.12
Sepal.Width  |    -0.37*** |     -0.43*** |            
Petal.Length |     0.96*** |              |

通过数据框的形式来展示

> summary(cor, redundant = TRUE)
Parameter    | Sepal.Length | Sepal.Width | Petal.Length | Petal.Width
----------------------------------------------------------------------
Sepal.Length |      1.00*** |       -0.12 |      0.87*** |     0.82***
Sepal.Width  |        -0.12 |     1.00*** |     -0.43*** |    -0.37***
Petal.Length |      0.87*** |    -0.43*** |      1.00*** |     0.96***
Petal.Width  |      0.82*** |    -0.37*** |      0.96*** |     1.00***

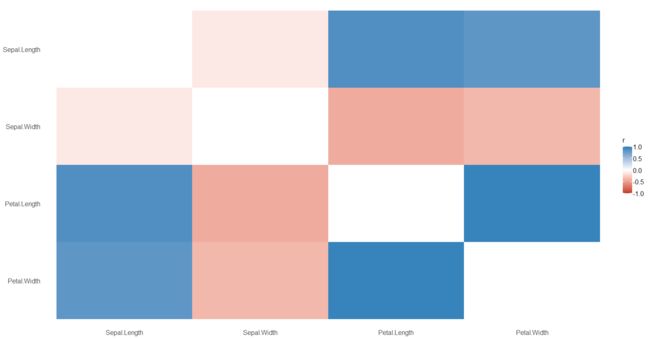
绘图


library(dplyr)
library(see)

cor %>% 
  summary( redundant = TRUE) %>% 
  plot()
R语言之可视化（31）扫地僧easystats（2）相关性分析_第1张图片

分组后相关分析

> iris %>% 
+   select(Species, Sepal.Length, Sepal.Width, Petal.Width) %>% 
+   group_by(Species) %>% 
+   correlation()
Group      |   Parameter1 |  Parameter2 |    r |        95% CI |    t | df |      p |  Method | n_Obs
-----------------------------------------------------------------------------------------------------
setosa     | Sepal.Length | Sepal.Width | 0.74 | [ 0.59, 0.85] | 7.68 | 48 | < .001 | Pearson |    50
setosa     | Sepal.Length | Petal.Width | 0.28 | [ 0.00, 0.52] | 2.01 | 48 | 0.101  | Pearson |    50
setosa     |  Sepal.Width | Petal.Width | 0.23 | [-0.05, 0.48] | 1.66 | 48 | 0.104  | Pearson |    50
versicolor | Sepal.Length | Sepal.Width | 0.53 | [ 0.29, 0.70] | 4.28 | 48 | < .001 | Pearson |    50
versicolor | Sepal.Length | Petal.Width | 0.55 | [ 0.32, 0.72] | 4.52 | 48 | < .001 | Pearson |    50
versicolor |  Sepal.Width | Petal.Width | 0.66 | [ 0.47, 0.80] | 6.15 | 48 | < .001 | Pearson |    50
virginica  | Sepal.Length | Sepal.Width | 0.46 | [ 0.20, 0.65] | 3.56 | 48 | 0.002  | Pearson |    50
virginica  | Sepal.Length | Petal.Width | 0.28 | [ 0.00, 0.52] | 2.03 | 48 | 0.048  | Pearson |    50
virginica  |  Sepal.Width | Petal.Width | 0.54 | [ 0.31, 0.71] | 4.42 | 48 | < .001 | Pearson |    50
>

自动选择检验方法的相关分析

> correlation(iris, include_factors = TRUE, method = "auto")
For i = 2 j = 1  A cell entry of 0 was replaced with correct =  0.5.  Check your data!
For i = 2 j = 1  A cell entry of 0 was replaced with correct =  0.5.  Check your data!
For i = 2 j = 1  A cell entry of 0 was replaced with correct =  0.5.  Check your data!
Parameter1         |         Parameter2 |     r |         95% CI |      t |  df |      p |         Method | n_Obs
-----------------------------------------------------------------------------------------------------------------
Sepal.Length       |        Sepal.Width | -0.12 | [-0.27,  0.04] |  -1.44 | 148 | 0.452  |        Pearson |   150
Sepal.Length       |       Petal.Length |  0.87 | [ 0.83,  0.91] |  21.65 | 148 | < .001 |        Pearson |   150
Sepal.Length       |        Petal.Width |  0.82 | [ 0.76,  0.86] |  17.30 | 148 | < .001 |        Pearson |   150
Sepal.Length       |     Species.setosa | -0.72 | [-0.79, -0.63] | -12.53 | 148 | < .001 | Point-biserial |   150
Sepal.Length       | Species.versicolor |  0.08 | [-0.08,  0.24] |   0.97 | 148 | 0.452  | Point-biserial |   150
Sepal.Length       |  Species.virginica |  0.64 | [ 0.53,  0.72] |  10.08 | 148 | < .001 | Point-biserial |   150
Sepal.Width        |       Petal.Length | -0.43 | [-0.55, -0.29] |  -5.77 | 148 | < .001 |        Pearson |   150
Sepal.Width        |        Petal.Width | -0.37 | [-0.50, -0.22] |  -4.79 | 148 | < .001 |        Pearson |   150
Sepal.Width        |     Species.setosa |  0.60 | [ 0.49,  0.70] |   9.20 | 148 | < .001 | Point-biserial |   150
Sepal.Width        | Species.versicolor | -0.47 | [-0.58, -0.33] |  -6.44 | 148 | < .001 | Point-biserial |   150
Sepal.Width        |  Species.virginica | -0.14 | [-0.29,  0.03] |  -1.67 | 148 | 0.392  | Point-biserial |   150
Petal.Length       |        Petal.Width |  0.96 | [ 0.95,  0.97] |  43.39 | 148 | < .001 |        Pearson |   150
Petal.Length       |     Species.setosa | -0.92 | [-0.94, -0.89] | -29.13 | 148 | < .001 | Point-biserial |   150
Petal.Length       | Species.versicolor |  0.20 | [ 0.04,  0.35] |   2.51 | 148 | 0.066  | Point-biserial |   150
Petal.Length       |  Species.virginica |  0.72 | [ 0.63,  0.79] |  12.66 | 148 | < .001 | Point-biserial |   150
Petal.Width        |     Species.setosa | -0.89 | [-0.92, -0.85] | -23.41 | 148 | < .001 | Point-biserial |   150
Petal.Width        | Species.versicolor |  0.12 | [-0.04,  0.27] |   1.44 | 148 | 0.452  | Point-biserial |   150
Petal.Width        |  Species.virginica |  0.77 | [ 0.69,  0.83] |  14.66 | 148 | < .001 | Point-biserial |   150
Species.setosa     | Species.versicolor | -0.88 | [-0.91, -0.84] | -22.35 | 148 | < .001 |    Tetrachoric |   150
Species.setosa     |  Species.virginica | -0.88 | [-0.91, -0.84] | -22.35 | 148 | < .001 |    Tetrachoric |   150
Species.versicolor |  Species.virginica | -0.88 | [-0.91, -0.84] | -22.35 | 148 | < .001 |    Tetrachoric |   150
>

相关分析示例：

> library(correlation)
> 
> data <- simulate_simpson(n=100, groups=10)
> 
> 
> 
> library(ggplot2)
> 
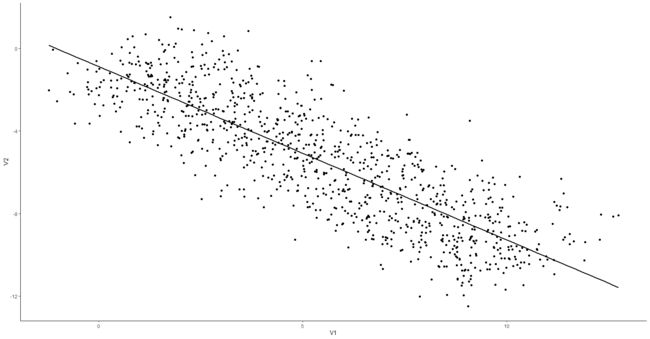
> ggplot(data, aes(x=V1, y=V2)) + 
+   geom_point() +
+   geom_smooth(colour="black", method="lm", se=FALSE) +
+   theme_classic()
`geom_smooth()` using formula 'y ~ x'
> 
> 
> correlation(data)
Parameter1 | Parameter2 |     r |         95% CI |      t |  df |      p |  Method | n_Obs
------------------------------------------------------------------------------------------
V1         |         V2 | -0.84 | [-0.86, -0.82] | -48.77 | 998 | < .001 | Pearson |  1000
>
R语言之可视化（31）扫地僧easystats（2）相关性分析_第2张图片

发现数据总的趋势是负相关



library(ggplot2)

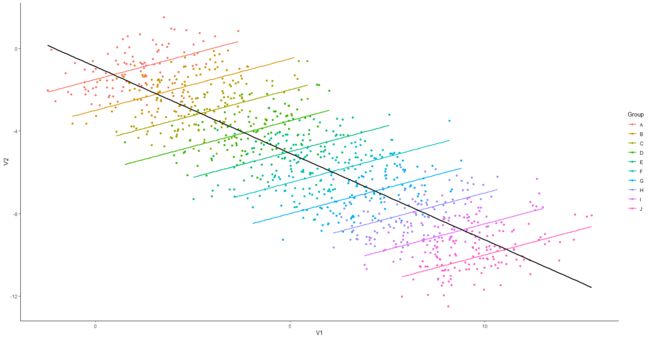
ggplot(data, aes(x=V1, y=V2)) + 
  geom_point(aes(colour=Group)) +
  geom_smooth(aes(colour=Group), method="lm", se=FALSE) + 
  geom_smooth(colour="black", method="lm", se=FALSE) + 
  theme_classic()
R语言之可视化（31）扫地僧easystats（2）相关性分析_第3张图片

但是分组后，发现组内是正相关

你可能感兴趣的:(R语言之可视化（31）扫地僧easystats（2）相关性分析)

  • vue项目报错取消页面红色遮罩（Uncaught runtime errors） 菜鸟许良个人笔记 vue.jsjavascript前端
    1.取消前2.vue.config.js里面添加overlay:falseconstpath=require("path");constresolve=(dir)=>{returnpath.join(__dirname,dir);};module.exports={publicPath:"./",transpileDependencies:[],chainWebpack:(config)=>{co
  • Python学习：Pandas库使用（二）之读写Excel文件——read_excel()和to_excel()函数及其参数详解 爬虫俗手小马达 python学习pandas
    在Python的Pandas库中，读取和写入Excel文件主要使用read_excel和to_excel函数。以下是详细用法和示例：1.读取Excel文件：pd.read_excel()importpandasaspd#读取Excel文件df=pd.read_excel('文件路径.xlsx',sheet_name='Sheet1',header=0,usecols='A:C',skiprows=
  • 怎么在wps里面进行批量序号替换通配符； Bruce-Lan wps
    删除所有的6.1.[1-9].[1-9].[1-9]的序号？6\.1\.[1-9]\.[1-9]\.[1-9]1，ctrl+f；2，点击替换，使用通配符；3，查找内容输入：6\.1\.[1-9]\.[1-9]\.[1-9]，替换内容自拟比如1.2.3.5.64，执行替换，搞定。
  • 2025 年成为 AI 独立开发者的 3 个步骤 程序员陆通 人工智能
    2025年成为AI独立开发者的3个步骤每天拆解一个AI应用或模型功能选择一个热门的AI应用或开源模型（如ChatGPT、MidJourney、Whisper），深度体验其核心功能，分析背后的技术实现。用笔记工具记录其亮点、缺点，以及你认为可以改进的地方。思考如何通过自己的开发能力优化这些功能，形成自己的产品思路。每天学习1小时AI开发相关技能针对独立开发者需要的核心技能，每天学习一点点，比如：如何
  • word中目录右边页码对不齐解决方法 Bruce-Lan office其他
    这个目录对不齐原因未知；解决方法：1，在视图中打开标尺；2，选择对不齐的目录项；如果整个目录都有出现不对齐，选择整个目录。3，拖动标尺，进行对齐；4，被治愈了。
  • 人工智能之数学基础：一个小例子帮你快速搞懂极大线性无关向量组 每天五分钟玩转人工智能 机器学习深度学习之数学基础人工智能线性代数机器学习极大线性无关向量组深度学习神经网络
    本文重点在上一节课程中，我们学习了线性相关和线性无关。当线性相关的时候，那么说明这组向量至少存在一个向量可以被其它向量给表示，可以被表示就说明这个向量就是可有可无的，可以被替代的，这里就涉及到极大线性无关向量组的概念了，本文对此进行学习。极大无关向量组的定义与性质定义在线性空间中，如果存在一个向量组，它满足以下两个条件：一是它本身是线性无关的；二是向量空间中的任何包含它的向量组，如果仍然保持线性无
  • PyInstaller 打包 exe 文件 cliffordl python综合python开发语言
    PyInstaller是一个第三方库，它能够在Windows、Linux、MacOSX等操作系统下将Python源文件打包。通过对源文件打包，Python程序可以在没有安装Python的环境中运行，也可以作为一个独立文件方便传递和管理。PyInstaller支持Python2.7和Python3.3+。可以在Windows、MacOSX和Linux上使用，但是并不是跨平台的，而是说你要是希望打包成
  • 求两个字符串的最长公共子序列 未来的JAVA高级开发工程师 算法Java算法动态规划
    packagecom.cjh.dp;publicclassdp3{publicstaticvoidmain(String[]args){//求两个字符串的最长公共子序列intl=method("abcxyz","abxyz");System.out.println(l);}privatestaticintmethod(Stringstring1,Stringstring2){//TODOAuto-
  • 强大的骚操作，9种不同的方法帮助你提高国内访问Github的速度 程序员大伟 Java学习javagithublinuxgitsvn
    1.GitHub镜像访问这里提供两个最常用的镜像地址：https://github.com.cnpmjs.orghttps://hub.fastgit.org也就是说上面的镜像就是一个克隆版的Github，你可以访问上面的镜像网站，网站的内容跟Github是完整同步的镜像，然后在这个网站里面进行下载克隆等操作。2.GitHub文件加速利用CloudflareWorkers对githubreleas
  • Pytorch: torch.diag()创建对角线张量 湫兮之风 pytorchpytorch人工智能python
    torch.diag()torch.diag是PyTorch中的一个函数，用于从给定的矩阵中提取对角线元素，或者构造一个以给定对角线元素为值的对角矩阵。这个函数对于矩阵分解和转换等操作非常重要。如果输入是一个向量（1D张量），torch.diag会返回一个以该向量为对角线元素的2D方阵。如果输入是一个矩阵（2D张量），则返回一个包含输入矩阵对角线元素的1D张量。torch.diag还允许你指定对角
  • C++：inline函数的作用 湫兮之风 c++c++算法开发语言
    1.基本概念inline是C++中的一个关键字，用于建议编译器将函数的调用替换为函数体本身，而不是执行传统的函数调用操作。函数调用通常涉及将参数压栈、跳转到函数代码处执行、返回结果等操作，对于一些小的、频繁调用的函数，这些开销可能会影响性能。使用inline可以避免这些开销。2.示例代码#include//定义一个inline函数inlineintadd(inta,intb){returna+b;
  • SpringCloud系列——5Spring Cloud 源码分析之OpenFeign 木木_2024 SpringCloud系列springcloudjavaspring架构
    学习目标为什么加一个注解就能实现远程过程调用呢？推导它底层的实现主流程？OpenFeign怎么实现RPC的基本功能的通过源码验证第1章OpenFeign主流程推导要明确OpenFeign的主流程首先我们还是要明确它的核心目标是什么？说白了，OpenFeign最核心的目标就是让客户端在远程调用过程中不需要做什么多余的操作，只要拿到一个对象，然后调用该对象的方法就好了，剩下的操作都交给OpenFeig
  • python连接elasticsearch实战（附完整代码） 当初 pythonelasticsearch
    python连接elasticsearchfromelasticsearchimportElasticsearchfromelasticsearch.helpersimportscanES_HOSTS=[{'host':'','port':9200,'scheme':'http'}]es=Elasticsearch(hosts=ES_HOSTS,basic_auth=('账号','密码'))#检查
  • Ruby语言详解 编程小郭 ruby开发语言后端
    Ruby语言详解Ruby，作为一种简单快捷的面向对象脚本语言，自20世纪90年代由日本人松本行弘（YukihiroMatsumoto）开发以来，便以其独特的魅力和强大的功能赢得了全球开发者的青睐。Ruby不仅继承了Perl、Smalltalk、Eiffel、Ada以及Lisp等多种语言的优点，还发展出了自己的特色和风格。一、Ruby语言的特点面向对象：Ruby从一开始就被设计成纯粹的面向对象语言，
  • 项目进度管理：如何使用甘特图实现精准跟踪？
    一、甘特图——项目进度管理的得力助手（一）甘特图的基本概念与构成甘特图（GanttChart）又称横道图、条状图，出现于20世纪初，是一种常用于项目管理的、按照时间进度标出工作活动的图表，以提出者亨利・L・甘特（HenrryL.Ganntt）先生的名字命名。它是一个二维平面图，用横轴表示项目进度或活动时间，比如可以按日期为单位，展示项目的整体时间范围，像从项目启动到结束所涵盖的天数、周数、月数等；
  • 2025年敏捷项目管理10大爆炸性趋势，前所未见！
    在当今快速发展的商业环境中，项目管理的重要性愈发凸显。敏捷项目管理作为一种灵活高效的管理方法，正逐渐成为众多企业的首选。随着技术的不断进步和市场需求的变化，我们对2025年敏捷项目管理的趋势充满期待。一、敏捷项目管理简介一方面，敏捷项目管理能够快速响应市场需求，实现高效交付。在竞争激烈的市场中，企业需要能够迅速调整项目方向，以满足客户不断变化的需求。敏捷方法论，如Scrum和Kanban等框架，以
  • R语言的面向对象编程 2501_90183952 包罗万象golang开发语言后端
    R语言的面向对象编程在现代编程中，面向对象编程（Object-OrientedProgramming，OOP）是一种重要的编程范式，它通过将数据和操作数据的函数结合在一起，来提高代码的重用性和可维护性。在R语言中，面向对象编程并不是一开始就被引入的，但随着其发展，R逐渐支持了多种面向对象编程的系统，例如S3、S4以及R6等。本文将深入探讨R语言的面向对象编程，介绍其基本概念、特点以及在实际应用中的
  • 2024金三银四必备：Java后端开发面试总结【25个技术专题】 2401_89790869 java面试开发语言
    16、List和Map、Set的区别？17、数组和链表分别比较适合用于什么场景，为什么？18、说说ConcurrentHashMap19、Java中ArrayList和LinkedList区别？20、TreeMap（可排序）21、请用两个队列模拟堆栈结构？22、Map中的key和value可以为null？23、数据结构基础之双向链表24、HashMap的底层实现25、ConcurrentHashM
  • HTML期末学生大作业-最新QQ音乐、网易云音乐、酷狗音乐、虾米音乐、咪咕音乐网站html+css+javascript 2401_89790869 html课程设计css
    href=“https://y.qq.com/n/ryqq/playlist/7772849553”>好评999+英文歌！轻松解压100％播放量：2.8亿扎心情歌丨爱到最后终是空欢喜播放量：510.4万如果词不达意就把爱藏心里播放量：1645.7万深情片段：深夜我还是会想起你播放量：2663.8万href=“https://y.qq.com/n/ryqq/playlist/7537828
  • 如何建设和维护数据仓库：深入指南 数据库数据库开发
    摘要数据仓库是企业数据管理的核心，它不仅支持决策制定，还能提供深入的数据分析。本文将详细介绍如何从零开始建设和维护一个高效、可靠的数据仓库，涵盖设计、实施、监控和优化的全过程。通过具体的代码示例和最佳实践，帮助读者深入理解数据仓库的构建和管理。引言数据仓库是企业数据管理的心脏，它集中存储和管理来自不同来源的数据，支持复杂的查询和分析。随着数据量的爆炸性增长，如何高效地建设和维护数据仓库成为企业面临
  • redis哨兵手动切换主节点 数据库
    说明由于线上redisMaster异常关机之后，重启redis哨兵模式三个节点都是slave，无法选择出主，一半都是固定在一台主节点上面执行操作如下手动进行master-slave切换登录192.168.1.11（master）主机的redis，执行shutdown命令关闭redis登录192.168.1.12（newmaster），执行如下命令：127.0.0.1:6379>slaveofnoo
  • Nginx进阶篇之端口转发 程序员
    nginx透传udp、tcp端口需要nginx编译时，支持加载stream模块。./configure--prefix=/usr/local/nginx--with-stream配置stream需要在nginx的http和events区域块之间配置即可。userroot;worker_processesauto;error_loglogs/error.log;pidsbin/nginx.pid;e
  • web前端常见的面试题总结 2401_84436095 程序员前端
    script.src=url+‘?’+data+‘callback=’+funcNamedocument.body.appendChild(script);//这里得到请求的数据，在回调函数中执行处理window[funcName]=function(data){callback(data)}}//使用jsonp(‘http:127.0.0.1:3000/api’,{},function(res)
  • OpenHarmony教程指南-自定义通知推送 码牛程序猿 鸿蒙工程师HarmonyOS鸿蒙harmonyos鸿蒙开发华为OpenHarmony鸿蒙工程师鸿蒙应用开发
    介绍本示例主要展示了通知过滤回调管理的功能，使用@ohos.notificationManager接口，进行通知监听回调，决定应用通知是否发送。效果预览使用说明1.在使用本应用时，需安装自定义通知角标应用；2.在主界面，进行通知过滤的开启及关闭；3.开启通知过滤后，可以选择允许通知的类型，去勾选后，相应类型的通知将不会发送出现通知栏；4.打开自定义通知角标应用应用，进行通知的发送，查看是否发送成功
  • 小白WEB前端学习（五） Sun ᥫᩣ涵 WEB前端前端学习
    续：小白WEB前端学习（四）继续正式学习CSS（三）6.float布局！主要用于左右做图片，右文字的题目标准流标准流也叫文档流，指的是标签在页面中默认的排布规则，使⼀个元素脱离标准文档流有三种方式1.浮动2.绝对定位3.固定定位例如:块元素独占一行，行内元素可以一行显示多个。浮动作用：让块元素水平排列属性名：float属性值：left和right浮动后会脱离标准流，等于开了一个新的页面，内容在的话
  • 寒假集训1.21 学长学姐我该怎么办 算法
    问题A:TYVJ1025单数？双数？内存限制：128MB时间限制：0.000S评测方式：文本比较命题人：外部导入提交：521解决：230返回比赛提交提交记录侧边提交题目描述Bessie那惨无人道的二年级老师搞了一个有N(1=n/2:print(key)问题N:寻找第K大的数内存限制：20MB时间限制：1.000S评测方式：文本比较命题人：liuyong提交：4033解决：1744返回比赛提交提交记
  • 用JavaScript实现找不同小游戏 算是难了 javascript开发语言前端websocket
    目录倒计时的实现找不同实现对canvas的初始化实现画布的分割,父盒子>子盒子>canvas找不同逻辑的判断实现图片的导入DOM节点的监听声明两个需要监听的节点禁用页面点击事件的函数DOM监听实现勋章分数增加和生命的减少减命逻辑死亡响应websocket交互定义给后端发送的数据包断线重连最后,调用封装好的websocket创建初始之物，其行必丑代码写的非常繁琐,有很多细节在复盘的时候也会想不起来为
  • python中常用排序操作——sort方法和sorted函数的使用，超详细，内置模板代码！！! 盲敲代码的阿豪 python实用知识点pythonsortedsort排序
    文章目录前言1、sort()方法的使用1.1基础操作1.2操作进阶（自定义排序的对象）2、sorted()函数的使用2.1基础操作2.2操作进行（自定义排序的对象）3、扩展：排序案例模板代码前言在Python中，排序的方法有多种，其中最常用的是使用内置的sort()方法和sorted()函数，接下来我将通过各种案例带领大家轻松学会这两种方法，同时还会扩展一些实用的排序案例模板代码。1、sort()
  • C++: Dtrees:load(constg String& filepath, const String& nodeName)中nodeName参数含义 湫兮之风 c++c++开发语言算法
    1.nodeName的作用当你保存模型时，整个决策树会被序列化到一个XML或YAML文件中。nodeName是加载时指定的一个逻辑路径，用于从文件中找到某个节点或子结构，而不是存储在文件中的字段。如果你不指定nodeName，OpenCV默认会尝试加载文件中根节点对应的模型。2.默认的行为如果你不指定nodeName，通常会加载文件的根节点：Ptrtree=cv::ml::DTrees::load
  • 2025年使用 npx + expo + react native 创建一个项目 expoyarnreact
    为什么要用expo？因为reactnative官方推荐的为什么要用npx？因为expo官方推荐的怎么用呢？看expo的官方文档：https://docs.expo.dev/npxcreate-expo-app@latest这里需要注意，如果你问chatgpt，会得到npminstall-gexpo-cli来安装,但是这样方式已经过期了，不要再用了─➤expoversionWARNING:Thele
  • redis学习笔记——不仅仅是存取数据 Everyday都不同 returnSourceexpire/delincr/lpush数据库分区redis
    最近项目中用到比较多redis，感觉之前对它一直局限于get/set数据的层面。其实作为一个强大的NoSql数据库产品，如果好好利用它，会带来很多意想不到的效果。（因为我搞java，所以就从jedis的角度来补充一点东西吧。PS：不一定全，只是个人理解，不喜勿喷）   1、关于JedisPool.returnSource(Jedis jeids)   这个方法是从red
  • SQL性能优化-持续更新中。。。。。。 atongyeye oraclesql
    1 通过ROWID访问表--索引 你可以采用基于ROWID的访问方式情况,提高访问表的效率, , ROWID包含了表中记录的物理位置信息..ORACLE采用索引(INDEX)实现了数据和存放数据的物理位置(ROWID)之间的联系. 通常索引提供了快速访问ROWID的方法,因此那些基于索引列的查询就可以得到性能上的提高. 2 共享SQL语句--相同的sql放入缓存 3 选择最有效率的表
  • [JAVA语言]JAVA虚拟机对底层硬件的操控还不完善 comsci JAVA虚拟机
         如果我们用汇编语言编写一个直接读写CPU寄存器的代码段，然后利用这个代码段去控制被操作系统屏蔽的硬件资源，这对于JVM虚拟机显然是不合法的，对操作系统来讲，这样也是不合法的，但是如果是一个工程项目的确需要这样做，合同已经签了，我们又不能够这样做，怎么办呢？ 那么一个精通汇编语言的那种X客，是否在这个时候就会发生某种至关重要的作用呢？ &n
  • lvs- real 男人50 LVS
    #!/bin/bash # # Script to start LVS DR real server. # description: LVS DR real server # #.  /etc/rc.d/init.d/functions VIP=10.10.6.252 host='/bin/hostname' case "$1" in sta
  • 生成公钥和私钥 oloz DSA安全加密
    package com.msserver.core.util; import java.security.KeyPair; import java.security.PrivateKey; import java.security.PublicKey; import java.security.SecureRandom; public class SecurityUtil {
  • UIView 中加入的cocos2d，背景透明 374016526 cocos2dglClearColor
    要点是首先pixelFormat:kEAGLColorFormatRGBA8，必须有alpha层才能透明。然后view设置为透明glView.opaque = NO;[director setOpenGLView:glView];[self.viewController.view setBackgroundColor:[UIColor clearColor]];[self.viewControll
  • mysql常用命令 香水浓 mysql
    连接数据库 mysql -u troy -ptroy 备份表 mysqldump -u troy -ptroy mm_database mm_user_tbl > user.sql 恢复表（与恢复数据库命令相同） mysql -u troy -ptroy mm_database < user.sql 备份数据库 mysqldump -u troy -ptroy
  • 我的架构经验系列文章 - 后端架构 - 系统层面 agevs JavaScriptjquerycsshtml5
    系统层面： 高可用性 所谓高可用性也就是通过避免单独故障加上快速故障转移实现一旦某台物理服务器出现故障能实现故障快速恢复。一般来说，可以采用两种方式，如果可以做业务可以做负载均衡则通过负载均衡实现集群，然后针对每一台服务器进行监控，一旦发生故障则从集群中移除；如果业务只能有单点入口那么可以通过实现Standby机加上虚拟IP机制，实现Active机在出现故障之后虚拟IP转移到Standby的快速
  • 利用ant进行远程tomcat部署 aijuans tomcat
    在javaEE项目中，需要将工程部署到远程服务器上，如果部署的频率比较高，手动部署的方式就比较麻烦，可以利用Ant工具实现快捷的部署。这篇博文详细介绍了ant配置的步骤（http://www.cnblogs.com/GloriousOnion/archive/2012/12/18/2822817.html），但是在tomcat7以上不适用，需要修改配置，具体如下： 1.配置tomcat的用户角色
  • 获取复利总收入 baalwolf 获取
           public static void main(String args[]){         int money=200;         int year=1;         double rate=0.1; &
  • eclipse.ini解释 BigBird2012 eclipse
    大多数java开发者使用的都是eclipse，今天感兴趣去eclipse官网搜了一下eclipse.ini的配置，供大家参考，我会把关键的部分给大家用中文解释一下。还是推荐有问题不会直接搜谷歌，看官方文档，这样我们会知道问题的真面目是什么，对问题也有一个全面清晰的认识。 Overview 1、Eclipse.ini的作用 Eclipse startup is controlled by th
  • AngularJS实现分页功能 bijian1013 JavaScriptAngularJS分页
            对于大多数web应用来说显示项目列表是一种很常见的任务。通常情况下，我们的数据会比较多，无法很好地显示在单个页面中。在这种情况下，我们需要把数据以页的方式来展示，同时带有转到上一页和下一页的功能。既然在整个应用中这是一种很常见的需求，那么把这一功能抽象成一个通用的、可复用的分页（Paginator）服务是很有意义的。   &nbs
  • [Maven学习笔记三]Maven archetype bit1129 ArcheType
    archetype的英文意思是原型，Maven archetype表示创建Maven模块的模版，比如创建web项目，创建Spring项目等等.   mvn archetype提供了一种命令行交互式创建Maven项目或者模块的方式，   mvn archetype   1.在LearnMaven-ch03目录下，执行命令mvn archetype:gener
  • 【Java命令三】jps bit1129 Java命令
    jps很简单，用于显示当前运行的Java进程，也可以连接到远程服务器去查看   [hadoop@hadoop bin]$ jps -help usage: jps [-help] jps [-q] [-mlvV] [<hostid>] Definitions: <hostid>: <hostname>[:
  • ZABBIX2.2 2.4 等各版本之间的兼容性 ronin47
    zabbix更新很快，从2009年到现在已经更新多个版本，为了使用更多zabbix的新特性，随之而来的便是升级版本，zabbix版本兼容性是必须优先考虑的一点 客户端AGENT兼容 zabbix1.x到zabbix2.x的所有agent都兼容zabbix server2.4：如果你升级zabbix server，客户端是可以不做任何改变，除非你想使用agent的一些新特性。 Zabbix代理（p
  • unity 3d还是cocos2dx哪个适合游戏？ brotherlamp unity自学unity教程unity视频unity资料unity
    unity 3d还是cocos2dx哪个适合游戏？ 问：unity 3d还是cocos2dx哪个适合游戏？ 答：首先目前来看unity视频教程因为是3d引擎，目前对2d支持并不完善，unity 3d 目前做2d普遍两种思路，一种是正交相机，3d画面2d视角，另一种是通过一些插件，动态创建mesh来绘制图形单元目前用的较多的是2d toolkit，ex2d，smooth moves，sm2，
  • 百度笔试题：一个已经排序好的很大的数组，现在给它划分成m段，每段长度不定，段长最长为k，然后段内打乱顺序，请设计一个算法对其进行重新排序 bylijinnan java算法面试百度招聘
    import java.util.Arrays; /** * 最早是在陈利人老师的微博看到这道题： * #面试题#An array with n elements which is K most sorted，就是每个element的初始位置和它最终的排序后的位置的距离不超过常数K * 设计一个排序算法。It should be faster than O(n*lgn)。
  • 获取checkbox复选框的值 chiangfai checkbox
    <title>CheckBox</title> <script type = "text/javascript"> doGetVal: function doGetVal() { //var fruitName = document.getElementById("apple").value;//根据
  • MySQLdb用户指南 chenchao051 mysqldb
    原网页被墙，放这里备用。 MySQLdb User's Guide Contents Introduction Installation _mysql MySQL C API translation MySQL C API function mapping Some _mysql examples MySQLdb
  • HIVE 窗口及分析函数 daizj hive窗口函数分析函数
    窗口函数应用场景： （1）用于分区排序 （2）动态Group By （3）Top N （4）累计计算 （5）层次查询 一、分析函数 用于等级、百分点、n分片等。 函数             说明 RANK()     &nbs
  • PHP ZipArchive 实现压缩解压Zip文件 dcj3sjt126com PHPzip
    PHP ZipArchive 是PHP自带的扩展类，可以轻松实现ZIP文件的压缩和解压，使用前首先要确保PHP ZIP 扩展已经开启，具体开启方法就不说了，不同的平台开启PHP扩增的方法网上都有，如有疑问欢迎交流。这里整理一下常用的示例供参考。 一、解压缩zip文件 01 02 03 04 05 06 07 08 09 10 11
  • 精彩英语贺词 dcj3sjt126com 英语
    I'm always here              我会一直在这里支持你                &nb
  • 基于Java注解的Spring的IoC功能 e200702084 javaspringbeanIOCOffice
                                      
  • java模拟post请求 geeksun java
    一般API接收客户端（比如网页、APP或其他应用服务）的请求，但在测试时需要模拟来自外界的请求，经探索，使用HttpComponentshttpClient可模拟Post提交请求。 此处用HttpComponents的httpclient来完成使命。 import org.apache.http.HttpEntity ; import org.apache.http.HttpRespon
  • Swift语法之 ---- ?和!区别 hongtoushizi ?swift!
    转载自： http://blog.sina.com.cn/s/blog_71715bf80102ux3v.html   Swift语言使用var定义变量，但和别的语言不同，Swift里不会自动给变量赋初始值，也就是说变量不会有默认值，所以要求使用变量之前必须要对其初始化。如果在使用变量之前不进行初始化就会报错： var stringValue : String //
  • centos7安装jdk1.7 jisonami jdkcentos
    安装JDK1.7 步骤1、解压tar包在当前目录 [root@localhost usr]#tar -xzvf jdk-7u75-linux-x64.tar.gz 步骤2：配置环境变量 在etc/profile文件下添加 export JAVA_HOME=/usr/java/jdk1.7.0_75 export CLASSPATH=/usr/java/jdk1.7.0_75/lib
  • 数据源架构模式之数据映射器 home198979 PHP架构数据映射器datamapper
    前面分别介绍了数据源架构模式之表数据入口、数据源架构模式之行和数据入口数据源架构模式之活动记录，相较于这三种数据源架构模式，数据映射器显得更加“高大上”。   一、概念 数据映射器（Data Mapper）：在保持对象和数据库（以及映射器本身）彼此独立的情况下，在二者之间移动数据的一个映射器层。概念永远都是抽象的，简单的说，数据映射器就是一个负责将数据映射到对象的类数据。 &nb
  • 在Python中使用MYSQL pda158 mysqlpython
    缘由 　　近期在折腾一个小东西须要抓取网上的页面。然后进行解析。将结果放到 数据库中。 　　了解到 Python在这方面有优势，便选用之。 　　由于我有台 server上面安装有 mysql，自然使用之。在进行数据库的这个操作过程中遇到了不少问题，这里 记录一下，大家共勉。 　　 python中mysql的调用 　　 百度之后能够通过MySQLdb进行数据库操作。
  • 单例模式 hxl1988_0311 java单例设计模式单件
    package com.sosop.designpattern.singleton; /* * 单件模式：保证一个类必须只有一个实例，并提供全局的访问点 * * 所以单例模式必须有私有的构造器，没有私有构造器根本不用谈单件 * * 必须考虑到并发情况下创建了多个实例对象 * */ /** * 虽然有锁，但是只在第一次创建对象的时候加锁，并发时不会存在效率
  • 27种迹象显示你应该辞掉程序员的工作 vipshichg 工作
    1、你仍然在等待老板在2010年答应的要提拔你的暗示。 2、你的上级近10年没有开发过任何代码。 3、老板假装懂你说的这些技术，但实际上他完全不知道你在说什么。 4、你干完的项目6个月后才部署到现场服务器上。 5、时不时的，老板在检查你刚刚完成的工作时，要求按新想法重新开发。 6、而最终这个软件只有12个用户。 7、时间全浪费在办公室政治中，而不是用在开发好的软件上。 8、部署前5分钟才开始测试。
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他