九、数字图像处理之图像复原(2)
数字图像处理之图像复原(2)
- (七)约束的最小二乘法(规则化)滤波
- (八)利用露西-查理德森算法的迭代非线性复原
- (九)盲去卷积
- (十)来自投影的图像重建
-
- (1)函数radon
- (2)函数iradon
- (3)扇形射束的数据处理
(七)约束的最小二乘法(规则化)滤波
说明:另一个容易接受的线性复原方法叫约束的最小二乘法滤波,也称为规则化滤波。两个函数f和h的2D离散卷积数学表达式如下所示:
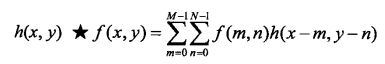
在matlab中是用函数deconvreg实现的,基本语法为:
frest = deconvreg(g,PSF,NOISEPOWER,RANGE); %g是被污染的图像,frest是复原的图像
如果没有NOISEPOWER和RANGE这两个参数,则会产生逆滤波效果。
实验代码及结果如下所示:
f = imread('C:\Users\Public\Pictures\Sample Pictures\horse.jpg');
f1 = im2double(rgb2gray(f));
g = imnoise(f,'poisson');
PSF = fspecial('motion',4,45);
frest1 = deconvreg(g,PSF,4); %NOISEPOWER的初试估计为4
frest2 = deconvreg(g,PSF,0.4,[1e-7 1e7]);
subplot(121),imshow(frest1,[]),title('参数为4的滤波');
subplot(122),imshow(frest2,[]),title('参数为0.4、范围为[1e-7 1e7]的滤波');
PSF = fspecial('motion',4,45);
PSF = fspecial('motion',2,45);
(图三)

(图四)
 对比上面四幅图,没有看出同一幅图的两幅图有什么差别。通过修改deconvreg的参数噪声能力和范围之后,得到如下结果:
对比上面四幅图,没有看出同一幅图的两幅图有什么差别。通过修改deconvreg的参数噪声能力和范围之后,得到如下结果:
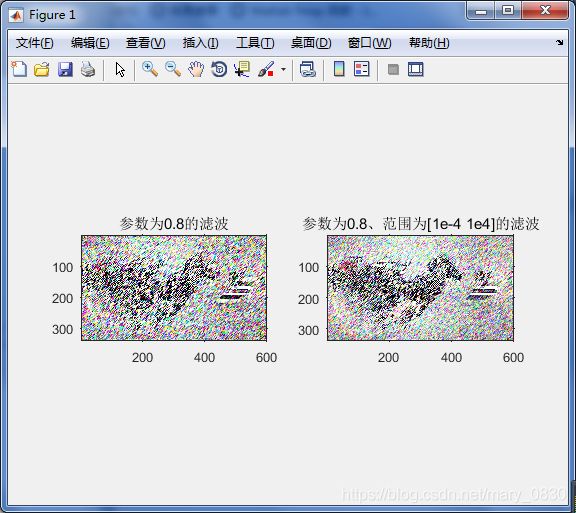
frest1 = deconvreg(g,PSF,0.8); %NOISEPOWER的初试估计为0.8
frest2 = deconvreg(g,PSF,0.8,[1e-4 1e4]);
结论:
通过修改参数可以使得约束最小二乘法的滤波效果变好;更换图像后,滤波效果也是很明显,图像并没有出现模糊,但还是出现了噪声。调整参数后,虽然滤波结果仍存在很多不足,但至少基本可以看出细节及内容。修改参数后得到的图五,有范围的约束最小二乘法滤波的图像显示,图像没有那么模糊,马匹后面的部门没有虚化和晕染,比前面没有范围的图像清晰一些,但是还是存在噪声很严重。应该是RANGE限制了图像的噪声范围,使得噪声的随机性降低,固定于一个范围内,因此显现的图像会比无范围的更加好一些。
注意: 若复原图像呈现运算中由离散傅里叶变换引入的振铃,在通常情况下,在调用函数deconvreg之前,需要使用函数edgetaper来帮助。
(八)利用露西-查理德森算法的迭代非线性复原
说明:这种算法是一种非线性算法,简称为L-R算法。L-R算法起源于最大似然公司,在这个方程式中,图像是用泊松统计建模的。数学表达式如下:
L-R算法用deconvlucy函数实现,基本语法是:
f = deconvlucy(g,PSF,NUMIT,DAMPAR,WEIGHT); %f是复原图像,g是退化图像,PSF是点扩散函数,NUMIT是迭代次数(默认为10)
其中,DAMPAR是标量,指定了结果图像与原始图像g之间的偏离阈值。当像素值偏离原值的范围在DAMPAR内时,就不用再迭代。这既抑制了图像像素噪声,又保留图像细节。默认值为0(无衰减)。WEIGHT是数组,大小与g相同,它为每个像素都施以权重以反映像素的质量。
注意: 若复原图像呈现运算中由离散傅里叶变换引入的振铃,在通常情况下,在调用函数deconvlucy之前,需要使用函数edgetaper来帮助。
实验代码:
g = checkerboard(8); %产生一幅64×64的方形图像
subplot(131),imshow(pixeldup(g,8)),title('原始图像'); %用函数pixeldup将图像大小放大为512×512像素
PSF = fspecial('gaussian',7,10); %产生7×7大小、标准差为10的高斯PSF
SD = 0.01;
g = imnoise(imfilter(g,PSF),'gaussian',0,SD^2); %添加高斯噪声
subplot(132),imshow(g,[]),title('高斯噪声污染模糊后的图像');
DAMPAR = 10*SD; %对参数DAMPAR赋10倍于SD的值
LIM = ceil(size(PSF,1)/2); %设置参数WEIGHT
WEIGHT = zeros(size(g)); %大小为64×64,值为0的4像素宽的边界
WEIGHT(LIM + 1:end - LIM,LIM + 1:end - LIM) = 1; %其他像素为1
NUMIT = 5;
f5 =deconvlucy(g,PSF,NUMIT,DAMPAR,WEIGHT);
subplot(133),imshow(pixeldup(f5,8),[]),title('用参数为5的迭代复原图像');
实验结果:
NUMIT = 10;
f10 =deconvlucy(g,PSF,NUMIT,DAMPAR,WEIGHT);
subplot(131),imshow(pixeldup(f10,8),[]),title('用参数为10的迭代复原图像');
NUMIT = 25;
f25 =deconvlucy(g,PSF,NUMIT,DAMPAR,WEIGHT);
subplot(132),imshow(pixeldup(f25,8),[]),title('用参数为25的迭代复原图像');
NUMIT = 200;
f200 =deconvlucy(g,PSF,NUMIT,DAMPAR,WEIGHT);
subplot(133),imshow(pixeldup(f200,8),[]),title('用参数为200的迭代复原图像');
结论: 即使增加了迭代次数,但在复原结果方面并没有明显的改善。只能对比出迭代次数越多,得到的图像比之前亮一些。非线性迭代法滤波并没有很好的滤波效果,还是使得滤波图像更加棋盘化,这样的效果是由于像素灰度级不够而引起的。也说明了露西-查理德森算法的迭代非线性复原没有很好的还原高斯噪声污染过的图像。
(九)盲去卷积
说明:盲去卷积是对随机噪声污染的量进行估计时采用的最佳策略。
在matlab中用函数deconvblind来执行盲去卷积,基本语法如下:
[fr,PSF] = deconvblind(g,INITPSF,NUMIT,DAMPAR,WEIGHT);
使用最大似然算法对图像g解卷积,返回去模糊图像fr和恢复的点扩散函数PSF。 生成的PSF是与INITPSF相同大小的正数组,归一化,所以它的总和增加到1。PSF的恢复受其初始猜测大小INITPSF的影响较大,而其值较小(一个数组是一个更安全的猜测)。为了改善恢复,可以传入附加参数,如NUMIT,DAMPAR,WEIGHT。
NUMIT(可选)是迭代次数(默认值为10)。DAMPAR(可选)是一个数组,用于指定图像g(根据泊松噪声的标准偏差)的结果图像的阈值偏差,低于此值会发生阻尼。 对于在DAMPAR值内偏离其原始值的像素,迭代被抑制。 这可以抑制这些像素中的噪音,并在其他地方保留必要的图像细节。 默认值为0(无阻尼)。WEIGHT(可选)分配给每个像素以反映相机的拍摄质量。 将一个坏像素分配给零权值,从而排除该像素。 您可以根据平场校正的数量来调整自己的体重,而不是给予好像素的权重。 默认值是与输入图像I大小相同的单位数组。
注意: 若复原图像呈现运算中由离散傅里叶变换引入的振铃,在通常情况下,在调用函数deconvblind之前,需要使用函数edgetaper来帮助。
实验代码:
g = checkerboard(8); %产生一幅64×64的方形图像
g = imnoise(imfilter(g,PSF),'gaussian',0,SD^2); %添加高斯噪声
PSF = fspecial('gaussian',7,10); %产生7×7大小、标准差为10的高斯PSF
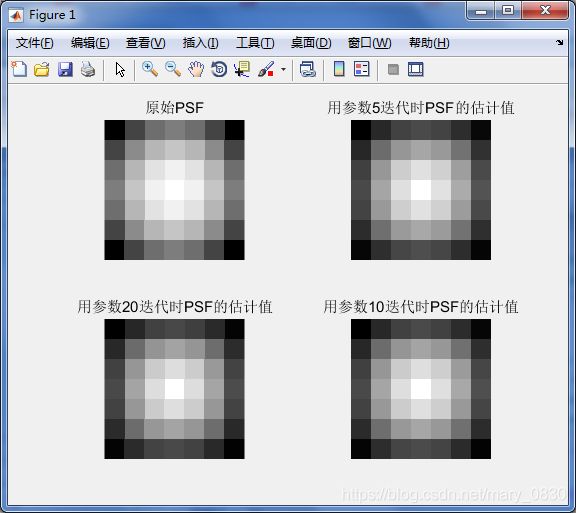
subplot(221),imshow(pixeldup(PSF,73),[]),title('原始PSF');
DAMPAR = 10*SD; %对参数DAMPAR赋10倍于SD的值
LIM = ceil(size(PSF,1)/2); %设置参数WEIGHT
WEIGHT = zeros(size(g)); %大小为64×64,值为0的4像素宽的边界
WEIGHT(LIM + 1:end - LIM,LIM + 1:end - LIM) = 1; %其他像素为1
SD = 0.01;
g = imnoise(imfilter(g,PSF),'gaussian',0,SD^2); %添加高斯噪声
INITPSF = ones(size(PSF));
NUMIT = 5;
[g5,PSF5] = deconvblind(g,INITPSF,NUMIT,DAMPAR,WEIGHT);
subplot(222),imshow(pixeldup(PSF5,73),[]),title('用参数5迭代时PSF的估计值');
NUMIT = 20;
[g20,PSF20] = deconvblind(g,INITPSF,NUMIT,DAMPAR,WEIGHT);
subplot(223),imshow(pixeldup(PSF20,73),[]),title('用参数20迭代时PSF的估计值');
NUMIT = 10;
[g10,PSF10] = deconvblind(g,INITPSF,NUMIT,DAMPAR,WEIGHT);
subplot(224),imshow(pixeldup(PSF10,73),[]),title('用参数10迭代时PSF的估计值');
实验结果:
 实验结论:
实验结论:
以上图只是改变了参数迭代的次数,其他的并没有修改。从修改后的看出,迭代次数为5的估计值图像的四个角颜色变深了,图像整体的颜色也变深了;迭代次数为10的虽然整体颜色也有点深,但是没有迭代次数是5那么严重,随着迭代次数的增加,正如参数为20的图像,在这几幅图中接近原图像。
(十)来自投影的图像重建
说明:一维投影的图像重建是医学中的重要应用之一。

当收集到一副图像各个角度的投影后,并希望通过这些投影的图像重建原图像。
(1)函数radon
函数radon是用来为给定的二维矩阵列产生一组平行射线投影,基本语法是:
R =radon(I,theta); %I是二维阵列,theta是角度值的一维阵列
更一般的语法是:
[R,xp] = radon(I,theta); %xp包含沿着x’轴的坐标值
用来产生众所周知的图像的某个有用函数语法为:
P = phantom(def,n); %def是指定产生头部模型类型的字符串,n是行数和列数(默认值为256)
其中,字符串def的可用值为:‘Shepp-Logan’(对比度很低)和’ModifiedShepp-Logan’(改进了对比度)。
实验代码:
f = imread('C:\Users\Public\Pictures\Sample Pictures\horse.jpg ');
g1=rgb2gray(f);
g1(100:500,250:350) = 1;
g2 = phantom('Modified Shepp-Logan',600);
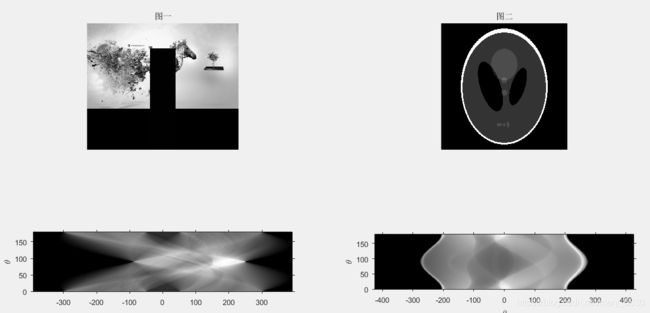
subplot(221),imshow(g1),title('图一');
subplot(222),imshow(g2),title('图二');
theta = 0:0.5:179.5;
[R1,xp1] = radon(g1,theta); %执行雷登变换
[R2,xp2] = radon(g2,theta);
R1 = flipud(R1'); %投影图像
R2 = flipud(R2');
subplot(223),imshow(R1,[],'XData',xp1([1 end]),'YData',[179.5 0]) %显示投影图像
axis xy
axis on
xlabel('\rho'),ylabel('\theta')
subplot(224),imshow(R2,[],'XData',xp2([1 end]),'YData',[179.5 0])
axis xy
axis on
xlabel('\rho'),ylabel('\theta')
(2)函数iradon
函数iradon从给定的取自不同角度的一组投影来重建一幅图像(切片)。简单说来,就是iradon计算反randon变换。基本语法是:
I = iradon(R,theta,interp,filter,frequency_scaling,output_size)
其中,
R是反投影数据,列是从左到右以角度渐增的函数来组织的一维反投影;
theta描述角度,据此来获取头像;
interp是字符串,定义了用于产生最终重建图像的内插方法;
filter指定了在滤波反投影计算中使用的滤波器;
frequency_scaling是处于(0,1)范围内的标量,通过改变频率轴的比例来修改滤波器,默认值为1。若frequency_scaling小于1,滤波器被压缩,以适应【0,frequency_scaling】范围;
output_size是标量,规定了重建图像的行列数,若没有指定,则由投影的长度来确定:output_size = 2*floor(size(R,1)/(2*sqrt(2)))
实验代码:
theta = 0:0.5:179.5;
R1 = radon(g1,theta);
R2 = radon(g2,theta);
f1 = iradon(R1,theta,'none');
f2 = iradon(R2,theta,'none');
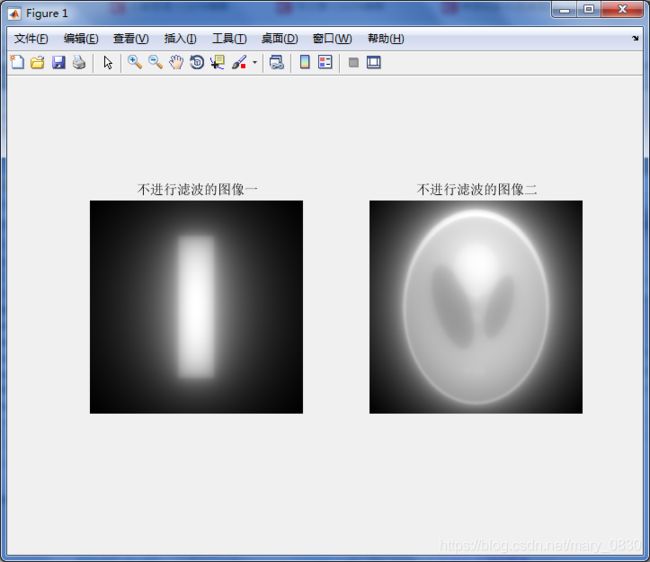
subplot(121),imshow(f1,[]),title('不进行滤波的图像一');
subplot(122),imshow(f2,[]),title('不进行滤波的图像二');
结论: 由图可知,不进行滤波的效果图最差,而且模糊了图像,只能看到一个大致的轮廓,基本看不到原来的细节(就像上图有马匹的图一样,只能大概看出有一匹马,其他细节完全无法识别)。
实验代码:
f1_ram = iradon(R1,theta); %默认值滤波
f2_ram = iradon(R2,theta);
subplot(121),imshow(f1_ram ,[]),title('默认滤波的图像一');
subplot(122),imshow(f2_ram ,[]),title('默认滤波的图像二');
f1_hamm = iradon(R1,theta,'Hamming'); %汉明窗滤波
f2_hamm = iradon(R2,theta,'Hamming');
subplot(121),imshow(f1_hamm ,[]),title('用汉明窗滤波的图像一');
subplot(122),imshow(f2_hamm ,[]),title('用汉明窗滤波的图像二');
实验代码:
f1_hann= iradon(R1,theta,'Hann'); %韩窗滤波
f2_hann = iradon(R2,theta,'Hann');
subplot(121),imshow(f1_hann,[]),title('用韩窗滤波的图像一');
subplot(122),imshow(f2_hann ,[]),title('用韩窗滤波的图像二');
结论: 默认值滤波器滤波后的效果比较差,汉明窗和韩窗的效果都基本还原了图像,但也是会模糊图像。图像二的三种滤波法看出,默认值滤波器滤波的效果差,不仅模糊图像而且降低对比度;图像一(图像是马匹)对比看出,默认值滤波器模糊图像。
实验代码:
f1_near = iradon(R1,theta,'nearest'); %最近邻内插法
f1_lin = iradon(R1,theta,'linear'); %线性内插法
f1_cub = iradon(R1,theta,'cubic'); %三次内插法
subplot(131),imshow(f1_near,[]),,title('用最近邻内插法滤波的图像一');
subplot(132),imshow(f1_lin,[]),,title('用线性内插滤波的图像一');
subplot(133),imshow(f1_cub,[]),,title('用三次内插滤波的图像一');
结论: 第一次用图显示不出三种内插法哪种比较好,之后用了马匹的图像,明显的看出线性内插和三次内插法比最近邻内插法滤波效果好。放大之后发现,最近邻内插法使得图像不仅模糊还产生噪声;线性内插法增加了对比度;三次内插发则细化了细节部分,对比更加明显。
(3)扇形射束的数据处理
给定扇形射束数据,工具箱使用的方法是把扇形射束变换为与之对应的平行射束,然后用早期的平行射束得到反投影。在扇形射束中,射线可以描述成一条直线L(ρ,θ)。平行射束和扇形射束存在某种对应关系:
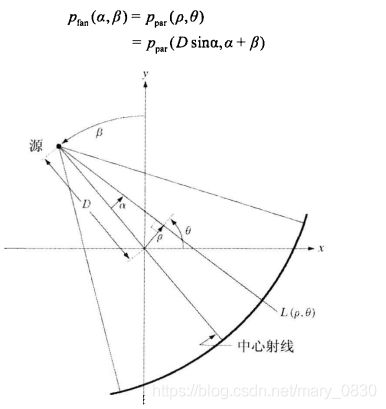
其中,![]() 是相应的平行射束投影。
是相应的平行射束投影。
matlab中用函数fanbeam产生扇形射束投影,基本语法为:
B = fanbeam(g,D,param),val1,param2,val2,...) %g是包含被投射物体的图像,D是从扇形射束的顶点到旋转中心的距离
假定旋转中心是图像的中心,规定D大于g的一半:
D = K*sqrt(size(g,1)^2 + size(g,2)^2)/2 %K是大于1的常数
函数fanbeam通过计算对于任何角度覆盖全部图像需要多少射线数来决定传感器的数目。
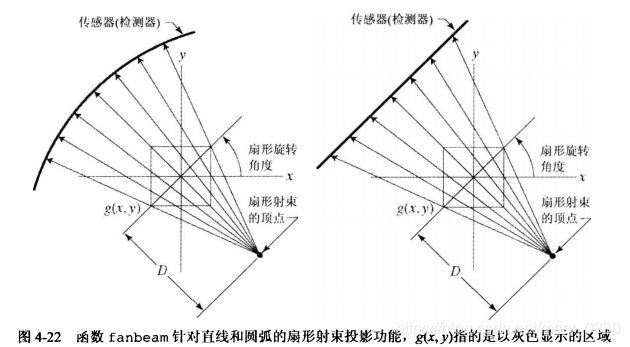
实验代码及效果如下:
g1 = zeros(600,600);
g1(100:500,250:350) = 1;
g2 = phantom('Modified Shepp-Logan',600);
D = 1.5*hypot(size(g1,1),size(g2,2))/2;
B1_line = fanbeam(g1,D,'FanSensorGeometry','line','FanSensorSpacing',1,'FanRotationIncrement',0.5);
B1_line = flipud(B1_line');
B2_line = fanbeam(g2,D,'FanSensorGeometry','line','FanSensorSpacing',1,'FanRotationIncrement',0.5);
B2_line = flipud(B2_line');
B1_arc = fanbeam(g1,D,'FanSensorGeometry','arc','FanSensorSpacing',0.08,'FanRotationIncrement',0.5);
B1_arc = flipud(B1_arc');
B2_arc = fanbeam(g2,D,'FanSensorGeometry','arc','FanSensorSpacing',0.08,'FanRotationIncrement',0.5);
B2_arc = flipud(B2_arc');
subplot(221),imshow(B1_line,[]),title('g1直线扇形射束图像');
subplot(222),imshow(B2_line,[]),title('g2直线扇形射束图像');
subplot(223),imshow(B1_arc,[]),title('g1圆弧扇形射束图像');
subplot(224),imshow(B2_arc,[]),title('g2圆弧扇形射束图像');
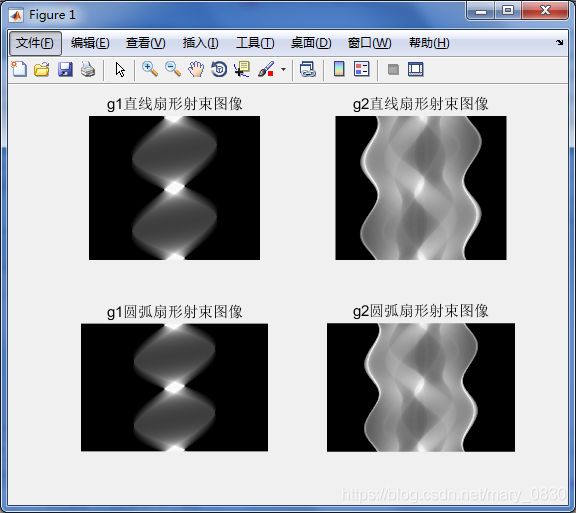
我们发现相应的外形十分不同,扇形射束投影出现了“歪斜”,这是扇形直接对于平行射束的结果。直线扇形射束图像比圆弧扇形射束更暗,这是与传感器的形状有关,圆弧扇形射束扫到检测的范围比较宽且呈现弧度,因此显示出的图像比较亮一些。
函数ifanbeam可用来给定一组扇形射束投影得到滤波反投影图像:
I = ifanbeam(B,D,...,param1,val1,param2,val2,..);
实验代码及效果如下:
g = phantom('Modified Shepp-Logan',600);
D = 1.5*hypot(size(g1,1),size(g2,2))/2;
B1 = fanbeam(g,D);
f1= ifanbeam(B1,D);
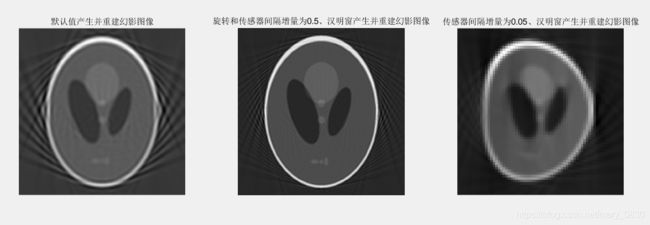
subplot(131),imshow(f1,[]),title('默认值产生并重建幻影图像');
B2 = fanbeam(g,D,'FanRotationIncrement',0.5,'FanSensorSpacing',0.5);
f2 = ifanbeam(B2,D,'FanRotationIncrement',0.5,'FanSensorSpacing',0.5,'Filter','Hamming');
subplot(132),imshow(f2,[]),title('旋转和传感器间隔增量为0.5、汉明窗产生并重建幻影图像');
B3 = fanbeam(g,D,'FanRotationIncrement',0.5,'FanSensorSpacing',0.5);
f3 = ifanbeam(B3,D,'FanRotationIncrement',0.5,'FanSensorSpacing',0.05,'Filter','Hamming');
subplot(133),imshow(f3,[]),title('传感器间隔增量为0.05、汉明窗产生并重建幻影图像');
扇形和平行投影间转换的函数:
P = fan2para(F,D,param1,val1,param2,val2,...) %扇形数据转换为平行射束数据
F = para2fan(P,D,param1,val1,param2,val2,...) %平行数据转换为扇形射束数据
实验代码及效果图:
g1 = phantom('Modified Shepp-Logan',600);
g1(100:500,250:350) = 1;
g2 = phantom('Modified Shepp-Logan',600);
D = 1.5*hypot(size(g1,1),size(g2,2))/2;
B1_line = fanbeam(g1,D,'FanSensorGeometry','line','FanSensorSpacing',1,'FanRotationIncrement',0.5);
B2_arc= fanbeam(g2,D,'FanSensorGeometry','arc','FanSensorSpacing',0.08,'FanRotationIncrement',0.5);
P1_line = fan2para(B1_line,D,'FanRotationIncrement',0.5,'FanSensorGeometry','line','FanSensorSpacing',1,'ParallelCoverage','halfcycle','ParallelRotationIncrement',0.5,'ParallelSensorSpacing',1);
P2_arc = fan2para(B2_line,D,'FanRotationIncrement',0.5,'FanSensorGeometry','arc','FanSensorSpacing',0.08,'ParallelCoverage','halfcycle','ParallelRotationIncrement',0.5,'ParallelSensorSpacing',1);
P1_line = flipud(P1_line');
P2_arc = flipud(P2_arc');
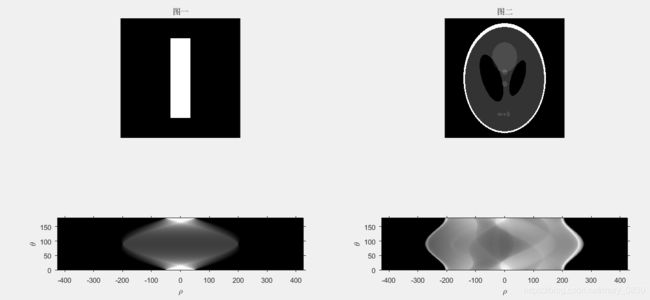
subplot(121),imshow(P1_line,[]),title('扇形射束投影');
subplot(122),imshow(P2_arc,[]),title('平行射束投影');