机器学习笔记（五）——最优化方法：梯度下降（BGD&SGD）

一、概念

（一） 为什么需要梯度下降算法

仅从数学抽象的角度来看：每个模型都有自己的损失函数，不管是监督式学习还是非监督式学习。损失函数包含了若干个位置的模型参数，比如在多元线性回归中，损失函数： $$(y-X_b\cdot \theta {)}^T(X_b\cdot \theta )$$ ，其中向量表示未知的模型参数，我们就是要找到使损失函数尽可能小的参数未知模型参数。

在学习简单线性回归时，我们使用最小二乘法来求损失函数的最小值，但是这只是一个特例。在绝大多数的情况下，损失函数是很复杂的（比如逻辑回归），根本无法得到参数估计值的表达式。因此需要一种对大多数函数都适用的方法。这就引出了**“梯度算法”**。

我们先了解一下梯度下降是用来做什么的?

首先梯度下降(Gradient Descent, GD)，不是一个机器学习算法，而是一种基于搜索的最优化方法。梯度下降(Gradient Descent, GD)优化算法，其作用是用来对原始模型的损失函数进行优化，以便寻找到最优的参数，使得损失函数的值最小。

要找到使损失函数最小化的参数，如果纯粹靠试错搜索，比如随机选择1000个值，依次作为某个参数的值，得到1000个损失值，选择其中那个让损失值最小的值，作为最优的参数值，那这样太笨了。我们需要更聪明的算法，从损失值出发，去更新参数，且要大幅降低计算次数。

梯度下降算法作为一个聪明很多的算法，抓住了参数与损失值之间的导数，也就是能够计算梯度（gradient），通过导数告诉我们此时此刻某参数应该朝什么方向，以怎样的速度运动，能安全高效降低损失值，朝最小损失值靠拢。

(二)什么是梯度

简单地来说，多元函数的导数(derivative)就是梯度(gradient)，分别对每个变量进行微分，然后用逗号分割开，梯度是用括号包括起来，说明梯度其实一个向量，我们说损失函数L的梯度为：
$$\nabla L=(\frac{\partial L}{\partial a},\frac{\partial L}{\partial b})$$
我们知道导数就是变化率。梯度是向量，和参数维度一样。

假设，我们有一个二元函数$$f(x_1,x_2)=x_1^2+x_1{x}_2-3x_2$$ 。那么f的梯度为：$$\nabla f=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2})=(2x_1+x_2,x_1-3)$$

例如在点(1,2)，梯度∇f的取值为：
$$\nabla f(1,2)=(2\ast 1+2,1-3)=(4,-2)$$
那么这个梯度有什么用呢？

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。

梯度指向误差值增加最快的方向，导数为0（梯度为0向量）的点，就是优化问题的解。在上面的二元函数中，点(1,2)向着(4,2)的方向就是梯度方向 为了找到这个解，我们沿着梯度的反方向进行线性搜索，从而减少误差值。每次搜索的步长为某个特定的数值e，直到梯度与0向量非常接近为止。更新的点是x1=x0-e所有点的x梯度，y1=y0-e所有点的y梯度。

（三）理解梯度下降算法

很多求解最优化问题的方法，大多源自于模拟生活中的某个过程。比如模拟生物繁殖，得到遗传算法。模拟钢铁冶炼的冷却过程，得到退火算法。其实梯度下降算法就是模拟滚动，或者下山，在数学上可以通过函数的导数来达到这个模拟的效果。

梯度下降算法是一种思想，没有严格的定义。

1.场景假设

梯度下降就是从群山中山顶找一条最短的路走到山谷最低的地方。

既然是选择一个方向下山，那么这个方向怎么选？每次该怎么走？选方向在算法中是以随机方式给出的，这也是造成有时候走不到真正最低点的原因。如果选定了方向，以后每走一步，都是选择最陡的方向，直到最低点。

总结起来就一句话：随机选择一个方向，然后每次迈步都选择最陡的方向，直到这个方向上能达到的最低点。

梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：

一个人被困在山上，需要从山顶到山谷。但此时雾很大，看不清下山的路径。他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，随机选择一个方向，然后每次迈步都选择最陡的方向。然后每走一段距离，都反复采用同一个方法：如果发现脚下的路是下坡，就顺着最陡的方向走一步，如果发现脚下的路是上坡，就逆着方向走一步，最后就能成功的抵达山谷。

2.数学推导

从数学的角度出发，针对损失函数L，假设选取的初始点为（a_0,b_0）；现在将这个点稍微移动一点点(a_1,b_1)，得到。那么根据泰勒展开式（多元函数的一阶展开式）：
$$f(x_1,\dots ，x_n)=f(a_1,\dots ，a_n)+\sum _{i=1}^n\frac{\partial f(a_1,\dots ，a_n)}{\partial x_i}(x_i-a_i)+o(\sum _i|x_i-a_i|)$$

设我们移动的“一点点”为ΔL ，则我们可以得到ΔL=L(a_1,b_1)-L(a_0,b_0)，将泰勒展开式代入其中，我们则得到：
$$\Delta L=L(a_1,b_1)-L(a_0,b_0)\approx \frac{\partial L}{\partial a}\Delta a+\frac{\partial L}{\partial b}\Delta b$$

如果我们令移动的距离分别为： $$\Delta a=-\eta (\frac{\partial L}{\partial a}),\Delta b=-\eta (\frac{\partial L}{\partial b})$$

其中规定η>0，则可以得到：
$$\Delta L\approx -\eta [(\frac{\partial L}{\partial a}{)}^2+(\frac{\partial L}{\partial b}{)}^2]⩽0$$
这就说明，我们如果按照规定的移动距离公式移动参数，那么损失函数的函数值始终是下降的，这样就达到了我们要求的“损失变小”的要求了。如果一直重复这种移动，则可以证明损失函数最终能够达到一个最小值。

那么我们就可以得到损失函数值（也就是下一步的落脚点）的迭代公式：
$$(a_{k+1},b_{k+1})=(a_{k+1}-\eta \frac{\partial L}{\partial a},b_{k+1}-\eta \frac{\partial L}{\partial b})$$

针对于上述公式，有一些常见的问题：

为什么要梯度要乘以一个负号？

我们已经知道：梯度的方向就是损失函数值在此点上升最快的方向，是损失增大的区域，而我们要使损失最小，因此就要逆着梯度方向走，自然就是负的梯度的方向，所以此处需要加上负号。

关于参数 η:

我们已经知道，梯度对应的是下山的方向，而参数η对应的是步伐的长度。在学术上，我们称之为**“学习率”(learning rate)**，是模型训练时的一个很重要的超参数，能直接影响算法的正确性和效率：

• 首先，学习率η不能太大。因此从数学角度上来说，一阶泰勒公式只是一个近似的公式，只有在学习率很小，也就是Δa,Δb很小时才成立。并且从直观上来说，如果学习率η太大，那么有可能会“迈过”最低点，从而发生“摇摆”的现象（不收敛），无法得到最低点
• 其次，学习率η又不能太小。如果太小，会导致每次迭代时，参数几乎不变化，收敛学习速度变慢，使得算法的效率降低，需要很长时间才能达到最低点。

二、实现梯度下降（可视化）

（一）求导的方法

在python中有两种常见求导的方法，一种是使用Scipy库中的derivative方法，另一种就Sympy库中的diff方法。

1.Scipy

scipy.misc.derivative(func, x0, dx=1.0, n=1, args=(), order=3)[source]

在一个点上找到函数的第n个导数。即给定一个函数，请使用间距为dx的中心差分公式来计算x0处的第n个导数。

参数：

func：需要求导的函数，只写参数名即可，不要写括号，否则会报错
x0：要求导的那个点，float类型
dx（可选）：间距，应该是一个很小的数，float类型
n（可选）：n阶导数。默认值为1，int类型
args（可选）：参数元组
order（可选）：使用的点数必须是奇数，int类型
求一阶导数的例子：

from scipy.misc import derivative

def f(x):
    return x**3 + x**2
derivative(f, 1.0, dx=1e-6)
--------------
4.999999999921734

2. Sympy表达式求导
sympy是符号化运算库，能够实现表达式的求导。所谓符号化，是将数学公式以直观符号的形式输出。

import sympy as sy
# 符号化变量
x = sy.Symbol('x')

func = 1/(1+x**2)

print("x:", type(x))
print(func)
print(diff(func, x))
print(diff(func, x).subs(x, 3))
print(diff(func, x).subs(x, 3).evalf())
-----------
x: <class 'sympy.core.symbol.Symbol'>
1/(x**2 + 1)
-2*x/(x**2 + 1)**2
-3/50
-0.0600000000000000

(二)模拟实现梯度下降

1.封装函数

首先构造一个损失函数
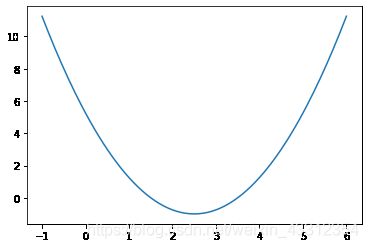
$$loss(x)=(x-2.5{)}^2-1$$ ，然后创建在-1到6的范围内构建140个点，并且求出对应的损失函数值，这样就可以画出损失函数的图形。

import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative

def lossFunction(x):
    return (x-2.5)**2-1

# 在-1到6的范围内构建140个点
plot_x = np.linspace(-1,6,141)
# plot_y 是对应的损失函数值
plot_y = lossFunction(plot_x)

plt.plot(plot_x,plot_y)
plt.show()

已知梯度下降的本质是多元函数的导数，这了定义一个求导的方法，使用的是scipy库中的derivative方法。

"""
算法：计算损失函数J在当前点的对应导数
输入：当前数据点theta
输出：点在损失函数上的导数
"""
def dLF(theta):
    return derivative(lossFunction, theta, dx=1e-6)

接下来我们就可以进行梯度下降的操作了。首先我们需要定义一个点θ 作为初始值，正常应该是随机的点，但是这里先直接定为0。然后需要定义学习率η ，也就是每次下降的步长。这样的话，点θ 每次沿着梯度的反方向移动η距离，即θ=θ-η*ᐁf ，然后循环这一下降过程。

那么还有一个问题：如何结束循环呢？梯度下降的目的是找到一个点θ，使得损失函数值最小，因为梯度是不断下降的，所以新的θ点对应的损失函数值在不断减小，但是差值会越来越小，因此我们可以设定一个非常小的数作为阈值，如果说损失函数的差值减小到比阈值还小，我们就认为已经找到了。

theta = 0.0
eta = 0.1
epsilon = 1e-6
while True:
    # 每一轮循环后，要求当前这个点的梯度是多少
    gradient = dLF(theta)
    last_theta = theta
    # 移动点，沿梯度的反方向移动步长eta
    theta = theta - eta * gradient
    # 判断theta是否达到最小值
    # 因为梯度在不断下降，因此新theta的损失函数在不断减小
    # 看差值是否达到了要求
    if(abs(lossFunction(theta) - lossFunction(last_theta)) < epsilon):
        break
print(theta)
print(lossFunction(theta))
---------
2.498732349398569
-0.9999983930619527

下面可以创建一个用于存放所有点位置的列表，然后将其在图上绘制出来。

为了方便测试，可以将其封装成函数进行调用。

def gradient_descent(initial_theta, eta, epsilon=1e-6):
    theta = initial_theta
    theta_history.append(theta)
    while True:
        # 每一轮循环后，要求当前这个点的梯度是多少
        gradient = dLF(theta)
        last_theta = theta
        # 移动点，沿梯度的反方向移动步长eta
        theta = theta - eta * gradient
        theta_history.append(theta)
        # 判断theta是否达到损失函数最小值的位置
        if(abs(lossFunction(theta) - lossFunction(last_theta)) < epsilon):
            break

def plot_theta_history():
    plt.plot(plot_x,plot_y)
    plt.plot(np.array(theta_history), lossFunction(np.array(theta_history)), color='red', marker='o')
    plt.show()

2.调整学习率

首先使用学习率η=0.1 进行观察

eta=0.1
theta_history = []
gradient_descent(0., eta)
plot_theta_history()
print("梯度下降查找次数：",len(theta_history))
-------
梯度下降查找次数： 35

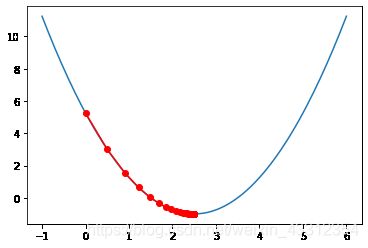
我们发现，在刚开始时移动比较大，这是因为学习率是一定的，再乘上梯度本身数值大（比较陡），后来梯度数值小（平缓）所以移动的比较小。且经历了34次查找。

使用使用学习率η=0.01 进行观察：

eta=0.01
theta_history = []
gradient_descent(0., eta)
plot_theta_history()
print("梯度下降查找次数：",len(theta_history))
---------
梯度下降查找次数： 310

可见学习率变低了，每一步都很小，因此需要花费更多的步数。

如果我们将学习率调大，会发生什么？

eta=0.9
theta_history = []
gradient_descent(0., eta)
plot_theta_history()
print("梯度下降查找次数：",len(theta_history))
---------
梯度下降查找次数：35

可见在一定范围内将学习率调大，还是会逐渐收敛的。但是我们要注意，如果学习率调的过大， 一步迈到“损失函数值增加”的点上去了，在错误的道路上越走越远（如下图所示），就会导致不收敛，会报OverflowError的异常。

为了避免报错，可以对原代码进行改进：

• 在计算损失函数值时捕获一场

def lossFunction(x):
    try:
        return (x-2.5)**2-1
    except:
        return float('inf')

• 设定条件，结束死循环

def gradient_descent(initial_theta, eta, n_iters, epsilon=1e-6):
    theta = initial_theta
    theta_history.append(theta)
    i_iters = 0
    while i_iters < n_iters:
        gradient = dLF(theta)
        last_theta = theta
        theta = theta - eta * gradient
        theta_history.append(theta)
        if(abs(lossFunction(theta) - lossFunction(last_theta)) < epsilon):
            break
        i_iters += 1

（三）小结

梯度是向量，求梯度就要求导数。在python中，除了自己手动计算以外，还有两个常用的求导方法：Scipy & Sympy。

• 在求出导数之后就可以模拟梯度下降的过程编写代码了，这里面还要注意退出循环的条件。
• 当学习率过小，收敛学习速度变慢，使得算法的效率降低；
• 学习率过大又会导致不收敛，在“错误的道路上”越走越远。我们要对异常进行进行处理。

三、线性回归中的梯度下降

（一）理论推导

1.目标

在多元线性回归中，其预测值为：
$$\widehat{y_i}={\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+\dots +{\theta }_n{X}_n^{(i)}$$
$$已知训练数据样本x、y，找到{\theta }_0,{\theta }_1,{\theta }_2,\dots ,{\theta }_n，使得损失函数尽可能小：$$
$$J=\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$
下面就要使用梯度下降法求多元线性回归中损失函数J的最小值。

2.整理损失函数

使用梯度下降法来求损失函数最小值时，要对损失函数进行一定的设计。

下面我们要进行一下化简。

将预测值$$\widehat{y_i}={\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+\dots +{\theta }_n{X}_n^{(i)}$$代入到损失函数J中，可以得到：
$$J=\sum _{i=1}^m(y^{(i)}-{\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+\dots +{\theta }_n{X}_n^{(i)}{)}^2$$

其中 $$\theta =({\theta }_0,{\theta }_1,{\theta }_2,\dots ,{\theta }_n)$$ 是列向量列向量，而且我们注意到，可以虚构第0个特征X_0，另其恒等于1，推导时结构更整齐，也更加方便：
$$\widehat{y_i}={\theta }_0{X}_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+\dots +{\theta }_n{X}_n^{(i)}$$
这样我们就可以改写成向量点乘的形式：
$$X_b=\left(\begin{array}{ccccc}1& X_1^{(1)}& X_1^{(1)}& \dots & X_n^{(1)}\\ 1& X_1^{(2)}& X_1^{(2)}& \dots & X_n^{(2)}\\ \dots & & & \dots & \dots \\ 1& X_1^{(m)}& X_1^{(m)}& \dots & X_n^{(m)}\end{array}\right)\theta =\left(\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ \dots \\ {\theta }_n\end{array}\right)$$

$$将X_b带入损失函数中，可以将其改写为：$$
$$J=\sum _{i=1}^m(y^{(i)}-{\theta }_0{X}_0^{(i)}+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+\dots +{\theta }_n{X}_n^{(i)}{)}^2$$
$$对{\theta }_n进行求导，可以得到:$$
$$ᐁJ(\theta )=\left(\begin{array}{c}\frac{\partial J}{\partial {\theta }_0}\\ \frac{\partial J}{\partial {\theta }_1}\\ \frac{\partial J}{\partial {\theta }_2}\\ \dots \\ \frac{\partial J}{\partial {\theta }_n}\end{array}\right)=\left(\begin{array}{c}{\sum }_{i=1}^{m}2(y^{(i)}-X_b^{(i)}{\theta }_0)\cdot (-1)\\ {\sum }_{i=1}^{m}2(y^{(i)}-X_b^{(i)}{\theta }_0)\cdot (-X_1^{(i)})\\ {\sum }_{i=1}^{m}2(y^{(i)}-X_b^{(i)}{\theta }_0)\cdot (-X_2^{(i)})\\ \dots \\ {\sum }_{i=1}^{m}2(y^{(i)}-X_b^{(i)}{\theta }_0)\cdot (-X_n^{(i)})\end{array}\right)=2\left(\begin{array}{c}{\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_1^{(i)}\\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_2^{(i)}\\ \dots \\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_n^{(i)}\end{array}\right)$$
在上式中梯度大小实际上是和样本数量m相关，m越大，累加之和越大，这是不合理的；为了使与m无关，除以m。
于是演变成：
$$使损失函数\frac{1}{m}\sum _{i=1}^m(y^i-{\hat{y}}^i{)}^2尽可能小。同时注意到，损失函数变成了均方误差MSE：J(\theta )=MSE(y,\hat{y})。$$
对其求导，有：
$$ᐁJ(\theta )=\frac{2}{m}\cdot \left(\begin{array}{c}{\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_1^{(i)}\\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_2^{(i)}\\ \dots \\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_n^{(i)}\end{array}\right)=\frac{2}{m}\cdot \left(\begin{array}{c}{\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_0^{(i)}\\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_1^{(i)}\\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_2^{(i)}\\ \dots \\ {\sum }_{i=1}^m(X_b^{(i)}{\theta }_0-y^{(i)})\cdot X_n^{(i)}\end{array}\right)$$
我们将这个复杂的表达式再一次进行分解，可以写成向量
$$\frac{2}{m}\cdot (X_b^{(1)}-y^{(1)},X_b^{(2)}-y^{(2)},X_b^{(3)}-y^{(3)},\dots ,X_b^{(m)}-y^{(m)})$$
$$再去点乘矩阵X_b：$$
$$\cdot \left(\begin{array}{ccccc}{X}_0^{(1)}& X_1^{(1)}& X_2^{(1)}& \dots & X_n^{(1)}\\ X_0^{(2)}& X_1^{(2)}& X_2^{(2)}& \dots & X_n^{(2)}\\ X_0^{(3)}& X_1^{(3)}& X_2^{(3)}& \dots & X_n^{(3)}\\ \dots & & & \dots & \dots \\ X_0^{(m)}& X_1^{(m)}& X_2^{(m)}& \dots & X_n^{(m)}\end{array}\right)$$

$$即：将求梯度的过程转换为两个矩阵之间的乘法运算：1\ast m的向量乘以m\ast (n+1)的矩阵，得到1\ast (n+1)的向量。其结果是\frac{2}{m}(X_b\theta -y{)}^T{X}_b$$。

然后这里还需要一个转秩。为什么转秩？本来应该是一个列向量，但是这里需要转秩成行向量。因为得到的是1*(n+1)的行向量，梯度是(n+1)*1的列向量，因此需要再次进行转秩（分别转秩，再交换位置）。

3.最终得到的梯度

最终得到梯度结果为：
$$ᐁJ(\theta )=\frac{2}{m}{X}_b^T(X_b\theta -y)$$

(二)梯度下降代码演示

1.梯度下降代码

下面就可以整合梯度下降的代码，将上面推导出来的梯度结果的表达式带入梯度下降的流程中。

def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
    """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
    assert X_train.shape[0] == y_train.shape[0], \
        "the size of X_train must be equal to the size of y_train"

    def J(theta, X_b, y):
        try:
            return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
        except:
            return float('inf')
        
    def dJ(theta, X_b, y):
        return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

    def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

        theta = initial_theta
        cur_iter = 0

        while cur_iter < n_iters:
            gradient = dJ(theta, X_b, y)
            last_theta = theta
            theta = theta - eta * gradient
            if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                break

            cur_iter += 1

        return theta

    X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
    initial_theta = np.zeros(X_b.shape[1])
    self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

    self.intercept_ = self._theta[0]
    self.coef_ = self._theta[1:]

    return self

2.使用真实数据出现的问题

下面准备波士顿房产数据，准备进行验证

import numpy as np
from sklearn import datasets

boston = datasets.load_boston()
X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

首先使用线性回归中的“标准方程解”进行计算，得到相应系数与截距的最优值，然后计算回归评分（R方）：

from myAlgorithm.LinearRegression import LinearRegression
from myAlgorithm.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

lin_reg1 = LinearRegression()
%time lin_reg1.fit_normal(X_train, y_train)
lin_reg1.score(X_test, y_test)

----------
输出：
CPU times: user 25.7 ms, sys: 25.5 ms, total: 51.2 ms
Wall time: 116 ms
0.8129802602658466

然后创建一个lin_reg2，使用梯度下降法得到最优参数：

lin_reg2 = LinearRegression()
lin_reg2.fit_gd(X_train, y_train, )
lin_reg2.coef_
----------
输出：
array([nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan])

发现在执行的过程中有一个RuntimeWarning的警告overflow。并且得到的全都是空。

这是因为，在一个真实的数据中，查看前3行数据，就可以观察到，每一个特征所对应的规模是不一样的，有一些很小，有一些很大，使用默认的学习率可能过大，导致不收敛。

下面我们传递一个很小的学习率来看一下结果：

lin_reg2.fit_gd(X_train, y_train, eta=0.000001)
lin_reg2.score(X_test, y_test)
--------------
输出：
0.27556634853389195

我们发现得到的R方评分很差，这可能是因为学习率设置的过小，步长太小没有到最优值。为了验证这个假设，可以再进行一次验证：

lin_reg2.fit_gd(X_train, y_train, eta=0.000001, n_iters=1e6)
lin_reg2.score(X_test, y_test)
------
输出：
0.75418523539807636

我们发现，即使计算了这么久，其结果还是没有“标准方程解”的评分高。

对于这种情况应该怎么办呢？之前已经分析出来了，之所以出现这种现象，是因为真实数据整体不在一个规模上，解决的方式，就是在梯度下降之前进行数据归一化。

3.数据归一化

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_std = standardScaler.transform(X_train)
lin_reg3 = LinearRegression()
lin_reg3.fit_gd(X_train_std, y_train)
X_test_std = standardScaler.transform(X_test)
lin_reg2.score(X_test, y_test)
--------
输出：
0.8129802602658466

这和“正规方程解”得到的score一样，这就说明我们找到了损失函数的最小值。

（三）小结

• $$对多元线性回归的损失函数进行求导，其结果是\frac{2}{m}(X_b\theta -y{)}^T{X}_b。$$
• 然后使用向量化的方式编写代码，但是发现在真实数据中效果比较差，这是因为数据的规模不一样，因此在梯度下降之前需要使用归一化。

四、速度更快的随机梯度下降法

在之前学习的梯度下降法的步骤中，在每次更新参数时是需要计算所有样本的，通过对整个数据集的所有样本的计算来求解梯度的方向。这种计算方法被称为：批量梯度下降法BGD(Batch Gradient Descent)。但是这种方法在数据量很大时需要计算很久。

针对该缺点，有一种更好的方法：随机梯度下降法SGD（stochastic gradient descent），随机梯度下降是每次迭代使用一个样本来对参数进行更新。虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。但是相比于批量梯度，这样的方法更快，我们也是可以接受的。下面就来学学看看随机梯度下降法。

（一）理解随机梯度下降

1.随机取值的公式推导

批量梯度下降法，每一次计算过程，都要将样本中所有信息进行批量计算。但是显然如果样本量很大的话，计算梯度就比较耗时。基于这个问题，改进的方案就是随机梯度下降法。即每次迭代随机选取一个样本来对参数进行更新。使得训练速度加快。

下面我们从数学的角度来看：我们将原本的矩阵中根据样本数量求和这一操作去掉，同样也就不需要除以m了。

最终我们得到损失函数的进行求导，得到的结果为：
$$2(X_b^{(i)}{)}^T(X_b^{(i)}-y^{(i)})$$
要注意，得到的向量是搜索方向，不是梯度方向，因此已经不是算是函数的梯度了。

2.随机下降与学习率的取值

其过程就是：每次随机取出一个i，得到一个向量，沿着这个随机产生的向量的方向进行搜索，不停的迭代，得到的损失函数的最小值。

随机梯度下降法的搜索过程如下图所示。如果是批量搜索，那么每次都是沿着一个方向前进，但是随机梯度下降法由于不能保证随机选择的方向是损失函数减小的方向，更不能保证一定是减小速度最快的方向，所以搜索路径就会呈现下图的态势。即随机梯度下降有着不可预知性。

但实验结论告诉我们，通过随机梯度下降法，依然能够达到最小值的附近（用精度换速度）。

随机梯度下降法的过程中，学习率η的取值很重要，这是因为如果学习率一直取一个固定值，所以可能会导致点θ已经取到最小值附近了，但是固定的步长导致点的取值又跳去了这个点的范围。因此我们希望在随机梯度下降法中，学习率η是逐渐递减的。

设计一个函数，使学习率η随着下降循环次数的增加而减小。

我们想到最简单的表示方法是一个倒数的形式$$\eta =\frac{1}{i_{i}ter}$$，不过这样也会有问题，如果循环次数i_iter比较小的时候，学习率下降的太快了，比如循环次数为1变为2，则学习率减少50%。因此我们可以将分子变为常数t0，并在分母上增加一个常数项t1来$$\eta =\frac{t_0}{i_{i}ter+t_1}$$来缓解初始情况下，学习率变化太大的情况，且更灵活。

(二)BGD&SGD效果比较

下面可以我们要对比一下，批量梯度下降算法和随机梯度下降算法的比较。我们主要观察运行时间和迭代次数这两个指标。

1.批量梯度下降法代码

import numpy as np
import matplotlib.pyplot as plt

m = 100000
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 4. * x + 3. + np.random.normal(0, 3, size=m)

def J(theta, X_b, y):
    try:
        return np.sum((y-X_b.dot(theta)) ** 2) / len(y)
    except:
        return float('inf')

def dJ(theta, X_b, y):
    return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-6):
    theta = initial_theta
    cur_iter = 0
    while(cur_iter < n_iters):
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break
        cur_iter += 1
    return theta

%%time
X_b = np.hstack([np.ones((len(X),1)),X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
theta

2.随机梯度下降

首先，计算损失函数的求导结果时，传递的不是整个矩阵X_b和整个向量y，而是其中一行
X_b_i
、其中的一个数值，因此表达式为X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.

然后我们可以内置一个计算学习率的函数，即使用来缓解初始情况下，学习率变化太大的情况。

最后就是终止循环条件的差异了。在批量梯度下降的计算过程中，循环终止的条件有两个，第一个是循环次数达到上限while(cur_iter $$abs(J(theta,X_b,y)-J(lasttheta,X_b,y))<epsilon$$
那么在随机梯度下降中，由于梯度下降的方向是随机的，所以损失函数不能保证一直减小，有可能是跳跃的，因此就不要第二个条件了，直接使用for循环判断迭代次数就好了。

# 传递的不是整个矩阵X_b，而是其中一行X_b_i;传递y其中的一个数值y_i
def dJ_sgd(theta, X_b_i, y_i):
    return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.

def sgd(X_b, y, initial_theta, n_iters):
    t0 = 5
    t1 = 50
    # 
    def learning_rate(cur_iter):
        return t0 / (cur_iter + t1)
    theta = initial_theta

    for cur_iter in range(n_iters):
        # 随机找到一个样本（得到其索引）
        rand_i = np.random.randint(len(X_b))
        gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
        theta = theta - learning_rate(cur_iter) * gradient
    return theta

%%time
X_b = np.hstack([np.ones((len(X),1)),X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b, y, initial_theta, n_iters=len(X_b)//3)
print(theta)

"""
输出：
[2.9287233  4.05019715]
CPU times: user 296 ms, sys: 6.49 ms, total: 302 ms
Wall time: 300 ms
"""

3.分析

通过简单的例子，我们可以看出，在批量梯度下降的过程中消耗时间1.73 s，而在随机梯度下降中，只使用300 ms。并且随机梯度下降中只考虑的三分一的样本量，且得到的结果一定达到了局部最小值的范围内

(三)代码实现

1. 改进后的代码

在上一小节，为了比较批量梯度下降和随机梯度下降，我们进行了简单的实现，但实际上对于随机梯度下降法还是有一些问题的。

在之前，只是简单的只考虑的三分一的样本量，实际上我们已经考虑所有的样本量n次，然后在每次考虑样本量时采用随机的方式。

我们首先要了解：n_iters表示对所有样本的循环次数，所有样本的个数为m。因此我们在循环时，应该使用双重循环，即外层循环为每次循环所有样本，内层循环为在所有样本中进行随机选择，次数为样本数量。那么要注意：在计算学习率时，次数就变为

def fit_sgd(self, X_train, y_train, n_iters=50, t0=5, t1=50):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        assert n_iters >= 1

        def dJ_sgd(theta, X_b_i, y_i):
            return X_b_i * (X_b_i.dot(theta) - y_i) * 2.

        def sgd(X_b, y, initial_theta, n_iters=5, t0=5, t1=50):

            def learning_rate(t):
                return t0 / (t + t1)

            theta = initial_theta
            m = len(X_b)
            for i_iter in range(n_iters):
                # 将原本的数据随机打乱，然后再按顺序取值就相当于随机取值
                indexes = np.random.permutation(m)
                X_b_new = X_b[indexes,:]
                y_new = y[indexes]
                for i in range(m):
                    gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
                    theta = theta - learning_rate(i_iter * m + i) * gradient

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.random.randn(X_b.shape[1])
        self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

2.使用自己的SGD

import numpy as np
from sklearn import datasets

boston = datasets.load_boston()
X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

from myAlgorithm.LinearRegression import LinearRegression
from myAlgorithm.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_std = standardScaler.transform(X_train)
X_test_std = standardScaler.transform(X_test)
lin_reg1 = LinearRegression()
lin_reg1.fit_sgd(X_train, y_train, n_iters=2)
lin_reg1.score(X_test_std, y_test)
"""
输出：
0.78651716204682975
"""

通过增加n_iters的值，可以获得更好的结果：

lin_reg1.fit_sgd(X_train, y_train, n_iters=100)
lin_reg1.score(X_test_std, y_test)
"""
输出：
0.81294846132723497
"""

3.sklearn中的SGD

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor()    # 默认n_iter=5
%time sgd_reg.fit(X_train_std, y_train)
sgd_reg.score(X_test_std, y_test)

增加迭代次数，可以提升效果

sgd_reg = SGDRegressor(n_iter=100)
%time sgd_reg.fit(X_train_std, y_train)
sgd_reg.score(X_test_std, y_test)

sklearn中的算法实现，其实和我们的实现有很大的区别，进行了很多的优化。我们只是简单的实现了它的原理。

（四）小结

批量梯度下降法BGD(Batch Gradient Descent)。

• 优点：全局最优解；易于并行实现；
• 缺点：当样本数据很多时，计算量开销大，计算速度慢。

针对于上述缺点，其实有一种更好的方法：随机梯度下降法SGD（stochastic gradient descent），随机梯度下降是每次迭代使用一个样本来对参数进行更新。

• 优点：计算速度快；
• 缺点：收敛性能不好。

五、梯度下降的调试方式及总结

梯度下降法的使用，一个非常重要的步骤是：我们要求出定义的损失函数某一点θ上对应的梯度是什么。在复杂函数的情况下，求导得到梯度并不容易。如果我们梯度的计算错误了，在后续的程序中也不会报错。那么我们如何去发现这个错误呢？

介绍一种简单的方法，能够对梯度下降法中求梯度的公式推导进行调试。

（一）调试原理

以一维为例，求某一点（红色）相应的梯度值（导数），就是曲线在这个点上切线的斜率。我们可以使用距离该点左右两侧θ+ε，θ-ε的两个蓝色点的连线的斜率，作为红点处切线斜率。

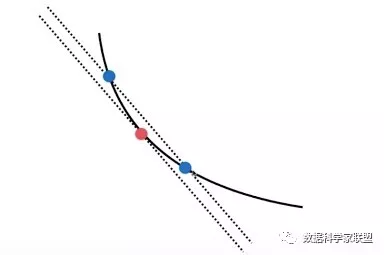
这样就可以将近似地得到点θ的梯度为，两个蓝点纵向坐标差除以横向坐标差：
$$\frac{dJ}{d\theta }=\frac{J(\theta +\epsilon )-J(\theta -\epsilon )}{2\epsilon }$$

推广到多维函数中，对于点θ=(θ0,θ1,…，θn)，则对损失函数进行求导，为：$$\frac{dJ}{d\theta }=(\frac{dJ}{d{\theta }_0},\frac{dJ}{d{\theta }_1},\dots ，\frac{dJ}{d{\theta }_n})$$。

在计算时，要分别计算每个维度上的点，以维度θ0为例，得到在该维度上距离该店非常距离非常近的左右两点：$${\theta }_0^{+}=({\theta }_0+\epsilon ,{\theta }_1,\dots \dots ,{\theta }_n)、{\theta }_0^{-}=({\theta }_0-\epsilon ,{\theta }_1,\dots \dots ,{\theta }_n)。$$这样可以得到：
$$\frac{dJ}{d\theta }=\frac{J({\theta }_0^{+})-J({\theta }_0^{-})}{2\epsilon }$$

对于每一个维度，都按照上述的方法计算梯度，最后再组合起来，得到最终的梯度。但是这样的求法，从数学上来看比较直观。但是因为每个维度上都要求两次带入，因此时间复杂度变高了。

这种方法作为一个调试的手段，在还未完成时，可以使用小数据量，进行计算，得到最终结果。然后再通过推导公式的方式得到的梯度结果，是否和其相同。

(二)使用展示

下面我们在一组数据上，分别使用数学公式法和调试法来计算梯度，主要观察其结果与所消耗的时间。

# 首先定义损失函数
def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta))**2) / len(X_b)
    except:
        return float('inf')

# 使用数学公式推导的方式，求损失函数J在参数theta上的梯度
def dJ_math(theta, X_b, y):
    return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

# 使用上文提到的梯度调试的方法
def dJ_debug(theta, X_b, y, epsilon=0.01):
    # 先创建一个与参数组等长的向量
    res = np.empty(len(theta))
    # 对于每个梯度，求值
    for i in range(len(theta)):
        theta_1 = theta.copy()
        theta_1[i] += epsilon
        theta_2 = theta.copy()
        theta_2[i] -= epsilon
        res[i] = (J(theta_1, X_b, y) - J(theta_2, X_b, y)) / (2 * epsilon)
    return res

# 梯度下降的过程
def gradient_descent(dJ, X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
    theta = initial_theta
    cur_iter = 0
    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break          
        cur_iter += 1
    return theta

然后我们先调用dJ_debug函数，看看正确的梯度结果是什么

X_b = np.hstack([np.ones((len(X), 1)), X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
%time theta = gradient_descent(dJ_debug, X_b, y, initial_theta, eta)
theta

然后我们再调用dJ_math，来检验我们的求导公式对不对：

%time theta = gradient_descent(dJ_math, X_b, y, initial_theta, eta)
theta

最终发现，我们求得的梯度公式得到的答案是正确的。

但是观察到，使用debug的方式要比用求导公式的执行时间慢很多，如果在真实数据集上，可能会差的更多了。因此我们在求梯度的时候，可以用这种通用的debug方式先在小数据集上对求导公式进行检验。

(三)对梯度下降法的总结

我们学习了两种梯度下降法：

• 批量梯度下降法 Batch Gradient Descent
• 随机梯度下降法 Stochastic Gradient Descent

批量梯度下降法每次对所有样本都看一遍，缺点是慢，缺点是稳定。随机梯度下降法每次随机看一个，优点是快，缺点是不稳定。

其实还有一种中和二者优缺点的方法小批量梯度下降法 MBGD（Mini-Batch Gradient Descent）：在每次更新时用b个样本，其实批量的梯度下降就是一种折中的方法，用一些小样本来近似全部。优点：减少了计算的开销量，降低了随机性。

在机器学习领域，随机具有非常大的意义，因为计算速度很快。对于复杂的损失函数来说，随机可以跳出局部最优解，并且有更快的速度。