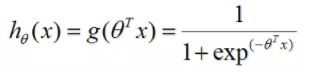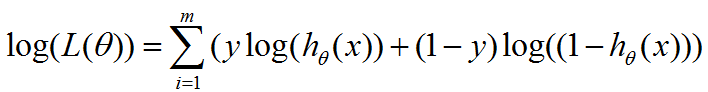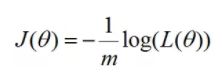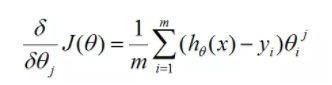机器学习逻辑回归：算法兑现为python代码

戳上面的蓝字关注我们！

作者：alg-flody

编辑：Emily

    0 回顾

昨天推送了逻辑回归的基本原理：从逻辑回归的目标任务，到二分类模型的构建，再到如何用梯度下降求出二分类模型的权重参数。今天，我们将对这个算法兑现为代码，包括用于模拟数据集的生成，到模型的创建，权重参数的求解。这个过程是动手实践写代码的过程，这很有趣！

    1 生成模拟的数据集

为了编写代码模拟二分类任务，我们的第一步工作是先生成用于测试的数据集，当然这一步也可以从网上找相关二分类任务的实际数据集。

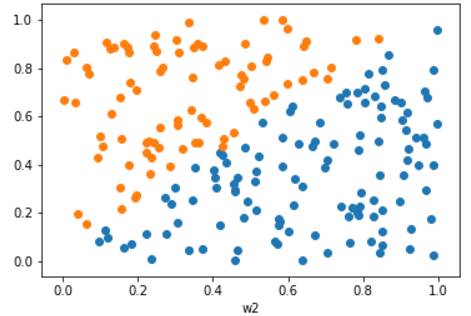
首先看下生成的用于模拟的数据集长得样子，它有两个特征w1，w2组成，共有200个样本点，现在的任务是要对这个数据集进行分类。

下面是用于模拟上图数据的代码：

import numpy as np

import matplotlib.pyplot as plt

#按照一定规律均匀分布含有两个特征的数据点

def createData(samplecnt,coef=1.0,intercept=0.05):

    x1 = np.random.uniform(0,1,samplecnt)

    x2 = np.random.uniform(0,1,samplecnt)

    index = (x2-intercept)/x1

    x1_pos = x1[index]

    x2_pos = x2[index]

    index = (x2-intercept)/x1 >=coef

    x1_neg = x1[index]

    x2_neg = x2[index]

    plt.xlabel("w1")

     plt.ylabel("w2")

    plt.scatter(x1_pos,x2_pos)

    plt.scatter(x1_neg,x2_neg)

    regx = np.linspace(0,1,samplecnt)

    regy = coef*regx+intercept

    #plt.plot(regx,regy,color='g')

    plt.show()

    return x1_pos,x1_neg,x2_pos,x2_neg

#组合成原始数据

def combine_data(x1_pos,x1_neg,x2_pos,x2_neg):

    x1_pos_1 = x1_pos.reshape(-1,1)

    x2_pos_1 = x2_pos.reshape(-1,1)

    x_pos = np.concatenate((x1_pos_1,x2_pos_1),axis=1)

    x_pos_shape =  np.shape(x_pos)

    y_pos = np.ones(x_pos_shape[0])

    y_pos = y_pos.reshape(-1,1)

    data_pos = np.concatenate((x_pos,y_pos),axis=1)

    x1_neg_1 = x1_neg.reshape(-1,1)

    x2_neg_1 = x2_neg.reshape(-1,1)

    x_neg = np.concatenate((x1_neg_1,x2_neg_1),axis=1)

    x_neg_shape =  np.shape(x_neg)

    y_neg = np.zeros(x_neg_shape[0])

    y_neg = y_neg.reshape(-1,1)

    data_neg = np.concatenate((x_neg,y_neg),axis=1)

    data = np.vstack((data_pos,data_neg))

    data = np.random.permutation(data)

    return data

因此data表示以上所有的样本点和标签值组成的数据集，下面看下前10天长的样子：

             w1                  w2                y

array([[ 0.78863156,  0.45879449,  1.        ],

       [ 0.70291388,  0.03437041,  1.        ],

       [ 0.89775764,  0.24842968,  1.        ],

       [ 0.92674416,  0.13579184,  1.        ],

       [ 0.80332783,  0.71211063,  1.        ],

       [ 0.7208047 ,  0.48432214,  1.        ],

       [ 0.8523947 ,  0.06768344,  1.        ],

       [ 0.49226351,  0.24969169,  1.        ],

       [ 0.85094261,  0.79031018,  1.        ],

       [ 0.76426901,  0.07703571,  1.        ]])

下面介绍，如何用梯度下降法，求出两个特征对应的权重参数，进而能正确的预测，当一个新的样本点来的时候，能预测出属于0类，还是1类。

 

  2 梯度下降求权重参数

逻辑回归的模型，代价函数，梯度，昨天我们都已经准备好了，接下来，就是编写python 代码实现梯度下降的求解。

设定一个学习率迭代参数，当与前一时步的代价函数与当前的代价函数的差小于阈值时，计算结束，我们将得到3个权重参数，其中包括两个特征的权重参数，和偏置项的权重参数。

假定模型的决策边界为线性模型，梯度下降求逻辑回归模型的权重参数的基本思路如下：

 'model' 建立的逻辑回归模型：包括Sigmoid映射

'cost' 代价函数

'gradient'  梯度公式

'theta update'  参数更新公式

'stop stratege'  迭代停止策略：代价函数小于阈值法

下面分别将昨天准备好的公式，兑现为相应的代码：

不要忘记初始化一列偏置项：

做一个偏移量和2个特征的组合，这样与前面推送的理论部分衔接在一起，组合的代码如下所示：

'偏移量 b shape=(200,1)'

b = np.ones(200)

'将偏移量与2个特征值组合 shape = (200,3)'

X = np.hstack((b,X))

'model'

def sigmoid(x):

    return 1/(1+ np.exp(-x))

def model(theta,X):

    theta = np.array(theta)

    return sigmoid( X.dot(theta) )

'cost'

def cost(m,theta,X,y):

    ele = y*np.log(model(theta,X)) + (1-y)*np.log(1-model(theta,X))

    item_sum = np.sum(ele)

    return -item_sum/m

'gradient'

def gradient(m,theta,X,y,cols):

    grad_theta = []

    for j in range(cols):

        grad = (model(theta,X) - y).dot(X[:,j])

        grad_sum = np.sum(grad)    

        grad_theta.append(grad_sum/m)

    return np.array(grad_theta)

'theta update'

def theta_update(grad_theta,theta,sigma):

    return theta - sigma * grad_theta

'stop stratege'

def stop_stratege(cost,cost_update,threshold):

    return cost-cost_update < threshold

'逻辑回归算法'

def LogicRegression(X,y,threshold,m,xcols):

    start = time.clock()

    '设置权重参数的初始值'

    theta = np.zeros(xcols)

    '迭代步数'

    iters = 0;

    '记录代价函数的值'

    cost_record=[]

    '学习率'

    sigma = 0.01

    cost_val = cost(m,theta,X,y)

    cost_record.append(cost_val)

    while True:

        grad = gradient(m,theta,X,y,xcols)

        '参数更新'

        theta = theta_update(grad,theta,sigma)

        cost_update = cost(m,theta,X,y)

        if stop_stratege(cost_val,cost_update,threshold):

            break

        iters=iters+1

        cost_val = cost_update

        print("cost_val:%f" %cost_val)

        cost_record.append(cost_val)

    end = time.clock()

    print("LogicRegressionconvergence duration: %f s" % (end - start))

    return cost_record, iters,theta

   3 分析结果

调用逻辑回归函数：LogicRegression(data[:,[0,1,2]],data[:,3],0.00001,200,3)

结果显示经过，逻辑回归梯度下降经过如下时间得到初步收敛，LogicRegression convergence duration:18.076398 s，经过 56172万 多个时步迭代，每个时步计算代价函数的取值，如下图所示：

收敛时，得到的权重参数为：

array([ 0.48528656,  9.48593954, -9.42256868])  

参数的含义：第一个权重参数为偏置项，第二、三个权重参数相当，只不过贡献方向相反而已。

下面画出，二分类的决策边界，

plt.scatter(x1_pos,x2_pos)

plt.scatter(x1_neg,x2_neg)

wp = np.linspace(0.0,1.0,200)

plt.plot(wp,-(theta[0]+theta[1]*wp)/theta[2],color='g')

plt.show()

可以看到分类效果非常不错。

   4 总结

以上是逻辑回归的梯度下降求解思路和代码实现，在梯度下降的过程中，学习率和迭代终止的阈值属于这个算法的超参数，在本次调试过程中，心得如下：

1. 如果代价函数的最后稳定的值，确认比较大，比如0.5，说明模型中一定存在某些bug，比如在我调试过程中，将标签值错误地被赋值了第三列，实际应该为第四列，所以导致最后迭代终止时的成本值为0.50。

2. 学习率直接关系到迭代速度，如果学习率太小，迭代下降的会很慢，相反会比较快。

3. 迭代终止的策略选取，一般会根据迭代次数，成本函数前后两次的差小于某个阈值等，如果选取的终止策略不当，会导致看似收敛，实际成本值还很大的情况。

明天，让我们一起探讨下另一种分类策略，决策树的分类原理吧。

让我们看一下远边的大海，和海边优美的风景，先放松一下吧！

谢谢您的阅读，期待您的到来。

欢迎关注《算法channel》

主要推送关于算法的分析过程及应用的消息。培养思维能力，注重过程，挖掘背后的原理，刨根问底。本着严谨和准确的态度，目标是撰写实用和启发性的文章，欢迎您的关注。