opencv图像分析与处理(12)-逆滤波、维纳滤波、约束最小二乘方滤波和几何均值滤波
本节为opencv数字图像处理(12):图像复原与重建的第三小节,逆滤波、维纳滤波、约束最小二乘方滤波和几何均值滤波,主要包括:四种滤波复原图像的数学推导以及维纳滤波的C++实现。
1. 逆滤波器
emsp; 若退化函数已知或可以得到一个估计,最简单的图像复原方法就是直接做逆滤波,用退化函数除退化图像的傅立叶变换来计算原始图形的傅立叶变换的估计即:
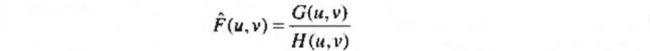
展开计算为:
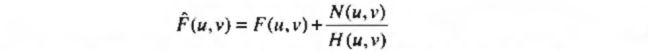
如果退化噪声为0或很小,噪声就会支配估计值 F ^ ( u , v ) \hat F(u,v) F^(u,v),这时候经常需要限制滤波的频率,使其接近原点。
1. 最小均方误差滤波/维纳滤波
这种滤波方法建立在图像和噪声都是随机变量的基础上,目标是找出未污染图像 f ( x , y ) f(x,y) f(x,y)的一个估计 f ^ \hat f f^,使它们之间的均方误差最小,误差度量由下式给出:
![]()
假设噪声和图像不相关,二者中有一个有零均值且估计中的灰度级是退化图像中灰度级的线性函数,则误差函数的最小值在频率与中由下式给出:

这个结果就是维纳滤波,方括号中的项组成的滤波器称为最小均方差滤波器或最小二乘误差滤波器。式子中: H ( u , v ) = H(u,v)= H(u,v)=退化函数; H ∗ ( u , v ) H*(u,v) H∗(u,v)= H ( u , v ) H(u,v) H(u,v)的复共轭; ∣ H ( u , v ) ∣ 2 = H ∗ ( u , v ) H ( u , v ) |H(u,v)|^2=H*(u,v)H(u,v) ∣H(u,v)∣2=H∗(u,v)H(u,v); S e t a ( u , v ) = ∣ N ( u , v ) ∣ 2 = S_{eta}(u,v)=|N(u,v)|^2= Seta(u,v)=∣N(u,v)∣2=噪声的功率谱。
如果噪声为0,那么噪声功率谱消失,维纳滤波简化为逆滤波。
信噪比是一个基于噪声和未退化图像的功率谱为基础的,频率域可用下式近似:

携带低噪声的图像SNR较高,是表征复原算法的性能的一个重要量度。
均方误差也可以这样描述:

而如果把复原图像考虑为“信号”,复原图像和原图像的差考虑为噪声,则空间域中信噪比可定义如下:

f f f和 f ^ \hat f f^越接近,这个比值越大。【这个定量与感觉上的图像质量没有很好的必然关系】
当处理白噪声时 ∣ N ( u , v ) ∣ 2 |N(u,v)|^2 ∣N(u,v)∣2是一个常数,但是未退化图像和噪声的功率谱通常未知或不能估计,则可用下式近似:
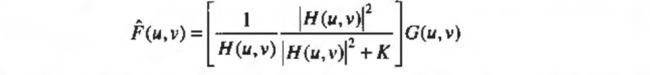
C++实现来自这篇博文:
#include 2. 约束最小二乘方滤波
虽然维纳滤波中可以根据上式来进行估计,但是很少得到合适的解,我们将图像受噪声污染表达为如下的矩阵形式:
g = H f + η g=Hf+\eta g=Hf+η
考虑一个带约束的最小准则函数 C C C,定义如下:

约束为:
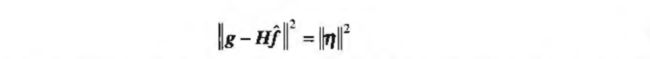
在频率域这个最佳化问题的解决方案由如下公式给出:
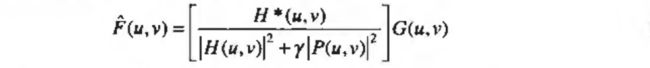
γ \gamma γ是一个参数,调整以满足上2式, P ( u , v ) P(u,v) P(u,v)是函数:

的傅立叶变换,当 γ = 0 \gamma=0 γ=0时最小二乘方滤波退化为直接逆滤波。
γ \gamma γ可以交互地手动调整,当然也可以迭代计算,步骤如下。
定义一个残差向量 r r r为:
![]()
由上3式知, F ^ ( u , v ) \hat F(u,v) F^(u,v)是 γ \gamma γ的函数,所以 r r r是该参数的函数,可以证明:
![]()
是 γ \gamma γ的单调递增函数,我们需要调整 γ \gamma γ使得:
![]()
若 ∣ ∣ r ∣ ∣ 2 = ∣ ∣ η ∣ ∣ 2 ||r||^2=||\eta||^2 ∣∣r∣∣2=∣∣η∣∣2,那么可以严格满足上述约束,具体地,寻找一个 γ \gamma γ值得方法:
- 指定 γ \gamma γ的初始值
- 计算 ∣ ∣ r ∣ ∣ 2 ||r||^2 ∣∣r∣∣2
- 满足上1式则停止;否则,若 ∣ ∣ r ∣ ∣ 2 < ∣ ∣ η ∣ ∣ 2 − a ||r||^2<||\eta||^2-a ∣∣r∣∣2<∣∣η∣∣2−a,增大 γ \gamma γ,若 ∣ ∣ r ∣ ∣ 2 = ∣ ∣ η ∣ ∣ 2 + a ||r||^2=||\eta||^2+a ∣∣r∣∣2=∣∣η∣∣2+a,则减少 γ \gamma γ。然后返回步骤2。重新计算最佳估计 F ^ ( u , v ) \hat F(u,v) F^(u,v)
上面步骤中,为了计算 ∣ ∣ r ∣ ∣ 2 ||r||^2 ∣∣r∣∣2,由上式3【从此处向上数第三个列出的公式】有:
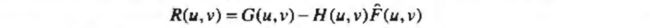
计算 R ( u , v ) R(u,v) R(u,v)的傅里叶反变换得 r ( x , y ) r(x,y) r(x,y),有:
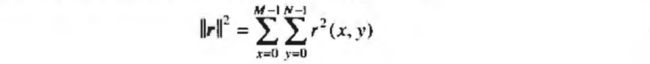
计算 ∣ ∣ η ∣ ∣ 2 ||\eta||^2 ∣∣η∣∣2的话,首先考虑正负图像的噪声方差:

其中:

为样本均值。注意到上2式【从此处向上数第二个列出的公式】的双重求和即为 ∣ ∣ η ∣ ∣ 2 ||\eta||^2 ∣∣η∣∣2,给出如下表达式:

也就是说,仅仅使用噪声的均值和方差的知识,就可以实现一个最佳复原算法,但必须假设噪声和图像灰度值不相关。但是需要指出,约束最小二乘方意义小的最佳复原并不是视觉效果上最好。
3. 几何均值滤波
几何均值滤波是维纳滤波的推广:
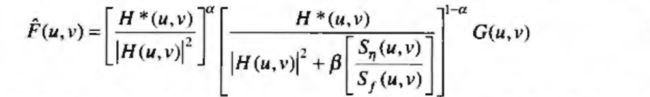
当 α = 1 \alpha=1 α=1,退化为直接逆滤波,当 α = 0 \alpha=0 α=0,参数维纳滤波器,参数维纳滤波器在 β = 1 \beta=1 β=1时还原为标准的维纳滤波器。如果 α = 1 / 2 \alpha=1/2 α=1/2,则滤波器变成相同幂次的两个量的积,也就是几何均值的定义。当 β = 1 \beta=1 β=1,随着 α \alpha α减小到 1 / 2 1/2 1/2以下,滤波器性能越来越接近逆滤波器,增大到 1 / 2 1/2 1/2以上,越来越接近维纳滤波器。当 α = 1 / 2 \alpha=1/2 α=1/2且 β = 1 \beta=1 β=1时,称为谱均衡滤波器。
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]
![]()