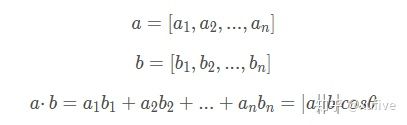numpy 点乘_细说NumPy数组的四种乘法，带你走进向量运算的奇妙世界

当孔乙己说回字有四样写法的时候，相信各位都是这样的表情吧？

但是，如果孔乙己说NumPy数组有四种乘法的时候，各位大约就是这样的表情了吧？

实际上，NumPy数组乘法远不止四种。为了在写作和阅读时保持清晰的逻辑和清醒的头脑，本文仅对四种最常见的数组乘法给出详细说明，并用一道数学题来演示向量点乘和叉乘的用法。

1. 星乘（*）

先声明一下：星乘这个说法，是我自己创造的，因为我实在不知道数组的这种乘法有没有其他高大上的名字，只好用运算符来表示了。所谓数组星乘，就是数组的对应元素相乘，这也是初学NumPy的同学最早接触到的数组乘法。

>>> import numpy as np
>>> a = np.array([1,2,3])
>>> b = np.array([4,5,6])
>>> a*b
array([ 4, 10, 18])

对于多维数组，星乘的规则也是一样。

>>> a = np.arange(6).reshape((2,3))
>>> b = np.arange(6,12).reshape((2,3))
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> b
array([[ 6,  7,  8],
       [ 9, 10, 11]])
>>> a*b
array([[ 0,  7, 16],
       [27, 40, 55]])

即使两个数组的shape不一样，只要满足特定条件，同样可以用星号相乘，且满足交换律。

>>> a = np.arange(6).reshape((2,3))
>>> b = np.array([1,2,3])
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> b
array([1, 2, 3])
>>> a*b
array([[ 0,  2,  6],
       [ 3,  8, 15]])
>>> b*a
array([[ 0,  2,  6],
       [ 3,  8, 15]])

2. 点乘（np.dot）

在数学上，向量点乘就是两个向量的对应位相乘后求和，因此向量点乘得到的是标量。

向量点乘的几何意义是两个向量的模之积再乘以二者夹角的余弦值。这意味着，如果两个向量互相垂直，则其点积为零。反过来说，两个不为零的向量的点积等于零，则两个向量垂直。

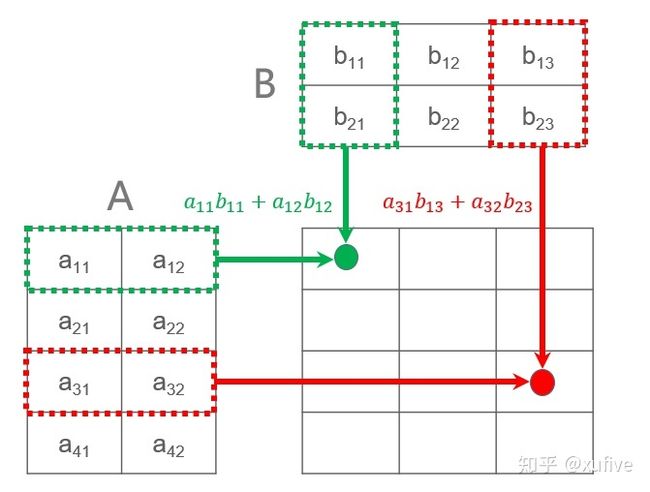
numpy.dot()函数提供了点乘运算。对于一维数组，NumPy的点乘就是向量点乘，其结果是一个标量。对于多维数组，则需要满足一定条件才能实现点乘，且其结果不再是标量，而是一个多维数组。比如，NumPy的矩阵相乘，就是二维数组的点乘，参与点乘的第一个数组的列数必须等于第二个数组的行数。

>>> a = np.array([1,0,0])
>>> b = np.array([0,1,0])
>>> np.dot(a,b) # 向量a和向量b相互垂直，其点积为0
0
>>> a = np.arange(6).reshape((2,3))
>>> b = np.arange(6,18).reshape((3,4))
>>> np.dot(a,b) # 满足点乘条件
array([[ 38,  41,  44,  47],
       [128, 140, 152, 164]])
>>> np.dot(b,a) # 不满足点乘条件
Traceback (most recent call last):
  File "", line 1, in 
    np.dot(b,a)
  File "<__array_function__ internals>", line 6, in dot
ValueError: shapes (3,4) and (2,3) not aligned: 4 (dim 1) != 2 (dim 0)

3. 叉乘（np.cross）

在百度和知乎上，有很多人说叉积就是外积，也有人提出不同意见。我在这里仅使用叉乘或叉积等确定无误的概念，以免误人子弟。在数学上，二维平面的向量叉乘，其结果是以两个向量为边的菱形的面积，三维空间的向量叉乘，其结果是仍然是一个向量，且垂直于相乘的两个向量，也就是参与相乘的两个向量决定的平面的法向量。nunpy.cross()函数可以实现向量（一维数组）叉乘，也可以实现二维或三维数组的叉乘。

>>> a = np.array([2,0])
>>> b = np.array([2,2])
>>> np.cross(a,b) # 平面向量叉乘，其结果是以两个向量为边的菱形的面积
array(4)
>>> a = np.array([1,0,0])
>>> b = np.array([0,1,0])
>>> np.cross(a,b) # x轴叉乘y轴，得到z轴
array([0, 0, 1])
>>> np.cross(b,a) # 叉乘交换顺序，得到反向的法向量
array([ 0,  0, -1])

4. 外乘（np.outer）

这里的外乘，类似于星乘，并不是通用的概念，也是我自己编造的一个说法，来源于numpy.outer()函数。从字面看，outer()函数更像是求外积，但从实际效果看，更像是笛卡尔直积，因此我这里用了“外乘”而不是“外积”。那么，outer()函数究竟能作什么呢？

>>> a = np.array([1,2,3])
>>> b = np.array([4,5,6,7])
>>> np.outer(a,b)
array([[ 4,  5,  6,  7],
       [ 8, 10, 12, 14],
       [12, 15, 18, 21]])

数组A外乘数组B，返回一个二维数组，这个二维数组的第i行是数组A的第i个元素星乘数组B。

5. 判断两条直线是否相交

假设abcd是欧氏空间中不重合的四个点，如何判断过点ab的直线和过点cd的直线是否相交？如果使用空间解析几何的方式来解决问题，对于一般程序员来说将是一个难题。不过，如果你熟悉NumPy，理解点积(np.dot)和叉积(np.cross)的话，解决这个问题就变得非常容易了。具体思路是这样的：

1. 计算向量ab和向量cd的叉积，得到向量orth
2. 如果orth的每一个元素都是零，则表示直线ab平行于直线cd，二者不可能相交；否则，orth就同时垂直于向量ab和向量cd
3. 计算向量orth和向量ac的点积，得到标量dp
4. 如果dp为零，表示向量orth垂直于向量ac，此时直线ab和直线cd在同一个平面上，且一定相交于某点

以上思路写成代码如下。

>>> def is_orthogonal(a, b, c, d):
	ab = np.array(b) - np.array(a)
	cd = np.array(d) - np.array(c)
	ac = np.array(c) - np.array(a)
	orth = np.cross(ab, cd)
	return orth.any() and np.dot(orth, ac) == 0