Leetcode 第 225 场周赛
Leetcode 第 225 场周赛
5661. 替换隐藏数字得到的最晚时间
给你一个字符串 time ,格式为 hh:mm(小时:分钟),其中某几位数字被隐藏(用 ? 表示)。
有效的时间为 00:00 到 23:59 之间的所有时间,包括 00:00 和 23:59 。
替换 time 中隐藏的数字,返回你可以得到的最晚有效时间。
示例 1:
输入:time = “2?:?0”
输出:“23:50”
解释:以数字 ‘2’ 开头的最晚一小时是 23 ,以 ‘0’ 结尾的最晚一分钟是 50 。
示例 2:
输入:time = “0?:3?”
输出:“09:39”
示例 3:
输入:time = “1?:22”
输出:“19:22”
提示:
-
time 的格式为 hh:mm
-
题目数据保证你可以由输入的字符串生成有效的时间
class Solution:
def maximumTime(self, time: str) -> str:
hour, minute = time.split(':')[0], time.split(':')[1]
hour1, hour2 = hour[0], hour[1]
minute1, minute2 = minute[0], minute[1]
if hour1 == '?' and hour2 == '?':
hour1 = '2'
hour2 = '3'
elif hour1 == '?':
if "0" <= hour2 <= "3":
hour1 = '2'
else:
hour1 = '1'
elif hour2 == '?':
if '0' <= hour1 <= '1':
hour2 = '9'
else:
hour2 = '3'
if minute1 == '?' and minute2 == '?':
minute1 = '5'
minute2 = '9'
elif minute1 == '?':
minute1 = '5'
elif minute2 == '?':
minute2 = '9'
time = hour1 + hour2 + ':' + minute1 + minute2
return time
5662. 满足三条件之一需改变的最少字符数
给你两个字符串 a 和 b ,二者均由小写字母组成。一步操作中,你可以将 a 或 b 中的 任一字符 改变为 任一小写字母 。
操作的最终目标是满足下列三个条件 之一 :
-
a 中的 每个字母 在字母表中 严格小于 b 中的 每个字母 。
-
b 中的 每个字母 在字母表中 严格小于 a 中的 每个字母 。
-
a 和 b 都 由 同一个 字母组成。
返回达成目标所需的 最少 操作数。
输入:a = “aba”, b = “caa”
输出:2
解释:满足每个条件的最佳方案分别是:
-
将 b 变为 “ccc”,2 次操作,满足 a 中的每个字母都小于 b 中的每个字母;
-
将 a 变为 “bbb” 并将 b 变为 “aaa”,3 次操作,满足 b 中的每个字母都小于 a 中的每个字母;
-
将 a 变为 “aaa” 并将 b 变为 “aaa”,2 次操作,满足 a 和 b 由同一个字母组成。
最佳的方案只需要 2 次操作(满足条件 1 或者条件 3)。
示例 2:
输入:a = “dabadd”, b = “cda”
输出:3
解释:满足条件 1 的最佳方案是将 b 变为 “eee” 。
提示:
- 1 <= a.length, b.length <= 105
- a 和 b 只由小写字母组成
思路:模拟
首先,目标是三个条件之一,我们需要分别考虑三种情况所需的最小操作次数,题目所求即为三种情况对应操作数的最小值。
- 对于第一种情况,我们实际上是要满足 a中的字典序最大字母比 b 中的字典序最小字母小。也即我们需要找到一个基准字母,使得 a
中所有字母小于等于该基准值,且 b 中所有字母大于该基准值(也可以定义基准为 aa 中所有字母小于,bb
中所有字母大于等于)。为达到这个目标,所需的最少操作数也就是 a,b 两个字符串中不满足该要求的字母数量,这需要我们提前维护 26
个字母桶记录 a, b 两个字符串中每个字母出现的个数。 - 为了找到“基准”字母,我们可以遍历 26 个字母,并分别计算得到以该字母为“基准”字母的最小操作数。
- 第二种情况和第一种情况同理。
- 对于第三种情况,我们只需找到一个“目标”字母,使得 a, ba,b
两个字符串中所有字母都变为该“目标”字母。为了达到这个目标,所需的最少操作数也就是 a, ba,b 两个字符串中不等于该字母的数量。
class Solution:
def minCharacters(self, a: str, b: str) -> int:
m = len(a)
n = len(b)
va = collections.defaultdict(int)
vb = collections.defaultdict(int)
for x in a:
va[ord(x)-ord('a')] += 1
for x in b:
vb[ord(x)-ord('a')] += 1
# a中小于等于基准,b中大于基准
case1 = m + n
for i in range(25):
cur = 0
for j in range(i+1,26):
cur += va[j]
for j in range(i+1):
cur += vb[j]
case1 = min(case1, cur)
# b中小于等于基准,a中大于基准
case2 = m + n
for i in range(25):
cur = 0
for j in range(i+1,26):
cur += vb[j]
for j in range(i+1):
cur += va[j]
case2 = min(case2, cur)
case3 = m+n
for i in range(26):
cur = 0
for j in range(26):
if i == j:
continue
cur += (va[j]+vb[j])
case3 = min(case3, cur)
return min(case1, case2, case3)
复杂度分析:
-
时间复杂度为 O(n),遍历了字符串。
-
空间复杂度为 O(n),利用了两个桶记录两个字符串不同字母的数量。
5663. 找出第 K 大的异或坐标值
给你一个二维矩阵 matrix 和一个整数 k ,矩阵大小为 m x n 由非负整数组成。
矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j](下标从 0 开始计数)执行异或运算得到。
请你找出 matrix 的所有坐标中第 k 大的值(k 的值从 1 开始计数)。
示例 1:
输入:matrix = [[5,2],[1,6]], k = 1
输出:7
解释:坐标 (0,1) 的值是 5 XOR 2 = 7 ,为最大的值。
示例 2:
输入:matrix = [[5,2],[1,6]], k = 2
输出:5
解释:坐标 (0,0) 的值是 5 = 5 ,为第 2 大的值。
示例 3:
输入:matrix = [[5,2],[1,6]], k = 3
输出:4
解释:坐标 (1,0) 的值是 5 XOR 1 = 4 ,为第 3 大的值。
示例 4:
输入:matrix = [[5,2],[1,6]], k = 4
输出:0
解释:坐标 (1,1) 的值是 5 XOR 2 XOR 1 XOR 6 = 0 ,为第 4 大的值。
思路:前缀和
这道题的思路大家基本都能想到,就是计算出二维矩阵matrix中每个元素的大小,然后经过排序找到第K大的值。但是由于数据范围非常大,如何在O(m*n)的时间复杂度下计算出整个matrix数组中的所有元素值成为了这道题的考点。
我们可以发现,对于我们要计算的m[i][j]这个元素的值是满足这个公式的:
m[i][j]=m[i−1][j−1]⊕m[i][j−1]⊕m[i−1][j]⊕m0[i][j]
其中m0表示原矩阵的数值,m表示计算后得到的值。满足这个公式的原因可以用这个图解释:
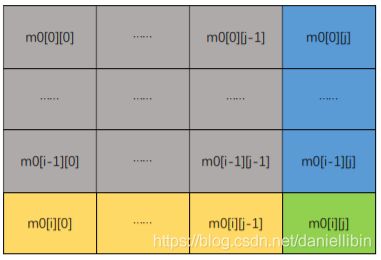
其中m[i-1][j-1]是图中全部灰色部分的异或结果,m[i][j−1]是图中全部灰色部分与黄色部分的异或结果,m[i-1][j]是图中全部灰色部分与蓝色部分的异或结果。所以根据异或的性质,
m[i][j−1]⊕m[i−1][j]的结果是黄色部分与蓝色部分的异或结果,而将
m[i-1][j-1]⊕m[i][j-1]⊕m[i-1][j]⊕m0[i][j]就组合成了整个图中所有元素的异或结果。
通过以上方法计算出m的所有元素后,对他们进行排序,取到第k大的元素即可。
Code1:
class Solution:
def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
m = len(matrix)
n = len(matrix[0])
res = []
res.append(matrix[0][0])
for i in range(1,m):
matrix[i][0] = matrix[i-1][0] ^ matrix[i][0]
res.append(matrix[i][0])
for j in range(1,n):
matrix[0][j] = matrix[0][j-1] ^ matrix[0][j]
res.append(matrix[0][j])
for i in range(1,m):
for j in range(1,n):
matrix[i][j] = matrix[i-1][j-1] ^ matrix[i][j-1] ^ matrix[i-1][j] ^ matrix[i][j]
res.append(matrix[i][j])
res.sort(reverse = True)
return res[k-1]
复杂度分析:
-
时间复杂度:O(mnlog(mn))
-
空间复杂度:O(m+n)
Code2(使用堆):
class Solution:
def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
m = len(matrix)
n = len(matrix[0])
heap = []
heapq.heapify(heap)
heapq.heappush(heap, matrix[0][0])
for i in range(1,m):
matrix[i][0] = matrix[i-1][0] ^ matrix[i][0]
if len(heap) < k:
heapq.heappush(heap, matrix[i][0])
else:
if heap[0] < matrix[i][0]:
heapq.heappop(heap)
heapq.heappush(heap, matrix[i][0])
for j in range(1,n):
matrix[0][j] = matrix[0][j-1] ^ matrix[0][j]
if len(heap) < k:
heapq.heappush(heap, matrix[0][j])
else:
if heap[0] < matrix[0][j]:
heapq.heappop(heap)
heapq.heappush(heap, matrix[0][j])
for i in range(1,m):
for j in range(1,n):
matrix[i][j] = matrix[i-1][j-1] ^ matrix[i][j-1] ^ matrix[i-1][j] ^ matrix[i][j]
if len(heap) < k:
heapq.heappush(heap, matrix[i][j])
else:
if heap[0] < matrix[i][j]:
heapq.heappop(heap)
heapq.heappush(heap, matrix[i][j])
return heap[0]
复杂度分析:
- 时间复杂度:O(mnlog(k))
- 空间复杂度:O(k)