多编程范型下的函数式编程（上篇）——基本概念

引言

        我们接触较多的主要是过程型编程（C语言）、面向对象编程（Java语言）和泛型编程（C++ Template），每种编程范型都有自己的优缺点，在软件开发实践中往往不会只用一种编程范型。比如，过程型编程符合冯诺依曼体系结构的计算机，便于编译和执行，因此执行效率较高，适合系统级编程；面向对象编程符合对客观世界的建模，因此是业务系统的不二选择；泛型型编程有利于构造类型无关的通用模板，增强代码复用性。

        然而，这些编程范型在应用上也是有联系的，面向对象中方法里通常使用过程型编程实现，而对象的类型可以利用泛型技术达到更强的复用性和类型安全。我们日常的软件开发无法离开这些范型，只支持一种范型的编程语言是没用生命力的（比如C语言和PHP，C语言还坚挺只是因为所有的操作系统都是由C构造，至于PHP，呵呵呵呵）。

        函数式编程思想和实践是我们较少接触的，但函数式编程是一种历史比较久的编程范型。由于其无状态特性、无副作用的特性，在分布式和并发程序设计中优势明显，因此在最近一些年中越来越流行起来，在主流的编程语言，如Java、C++、Python、Javascript的较新版本中都加入了函数式编程的支持。同样，函数式编程也有缺点，我们不可能只使用函数式编程完成所有软件开发。因此，混合函数式编程思想和技术的多范型编程更加合理。

        本系列文章主要以函数式编程为重点，讨论其基本概念、应用和原理理论。同时在讨论这些函数式编程论题时与其他编程范型结合，考察函数式编程如何与其他编程范型结合，一来利于读者接受和理解相关函数式编程论题，二来利于读者在进行混合范型编程时能够正确合适的使用函数式编程的特性。

        本系列文章分为三篇文章：

•    上篇：基本概念，即讨论函数式编程的基本概念和基本应用，以及和其他编程范型的联系
•    中篇：应用，即把函数式编程放到广泛的业务场景中，考察其有哪些应用模式、惯用法、框架和工具，如何与其他编程范型配合，以及有哪些需要注意的地方
•    下篇：原理与理论，即向下深入挖掘函数式编程的理论模型，研究函数式编程语言在编译和运行期间的主要工程技术

函数

        在过程型语言中最重要的语言要素是变量，在面向对象语言中最重要的则是对象，而在函数式语言中最重要的就是函数了。变量、对象和函数都是各自编程范型中的头等程序对象，都可以当成参数、返回值进行传递，以及进行赋值和应用等操作。

        我们对于函数比较陌生，难以想象函数如何像面向对象语言中的对象那样无所不能。那么下面将非形式化的尝试将函数和对象建立一种类比映射关系，帮助大家理解。

函数和对象的类比

        注：本节论述的代码采用类似Java的伪代码，相信你一看就懂。

        首先定义两个函数，非常简单的加法（add）和减法（subtract）函数：

int add(int a, int b){

     return a+b;

}

int subtract(int a, int b){

     return a-b;

}

        虽然这两个函数语义完全不同，但是他们有着相同的参数和返回值类型，因此我们认为这两个函数是同一函数类型，类型为(int, int) => int，意为两个int参数返回一个int值。

        然后我们再来定义两个对象userA和userB：

User userA=new User(“mikes”);

User userB=new User(“john”);

         userA和userB这两个对象（或者对象的引用，这里不做区别）代表不同的用户，但是这两个对象也是同一类型，类型为User。

         说到这儿是不是感觉函数和对象神似呢？还没完，接着看。

        在面向对象范型语言中，我们可以将已有对象赋值给其他User类型的对象引用，就像别名：

User userC=userB;     //userC和userB是同一对象，你也可以认为userC是userB的别名

        函数式范型语言中的函数实际上也可以这样进行赋值：

(int, int) => int addRef = add;   // addRef和add函数是一样的

        是不是感觉(int, int) => int类型太长了呢？我们可以定义函数的类型名：

type TwoMapOne (int, int) => int;

        我们还可以和泛型配合使用：

type TwoMapOne (T, T) => T;

        这样上面的赋值语句变为TwoMapOne addRef=add;

        对象有时候是匿名的，比如：return new User(); 并没有对象引用的名称；与之类似，函数也可以是匿名的，比如(int a, int b) => int { return a*b}，通常匿名函数称之为lambda函数。现代编译器足够智能，可以根据类型推测让你少写很多代码，比如上面的lambda可以简写：

TwoMapOne functionD = (a, b)=> a*b;  // 因为左侧TwoMapOne已经限定了类型，右侧的lambda函数不必写全所有的类型名int。

        函数应用就是函数的调用，就像对象的调用一样，比如：

userA.setName(“mikes”);  // 操作对象行为，改变对象状态，是对象的应用

int result = add(3, 5);  // 对函数的实际调用，是函数的应用

        综上，我们把函数和大家熟悉的面向对象中的对象建立了概念上的一一映射，这样一来我们完全可以把函数当成头等程序对象，对象能干什么，函数就能干什么，比如当成参数传递，作为返回值返回，函数内部再创建函数等等。

        然而，事情并没有你想的那么简单，函数式编程还是有它自身的技术特点，毕竟函数和对象是分别隶属两种不同编程范型的概念，遵循不同的设计思想，上文的类比只是从表象上进行了联系，便于大家快速理解函数。

函数和对象的差异性

状态可变性

        首先，对象是对现实世界中实体的抽象，现实世界的实体大多是有状态的，因此对象也大多是有状态的。比如Java码农经常编写的各种Java Bean，调用一次setter方法，对象的状态实际上就改变了。

        而函数则提倡无状态性。函数的无状态体现在输入输出上：任意给定一组参数，无论何时调用函数，传递这组参数，都能得到相同的返回值。

        实际上，后文提到的闭包会让函数变得有状态，但是至少函数式范型提倡无状态编程。

副作用

        所谓副作用通俗的讲是函数可以通过自己的执行对函数外部产生“影响”，而非仅仅通过返回值“影响”外部。比如，print函数，它并不返回任何值，而是将参数打印到屏幕上，这就是函数的副作用。

        在函数式范型中，提倡无副作用的函数，因为副作用范围太大了，无法预知，容易出错。而在面向对象范型中，我们常常看到各种void类型的方法，因为对象调用这些方法改变自身状态本身就是副作用。因此，状态和副作用是相辅相成的。

方法和函数的关系

        面向对象范型中的对象方法和函数式范型中的函数是一回事么？对于这个问题，可能大多数读者给出的答案是肯定的，或者说下意识的认为是肯定的。但是很遗憾，方法和函数不是一回事，不过欣慰的是它们有联系，方法是函数的一种。

        下面是User类中getName方法的定义：

class User {

       privateString name;

       publicString getName() {     return name;     }

}

        既然方法是函数的一种，那么getName方法也应该有函数类型，它的函数类型是User => String。

        也许你会问，明明getName没有参数，为什么它的类型不是() => String呢？实际上，它的参数就是引用getName的对象。我们不妨假设getName的类型是() => String，由于函数可以赋值，我们做如下赋值：

() => String func = someUser.getName;

        这样当我们应用func函数时，就不明白func返回的究竟是哪个对象的name呢？而且更为重要的是当我们调用func()函数两次时，如果someUser对象的状态被改变，那么func()函数将返回不同的值，这就进一步的增加了困惑。

        因此，面向对象中类的成员方法是以该类为第一个参数类型的函数。

        弄明白了成员方法和函数的关系，我们便容易得出类的构造方法和函数的关系：

类的构造方法是以该类为返回值类型的函数。

偏应用函数

        偏应用函数（Partial Applied Function）：对于具有多个参数的函数，调用时只传一部分参数，这时返回值将是一个新函数，新函数以原函数剩余的参数为参数。这个返回的新函数称为原函数的偏应用函数。

        以伪代码举个栗子，调用上一章创建的add函数，add(3, 5)会返回一个整数8；但是如果调用add(3)返回的就不是一个整数了，而是一个新的函数，这个函数的类型是int => int，进一步lambda表达式为b => 3+b。add(3)就是把函数中得a赋值为3，然后把剩下的部分作为新的函数返回。

        当然，我们也可以对函数的第二个参数进行偏应用：add(_, 5)，这时返回的函数是a => a+5。

        我们可以利用这种机制灵活的构造新的函数。

        上述示例是以伪代码说明，实际上大部分支持函数式编程的语言都支持偏应用函数。

        在Python中，functools.partial函数被用来创建偏应用函数。比如int函数有两个参数，value和base，int函数作用是以base为底，将value转换成相应数值。我们可以创建新的以2为底的数值转换函数int2：

int2 = functools.partial(int, base = 2)

        int2就是int的偏应用函数。

        在Scala中，创建偏应用函数更加简单，以int函数为例，int2函数：

int2 = int(_, 2)

        直接传递应用的参数，不应用的参数用_代替。

柯里化

        首先隆重介绍一下计算机系屌丝应该膜拜的一位前辈Haskell Brooks Curry（柯里1900-1982），柯里是一位很牛逼的数学家和逻辑学家，他为计算机领域做出了很多贡献，最为人熟知的就是发明了函数式语言Haskell。本文介绍的两个概念和柯里有关：currying函数和函数的currying（柯里化函数和函数柯里化）。

柯里化函数

        简单学习过函数式编程的人可能听说过currying函数。首先，currying函数是一种函数，这种函数拥有多个参数列表，每个参数列表只有一个参数。

        举例说明，刚才的add函数的参数列表只有一个add(int a, int b)，而这个参数列表由两个参数组成（int a和int b）。相应的currying函数为：add_currying(int a)(int b)，它带有两个参数列表，每个参数列表只有一个参数。要完成一个完整的函数调用则为：add_currying(3)(5)，结果将返回8，这和调用add(3, 5)结果是一样的。

        如果add_currying函数只是传递了一个参数，则返回另一个函数，这个函数仍然带有一个参数的参数列表。比如add_currying(3)返回b->3+b这个函数。这和add函数传递一个参数的效果也是一样的。

        从上述实例中，我们看不出非柯里化函数add和相应的柯里化函数add_currying除了参数列表外有什么实质区别。

这种理解方式比较表面化，没有揭示currying函数的本质，如果只是这样理解的话，实际上无法解释currying函数和上文介绍的偏应用函数的区别。

        关键在于add和add_currying的类型不同！

        add函数的类型是(int, int)=> int，这很容易理解，两个int型参数返回一个int型结果；

        add_currying函数的类型则是int => (int=> int)，理解为以一个int型参数返回一个函数，这个函数以第二个int型为参数，返回int型结果。

       看出区别了么？currying函数和偏应用函数看起来很像，其实函数类型是完全不一样的。

       由此，我们可以这样非形式化的描述currying函数：

A：currying函数只有一个参数；

B：currying函数的返回结果要么是另一个currying函数，要么是一个实际值。

       这显然是一个隐含着递归的定义，例如三个参数列表的currying函数add_three_currying，它的函数类型是int => (int => (int => int))，至于具有4个、5个，甚至更多个参数列表的currying函数，其函数类型以此类推应该能很快写出。

        理论上讲，currying函数的效率和开销要比普通函数要大，比如，Add_currying(3)(5)实际上调用了两个函数才算出8这个结果。但是现代函数式语言编译器往往做了诸如惰性求值等优化，因此性能方面还行。

        currying函数和偏应用函数从使用角度还有一个重要区别，普通函数偏应用可以针对任何参数，但是currying函数在应用的时候只能从第一个参数开始，然后是第二个，依照顺序进行。

        总的来讲，各种函数式编程语言的趋势是屏蔽currying函数和偏应用函数在内部机制上的区别，为用户提供简单一致的编程体验， 并提供转换机制方便的将普通函数转换成相应的currying函数。

        最后再啰嗦一下：既然偏应用函数在使用上和currying函数差不多，而且功能貌似还更强大，那么currying函数有何价值呢？其实currying函数这个概念从上世纪六七十年代就有了，从理论角度，单参数函数对一些理论更容易研究和讨论，在编译理论方面，单参数函数也有更多的优化方案，具体不再展开，有兴趣的话可以参考https://en.wikipedia.org/wiki/Currying#Mathematical_view

函数柯里化

        如果说柯里化函数是一个函数，那么函数柯里化则是一个过程，这个过程将普通函数变成一个柯里化函数。

        对于现代函数式语言，如Haskell和Scala，都支持函数柯里化。比如我们定义一个三个参数的普通函数sample：

int sample(int a, int b, int c){…….}

        sample的类型为(int, int , int)=> int，我们可以容易的获得其相应的柯里化函数：

var sample_currying = sample.currying;

        变量sample_currying是柯里化函数，类型为int => (int => (int => int))。

        实际上，在Haskell语言中，所有的函数在编译后都变成了柯里化函数，所有函数的类型都是相应柯里化函数的类型。也就是说，sample函数的类型直接就是int => (int => (int => int))。

        看来，如果不理解柯里化函数就直接学习Haskell语言的话，一定会纠结我们定义的函数怎么会是这种类型。

        相比之下，Scala语言就厚道了许多，虽然它也支持显式的柯里化操作，但是它在日常编程中尽量为我们屏蔽柯里化过程。（然而这也并不能改变Scala成为仅次于C++的第二复杂的编译型语言）

闭包

        闭包（closure）：具有自由变量的函数，在运行时完成自由变量绑定后的称谓。所谓自由变量，指的是在函数外部定义的非全局变量。

       下面是一个简单的函数定义：

void outer(){

    int offset = 0;

    int inner(intarg){

              int a=1001;

              int b=2002;

              return arg + a + b + offset;

    }

}

        offset并没有在inner函数定义，在函数式语言中，像offset这样的变量称之为自由变量；而a和b在函数内部定义的变量，以及函数参数arg称为约束变量。

        在编译期，编译器会在inner的上下文寻找offset的定义，如果找不到，就升高一层上下文继续寻找（比如inner函数定义在某个函数的函数中），直到找到为止。

        但是在编译期并不知道offset的实际值或者在内存中的实际地址，这些信息是运行时信息。因此，inner中的offset变量要在运行期和其上下文的offset定义完成绑定。

        绑定完成后，我们将inner函数和绑定后的offset变量成为闭包。

        具有自由变量的函数定义在编译期称为open term（term代表一块代码，就是开放的、不确定的一块代码）。

        不具有自由变量的函数定义在编译期称为closed term。没有自由变量的函数定义在运行时不能称谓闭包，因为它在编译期的所有变量绑定就已经确定了（closed）。

        在上述代码中，inner函数既可以是闭包（closure），也可以称为open term，具体称谓取决于运行期还是编译期。闭包和open term属于同一个函数不能让我们很好的理解这些概念的深刻含义，下面一段Python代码展示闭包和open term分别属于不同函数的例子：

def f(x):

   def g(y):

        return x + y

return g

a = f(1)

b = f(10)

        上述共有四个函数，f、g、a、b，其中f是高阶函数，即f的返回值是另一个函数g，函数g的内部有一个自由变量x，即函数f的参数。

        四个函数中，a和b函数是闭包（closure），g函数是open term，f函数是closed term。a函数是在x=1时的g函数，而b函数是在x=10时的g函数，a和b函数都是在运行时，g的自由变量绑定值之后的称谓。

        闭包是一个经常被误解的概念，要正确的认识闭包，我们必须区分编译期和运行期，闭包是运行期函数和自由变量完成绑定时的称谓。不过，在具体应用时，为了叙述方便并且不会产生歧义的前提下，我们也可以不加区分的把closure和open term统称为闭包。

        闭包中的自由变量绑定是按名绑定的，所谓按名绑定就是说在上述代码中，g函数中的x变量和f函数的参数x是同一个变量。

        与按名绑定相似的概念是按引用绑定和按值绑定。简单介绍一下后两者：

        如果是按引用绑定，则g函数的x变量和f函数的参数x将是不同的变量，但是这两个x变量初始引用的将是同一个对象。

        如果是按值绑定，则g函数的x变量和f函数的参数x也是不同的变量，而且两个x变量初始引用的对象也不一样，但是两个x各自引用的对象数值上是相同的，即互为拷贝关系。

        对于闭包中的自由变量是按名绑定，有的语言支持在闭包中修改自由变量，有的语言则不允许（比如Java中不允许修改匿名类的方法中使用的外部变量）。

       本节澄清了闭包的理解。但不得不说的是，闭包是一个存在很久的定义。如果在未来，编程语言技术和编译器技术足够强大到让函数的自由变量在编译期完成绑定，那么那时我们也许就可以简单的认为闭包就是具有自由变量的函数了。

       最后在抛出一个问题，既然本文的题目是多范型下的函数式编程，那么我们就不能忘了其他编程范型。在面向对象语言，比如Java中，对象的成员方法内常常访问对象的成员变量，比如User的getName方法：

class User {

       privateString name;

       publicString getName() {

              returnname;

       }

}

        getName方法中的name变量并没有在getName内部定义，那么是不是可以说在运行时getName方法也是闭包呢？

        答案是否定的！

        在上文我们探讨过，从函数角度看，getName方法是有参数的，getName的参数就是User对象，而name是参数的内部成员。getName方法等价于如下函数定义：

String getName(User user){

       returnuser.name;

}

        也就是说，name是getName函数的约束变量，并不是自由变量，因此不是闭包！

Monoid

        Monoid翻译为幺半群，即带有独异点的半群，是抽象代数里的一个重要代数结构。But what fucking these？先别急着抓狂，先看一个码农喜闻乐见的东西。

        码农喜欢新鲜事务，在Java 8中为Collection接口引入了许多新方法和机制，其中就有新增的Stream。Stream接口和Collection接口的关系详见Java参考书，重点要说的是Stream接口的一个名为reduce的方法。

Optionreduce(BinaryOperator operator);

        reduce操作将集合的所有元素每两个一组应用operator操作，再将结果再两两一组应用operator操作，直到最终得出一个值，如果只有一个值则直接返回这个值。operator是一个二元操作，即需要两个参数操作数。

        举个栗子：假设集合中有4个元素（3，4，5，6），operator为lambda：(a, b) -> a+b，即普通的加法运算，那么reduce操作为((3+4)+5)+6，结果为18。

        但是坑来了：Java 8 API里有这么句话，大意是由于Stream的操作是支持多线程并行优化的，reduce操作不保证集合中二元操作的顺序。也就是上面的执行还可能是(3+4)+(5+6)，即用于并行计算的二路归并计算顺序，不过计算结果是一样的，也是18.

        看到坑点了么？没错，你必须保证传入的operator函数符合结合律！如果operator是(a, b) -> a-b就坏了，因为(a-b)-c != a-(b-c)，最终的结果可能不是你想要的。

        reduce还有一个重载版本：T reduce(Tidentity, BinaryOperator operator)

也就是预先将结果设置为identity，这样就不需要判断集合是否为空，或集合是否只有一个元素的情况了，reduce的实现代码大体如下：

    T result = identity;

    for (T element : this stream)

        result = operator.apply(result, element)

    return result;

        在上面的实现中没有一个if判断语句，而且返回值类型也不再是Option，而是T，因为即使集合为空，也一定会返回具体值（即identity）。因此这个重载版本的reduce在并行优化时无需加锁，性能更好。

        那么问题来了，identity传什么值呢？Java 8 API要求传入的identity满足条件：对于集合中得任意元素x，operator(identity, x) = x成立。

        那么，对于加法运算，identity只能是0了。

        也许有人会自作聪明：identity随便传一个值，最后再减去不就得了？比如identity传1，然后调用的时候做如下处理：

int result = stream.reduce(1, (a, b) ->a+b)-1;

        如果是单线程串行操作，没有问题；但是如果reduce内部开启了多线程优化，问题就来了，比如开启了两个并发线程，对集合(3,4,5,6)运算可能是这样的：

1+(1+3+4)+(1+5+6)

        identity被使用了不止一次哟，最后只减去一个identity能行么？

        所以，传递identity参数时还是按照Java 8 API要求来吧。

        好了，现在回过头来讨论monoid，monoid这个概念在抽象代数中的定义如下：

        monoid由一个集合S和一个二元运算符.构成的代数结构，满足如下：

1、对于S内的任意元素a,b,c，(a.b).c=a.(b.c)成立

2、S内存在一个元素e，对于S内的任意元素a，a.e=e.a=a成立

        看出和Stream.reduce方法的联系了吧，stream集合，identity参数和operator参数共同构成了一个monoid！。

        各种支持函数式编程的语言普遍支持reduce函数。然而在python和haskell中的reduce函数被称为fold函数，但其实是一个东西，不要搞不清楚喔。

Functor和Monad

（注意！前方高能！）

        终于要进入函数式编程最装逼的概念了，没错，就是Functor和Monad。由于函数式编程在中国的码农中还不是特别普及，使用过这两个东东的就更少了，所以至今没有合适的中文翻译。有人将Functor翻译为函子，Monad翻译为单子，但是貌似没有任何官方说法认同。

类型的包装

        Functor和Monad都是对已有类型的包装。

        假设一种同时支持面向对象和函数式编程的语言，比如Scala，把它的所有对象类型和函数类型放在一个类型系统T中，所谓类型系统可以简单的看成一个类型集合，集合中有两种元素：

1、        对象类型，比如Integer、String、以及我们的自定义类型

2、        函数类型，包括所有的单参数函数类型、双参数函数类型、三参数函数类型，以及N个参数的函数类型

        注意，这里我们不区分函数类型中的参数和返回值类型，比如String => String和Integer => Integer这两个函数类型我们认为是同一个函数类型，都是单参数函数，不区分参数和返回值的具体类型。

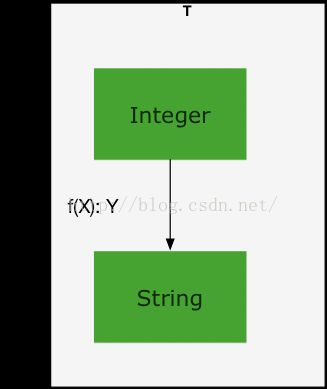
        用图形方式展示，集合T如下：

        我们用绿色方框表示集合中的类型，如Integer和String；用箭头线表示函数类型，图中只画了一个单参数函数，因为之前约定不区分函数的参数和返回值类型，因此参数和返回值分别用X和Y表示。

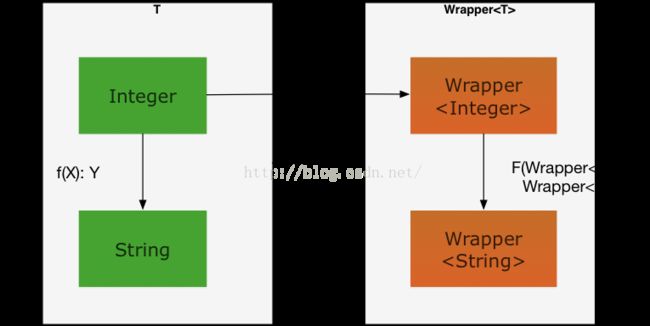
        现在有这样一种需求，我们要为T集合中的所有类型添加某种功能。为此，我们借鉴泛型编程的理念，创建一个Wrapper泛型类型。由于Wrapper类型是对T类型的增强，我们希望在应用中只使用Wrapper类型，而不使用T类型，比如，我们希望用Wrapper类型替换掉String类型。

        Wrapper形成新的类型集合如下：

        在新的类型系统中，我们有了新的类型Wrapper，Wrapper，以及之前的单参数函数f在新集合变成了新的单参数函数F：Wrapper => Wrapper，在这个新类型系统中，所有的类型都加上了Wrapper包装。

        我们要让Wrapper类型替换掉T类型，我们必须解决如下两个问题：

1、        给定一个T类型的对象，如何构造Wrapper类型的对象呢？

2、        给定一个单参数函数，比如String toString(Integer)，如何得到在新类型系统下得对应函数呢？即WrapperwToString(Wrapper)

        对于第一个问题，码农的第一反应就是构造函数。没错，如果认为Wrapper是一个泛型类的话，只需要提供一个Wrapper(T element)构造函数，就解决了第一个问题。

        对于第二个问题，我们提供了一个函数映射值，为什么不能提供一个函数映射函数呢？没错，我们需要提供一个map函数，map函数接受一个T集合中的单参数函数，返回值也是一个函数，即新系统下的函数。map函数是一个高阶函数，其类型是(X => Y) => (Wrapper => Wrapper)。有了map函数，我们就很容易解决第二个问题了：wToString = map(toString)

        解决了这两个问题，我们就把T集合和Wrapper集合初步的建立了联系：

        好了，讨论到这里就可以首先揭开Functor的神秘面纱了。Wrapper是一个单类型参数的泛型类型，如果Wrapper实现了上面的两个函数Wrapper构造函数和map函数，那么我们将这样的泛型类型称为Functor。

        是不是突然觉得Functor异常的简单，只不过是实现了两个特定方法的泛型类而已嘛。但是为什么在Java和C++从来没有这样的概念呢？问题的答案就在map函数上，刚才说了，map函数的参数和返回值都是函数，也就是说map是高阶函数，但是Java和C++长久以来都不是支持函数式编程的语言，因此根本不支持编写像map这样的高阶函数，当然也就没有Functor这个概念了。

        然而在最新的Java 8和C++ 11中，引入了lambda，开始支持函数式编程，使得map之类的高阶函数得以支持，Functor这个在函数式编程中重要的概念就被Java和C++引用和重新提出了。在Java 8中有一个Optional类，这个类实际上就是个Functor，这个类的作用也很简单，就是为了防止Java中的空指针异常，这个类后面还会讨论，现在先按住不表。

        Functor介绍完了，再来讨论一下什么是Monad。

        Wrapper这个包装类中包装的是T集合中的类型，我们能否扩展一下，让Wrapper包装的类型也可以是Wrapper类型呢？也就是支持Wrapper>，即泛型嵌套类型。

        如果我们支持泛型嵌套类型，从逻辑上讲，Wrapper>相当于T的两次包装，当然也可以出现T的三次封装甚至四次封装。这时，你会想到这样的类型在实际使用的时候好麻烦呐，我们能不能提供一个函数，不管是对T的多少次封装，反正都是封装，这个函数返回的是T的一次封装就好。这个函数定义如下：

Wrapperjoin(Wrapper> wrapper)

        Join函数接受一个T类型对象的二次封装对象，返回一个简单的一次封装对象。直观感觉上，这是不是有点类似于降维。

        好了，这下可以引入Monad了。所谓Monad就是一个Functor，这个Functor支持嵌套的泛型封装，并且提供join函数用来降维。也就是说，Monad是加上更多条件的Functor。

        说到这里，还记得我们为什么提出构建Wrapper类型么？对了，我们的目的是让功能更加丰富的Wrapper替换掉T类型。但是前面的论述有个问题不知道大家发现了没有。

        map函数将T类型的单参数函数转换成Wrapper类型下的单参数函数，但是T类型下的双参数函数怎么办？三个参数的函数怎么办？我们在编程的时候可不是只写一个参数的函数哦。如果这个问题不解决，我们就没法让Wrapper替换掉String类型，毕竟任何一种语言对String类型都有一堆函数，而这些函数可不是只有一个参数。难道我们还必须自己编写map2函数，map3函数解决这个问题么？

        我们需要map2函数和map3函数，但是令人欣慰的是，我们不需要自己编写，这些函数可以自动生成。首先考察两个参数的情况，有如下引理支持，非严格的描述如下：

       引理：如果Wrapper类型是Monad，给定T类型下的双参数函数f2:(X, Y) => Z，则f2函数在Wrapper类型下得对应函数F2: (Wrapper, Wrapper) => Wrapper可以利用map、join和Wrapper构造函数在有限次步骤内得到。

        这个引理的证明过程详见附录A。

        既然我们利用仅有的三个函数构造出了map2，那么我们能否构造出map3、map4、甚至mapN呢？答案是肯定的，并且我们有如下定理支持：

        定理：如果Wrapper类型是Monad，给定T类型下的多参数函数fn，则fn函数在Wrapper类型下得对应函数Fn可以利用map、join和Wrapper构造函数在有限次步骤内得到。

        这里不再证明这个定理，大家感兴趣的话可以仿照引理的证明过程，利用数学归纳法证明，也不是很复杂。

        这个定理意味着什么？意味着我们只需要提供Wrapper三个函数，就可以让编译器自动为我们生成T类型下所有函数在Wrapper里对应的函数。由此，我们完全可以用Wrapper类型替换掉T类型了。

        最后解释一个问题，Wrapper是否应该提供一个get函数，在获取对应的T类型对象？这个get函数相当于Wrapper构造函数的一个逆函数，这个get函数是非必须的，如果你需要，就可以提供，不提供也无所谓。因为之前已经说过，我们的目的是用Wrapper类型替换掉T类型，既然已经替换掉了，干嘛还要返回T类型对象呢？

        下面以一个Java 8中的Monad Optional结束本节。

Java 8的Monad实例

        Optional是Java 8中新增加的一个泛型类，你可以认为Optional就是刚才我们讨论的Wrapper类型的一个例子，因为它确实是个Monad。

        Optional的作用很简单，就是防止空指针异常。之前我们的Java方法可能返回null，比如：

User user=Factory.getUser();

        如果user是null，则接下来调用user时会抛出空指针异常。我们可以修改一下getUser方法，让其返回Optional

Optional optional =Factory.getUser();

        这意味着optional一定不会是null，你可以通过optional.isPresent()判断Optional包装的User对象是不是null。

        接下来，假设Factory类有一个静态方法User handle(User user)方法，假设optional里的User不是null，那么我们可以通过optional.get方法获取到User对象，然后把它传给handle方法做后续处理。

        上面介绍的关于Optional类的用法你在百度里能找到一堆类似的介绍，甚至在Java 8的官方文档也是这么介绍的。但是通过本章对Functor和Monad的深入探讨，我们对Optional的理解应该超越这些介绍。

        我们说Wrapper可以替换掉T，Optional就是Wrapper，我们也能用Optional彻底替换User。但是我们现在只有handle(User user)方法，我们需要的是handle(Optional optional)方法，经过上面的讨论我们已经知道，这个新的handle方法根本不需要我们重新写，利用map方法就能搞定，修改后的代码如下：

Optional optional =Factory.getUser();

Optional updated = optional.map(factory::handle);

        我们只用了两行代码，中间没有任何判断User对象的代码，也没有把User对象取出来，User的包装类Optional替代了User类！

        那要是两个参数的方法呢？比如handle(User userA, User userB)。通过上面的讨论，我们知道理论上编译器是能够为我们自动生成Optional的相应方法handle(Optional opA, Optional opB)。但是很遗憾，理论归理论，Java还是走在了理论的后面，Java8编译器并不能提供这样的自动生成支持，我们不得不自己实现，要么就简单的把userA和userB对象都取出来，然后调用原handle方法。

        反观其他函数式语言，比如Haskell和Scala，虽然也没有直接自动生成包装类型的handle方法，但是这些语言提供了语法支持，能够让你很方便的编写handle(Optional opA, Optional opB)。所以Java 8在函数式编程的支持上其实还有很多路要走。

小结

        本节用了较大的篇幅介绍了函数式编程最难的Functor和Monad概念，这两个概念难就难在它的理论基础是一般计算机专业都不曾学过的范畴论。实际上，在上文论述中提到的T类型和Wrapper类型是范畴论中的两个范畴，而map函数、Wrapper构造函数在范畴论中得术语叫做态射。论述的时候有意避开了这些无关紧要的术语，如果你想继续深入学习的话可以研究一下范畴论。

        虽然Functor和Monad是函数式编程概念，但是在本节的讨论中并没有离开其他编程范型的支持。Functor和Monad在实现的时候就是两个泛型类型，而实际的类型就是面向对象中的类。通过泛型编程和面向对象编程的支持，Functor和Monad实现起来简单而易懂。感兴趣的话可以看下Haskell中的Functor和Monad，由于Haskell是纯函数式语言，既不支持面向对象编程，也不支持泛型编程，导致其Functor和Monad的实现和应用十分晦涩；然后在对比一下Scala和Java 8中的Functor和Monad，你就会感受到多范型编程的魅力。

模式匹配

        提起模式匹配往往让人联想到正则表达式之类的东东，但是函数式编程中的模式匹配真心不是指的这些。

        用过C、C++或者Java的人都应该接触过Switch-case语句，简单的说，你可以理解为模式匹配是增强版的switch-case。需要指出的是，这里的增强不是增强一点半点，而是增强很多很多，甚至大有替换if-else之势。

        下面论述四个模式匹配的主要特性，至于简单的单变量等值匹配就略去不表，因为它和switch-case功能完全相同。即使如此，模式匹配在这个特性上也更出色。比如Java的switch-case类型只支持整数类型或可隐式转换成整数类型得变量的匹配。而模式匹配则支持所有类型的变量的匹配。

元组匹配

        模式匹配不止支持单一变量，还支持多变量，请看如下Scala代码：

def processUser(userID:int, type:int,state:int){

       (type,state) match {

              case(1, 10) => processA(userID)

              case(2, _) => processB(userID)

              case_ => process(userID)

    }

}

        在上述代码中，如果类型为1并且状态为10的用户，接受processA处理；而类型为2的用户接受processB处理，这时不考虑状态如何；其他所有情况的用户接受process函数处理，下划线表示匹配相应变量的任何值。

        这个功能用if-else实现也很容易，但是可读性如何则一目了然。

从上面的例子中还可以看出，模式匹配后面是不能再有代码的，因为根本走不到，=>符号的含义为返回，即return。这样也间接体现了函数式语言强调函数的单一功能和小型化原则。

        最后，模式匹配中因为每个匹配都意味着函数返回，因此就不需要switch-case中每个case匹配都要break一下了。

集合匹配和抽取

        模式匹配还可以支持集合的匹配，并在匹配成功时顺便获取集合中的匹配元素。下面的Scala代码将参数中两个List的第一个元素加和并返回，如果有一个为空则返回null：

def addFirstElement(listA: List[Integer],listB: List[Integer]): Integer = {

       (listA,listB) match {

              case(List(), _) => null

              case(_, List()) => null

              case(firstA::tailA, firstB::tailB) => firstA+firstB

    }

}

        上面的匹配中，List()代表空集合；firstA::tailA这个表达式的含义是匹配List有至少一个元素的情况，同时顺便把List的第一个元素赋值到firstA中，而tailA是一个列表，是原列表中除了第一个元素之外剩下的列表。

        不同的函数式语言对模式匹配中的集合匹配支持程度都不同，感兴趣的话可以参见参考资料中各个语言的技术书籍。

对象匹配和抽取

        模式匹配支持的另一个重要匹配是自定义类对象的匹配，这也体现了函数式编程和面向对象编程结合下的多范型编程。

        在元组匹配的例子中，processUser函数有三个参数，在面向对象编程中，这三个参数实际上可以封装到User类中，这时就需要对User类进行匹配，代码变化如下：

def processUser(user: User){

       usermatch {

              caseUser(userID, 1, 10) => processA(userID)

              caseUser(userID, 2, _) => processB(userID)

              caseUser(userID, _, _) => process(userID)

    }

}

        这里有个前提，就是User类必须具备多参数构造方法，用来初始化内部成员。

        匹配过程用到User类的多参数构造方法，每个参数代表User的一个成员变量。在第一个case中，匹配的是user对象type字段为1，state字段为10的情况，同时抽取出user对象的id字段到userID变量中，使得我们可以在=>后面的匹配处理中使用这个字段。

守卫条件

        你可能已经发现，目前讲的模式匹配都是等值匹配，那类似于大于或小于这种基于布尔值的匹配之中该如何写呢？

        模式匹配中有个守卫条件的概念，就是专门解决这个问题，只有布尔条件满足才可以进行相应处理。Haskell语言支持守卫条件，示例如下：

testBodySize weight height

       |bmi <= 18.5 = “you are underweight”

       |bmi <= 25.0 = “you are normal”

       |bmi <= 30.0 = “you are fat”

       |otherwise  = “you are joking?”

       wherebmi = (weight/height)^2

        上述函数testBodySize用来测试一个人的身材，参数是人的宽度和身高。

        |符合代表每一个匹配项，而where是关键字，用来在模式匹配中声明共用的变量，这里声明变量bmi用来保存此人的宽度和身高的比值平方。Haskell规定一旦在函数中出现模式匹配的相关代码，就不能出现任何局部变量的声明和过程式编程中的各种代码，想声明变量的话可以通过where关键字解决。

        每一个匹配项就是一个布尔表达式，从前向后依次进行条件判断，如果发现守卫条件满足，则返回相应的字符串。关键字otherwise是兜底条件，类似于switch-case语句中的default关键字。

部分函数

        部分函数（partial function）：指定了参数的取值或者取值范围的函数，如果传入了不在范围的参数，函数将执行预定的例外处理。也就是说，函数式编程语言中的部分函数概念和数学里的偏函数概念是一样滴。

        你能会想，要实现部分函数也太简单了，在函数最开始判断一下参数不就得了？超出范围就抛个参数不合法的异常，典型的防御性编程嘛。这样做当然没有问题，但是函数式编程有自己的方式，就是利用上文介绍的模式匹配。

        Scala具有一个PartialFunction类型，自己创建一个类继承它，就可以实现部分函数了。对于大部分函数式编程语言，通常使用上文介绍的模式匹配实现部分函数，比如Scala和Haskell。具体实现就是语言细节了，大家可以自行查看，不再赘述。

        最后需要注意的是，有的编程语言把部分函数和偏应用函数这两个概念弄的比较含混。比如在Python中，Partial Function指的是偏应用函数，而没有部分函数的概念。因此需要大家在学习具体的函数式编程语言时注意区分相关概念。

结论

        本文介绍了函数式编程的必备概念，从简单的函数、闭包概念，到复杂的Functor和Monad概念。深入研究这些概念之后你会发现，你考虑问题的方式和编程的方式都变化了，也许这就是函数式编程对于熟练的Java或C++程序员难以学习的原因。并不是掌握了这些概念就能学会函数式编程，而是要从思维方式也转变为函数式的，否则即使一种多范型语言提供了函数式编程支持，你也不会去用。参考资料[8]提供了这样一种思维转变。

        实际上，很多现有的语言都或多或少的提供了函数式编程特性支持，参考资料[1-7]分别提供Haskell、Scala、Python、Javascript和Java的函数式编程学习指南。

        本文的编程编程范型和基本语言结构的论述参考了[15]，参考资料[13][14]是Philip Wadler关于Monad和诸多函数式特性的原始论文，有兴趣的话可以深入探究一下大神的世界。

        我想大家已经跃跃欲试函数式编程了，大胆的去用吧，下一篇文章将涉及函数式编程的应用，到时我们一同探讨。

参考资料

[1] Learn You A Haskell For Great Good!.Miran Lipovacˇ a. 2011.

[2] Scala in Depth. JOSHUA D. SUERETH.2012.

[3] Functional Programming in Scala. PAULCHIUSANO. 2014.8.

[4] Programming in Scala, Second Edition. MartinOdersky. 2010.12.

[5] Fluent Python. Luciano Gama de SousaRamalho. 2015.8.

[6] Functional JavaScript. Michael Fogus.2013.5.

[7] Java 8 in Action: Lambdas, streams, andfunctional-style programming. Raoul-Gabriel Urma. 2015.

[8] Becoming Functional. Joshua Backfield.2014.6.

[9] Functors, Applicatives, And Monads InPictures.http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html.2013.

[10] Monads for the Curious Programmer,Part 1.http://bartoszmilewski.com/2011/01/09/monads-for-the-curious-programmer-part-1/.2011.

[11] Monads for the Curious Programmer:Part 2.http://bartoszmilewski.com/2011/03/14/monads-for-the-curious-programmer-part-2/.2011.

[12] Monads for the Curious Programmer:Part 3.http://bartoszmilewski.com/2011/03/17/monads-for-the-curious-programmer-part-3/.2011.

[13] Monads for functional programming. PhilipWadler. 1995.

[14] The Essence of Functional Programming.Philip Wadler. 1992.

[15] 程序设计语言原理. 麦中凡, 吕卫峰. 2011

[16] Closure. https://en.wikipedia.org/wiki/Closure_(computer_programming).

[17] Monoid. https://en.wikipedia.org/wiki/Monoid.

[18] Currying. https://en.wikipedia.org/wiki/Currying.

附录A

        下面我们尝试证明这个引理，代码为类似Python的伪代码。

        思路很简单，我们利用map、join和Wrapper构造函数构造出map2函数。高阶函数map2的函数实现如下：

def map2(((X, Y) => Z) f2): (Wrapper,Wrapper) => Wrapper {

        def F2(Wrapper wx, Wrapper wy): Wrapper{

             def middle(X x): Wrapper{

                     return map(f2(x))(wy);

              }

              return flatMap(middle)(wx);

         }

         returen F2;

}

        我们需要构造的函数map2是高阶函数，参数是一个带有两个参数的函数f2，返回值也是一个函数，返回函数也带有两个参数，都是原类型的Wrapper包装类型参数。

        我们在函数内部定义一个函数F2，这个F2函数就是我们需要返回的函数，最后的return语句只需将F2返回即可。我们只需集中精力实现F2函数。

        我们在F2内部定义了一个辅助函数middle，这个函数以X类型的参数返回Wrapper类型值，因为我们现有的map函数需要的是单参数函数，因此我们必须先固定一个函数参数。函数f2(x)返回的就是一个单参数函数（还记得函数的偏应用么？），函数f2(x)返回值类型是Y => Z，这个把这个参数传递到map函数，得到的结果将是函数Wrapper => Wrapper，然后我们再把F2的参数wy传递进去，就得到了Wrapper类型的结果。这些过程仅仅用一条语句就搞定了：return map(f2(x))(wy)

        flatMap函数是一个重要的辅助函数，它的函数类型如下：

(X => Wrapper) =>(Wrapper => Wrapper)

        flatMap也是一个高阶函数，它以(X =>Wrapper)类型函数为参数，以(Wrapper => Wrapper)类型的函数为返回值。

        假设我们已经有了flatMap，那么我们正好可以把刚才定义的middle函数传递进去，获得的结果是Wrapper => Wrapper类型的函数，我们的F2函数的两个参数只剩下了wx还没有用过，把wx传递进去，我们获得了Wrapper类型的值，然后将其返回，F2函数构造完毕，map2函数也就完成了。

        下面我们集中精力构造flatMap函数：

def flatMap((X => wrapper) fm):Wrapper => Wrapper {

       def Fm(Wrapper wx): Wrapper {

              varwwz = map(fm)(wx);

              returnjoin(wwx);

       }

       return Fm;

}

        还是老思路，我们直接在函数内部定义一个Fm函数，其类型为Wrapper => Wrapper，实现完成后，我们直接把这个函数返回即可。

        Fm函数的实现就两行代码，使用了map和join函数。

         函数应用map(fm)返回的函数类型是Wrapper => Wrapper>，之所以是Wrapper>而不是Wrapper，是因为fm是X =>Wrapper而不是X => Z。那么变量wwx的类型就是Wrapper>了。

        还记得join函数么？它终于派上用场了，它通过Wrapper>类型的变量获得Wrapper类型的变量，即完成降维。这样，将结果直接返回即可，Fm构造完成。

        至此，我们完成了map2函数的构造，全程仅仅使用了map函数和join函数，引理得证。

        需要指出的是Monad和Functor的区别仅仅在于join的有无上，而引理需要join函数，因此该引理只针对Monad成立，对于Functor是不成立的。

        最后，引理的证明实际上是综合应用了函数式编程中的高阶函数特性、闭包特性和函数偏应用特性，也是一个不错的学习案例。