李航老师《统计学习方法》第二版第二章答案
1、Minsky与Papert指出:感知机因为是线性模型,所以不能表达复杂的函数,比如异或(XOR)。验证感知机为什么不能表示异或。
解:
下面是异或的运算结果:
异或: 如果两个值相同则异或操作的结果是0,如果不相同则为1
由此我们可以看到,这也是一个二分类的问题,异或的运算如表所示
| XOR | a | b |
|---|---|---|
| a | 0 | 1 |
| b | 1 | 0 |
方法一:直观作图法
如果我们去a = 0, b = 1,将上表的结果画在二维平面,如下图。
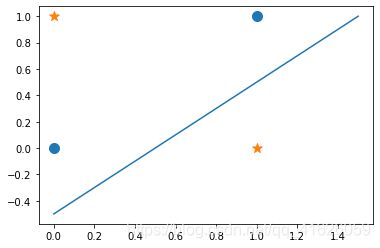
我们可以看到,对于蓝色的圆点和橙色的星星,无论我们怎么画直线,都不可能将两者分开。也就是我们不能画出一条直线,是蓝色的圆点位于直线的一侧,是两个橙色的星星位于直线的另外一侧,因而,感知机无法表示异或(XOR)。
方法二:直接计算法
设正例的点是:(0, 0)和(1, 1),负例的点是:(1,0)和(0,1)
我们假设这两类是可以线性分开的,设 f = w 1 x 1 + w 2 x 2 + b f = w_{1}x_{1}+w_{2}x_{2}+b f=w1x1+w2x2+b为对应的线性模型
由上面的假设可以知道点(0,0)和点(1,1)使 f > 0 f>0 f>0成立;
而点(1,0)和(0,1)使 f < 0 f<0 f<0成立。
将点(0,0)和点(1,1)代入我们得到:
{ 0 + 0 + b > 0 w 1 + w 2 + b > 0 (1) \left\{ \begin{aligned} 0+0+b>0 \\ w_{1}+w_{2}+b>0 \\ \end{aligned} \right.\tag{1} { 0+0+b>0w1+w2+b>0(1)
将点(1,0)和(0,1)代入我们得到
{ w 1 + 0 + b < 0 0 + w 2 + b < 0 (2) \left\{ \begin{aligned} w_{1}+0+b<0 \\ 0+w_{2}+b<0 \\ \end{aligned} \right.\tag{2} { w1+0+b<00+w2+b<0(2)
将等式(1)中的两式相加,我们得到
w 1 + w 2 + 2 b > 0 (3) w_{1}+w_{2}+2b>0\tag{3} w1+w2+2b>0(3)
将等式(2)中的两式相加我们得到
w 1 + w 2 + 2 b < 0 (4) w_{1}+w_{2}+2b<0\tag{4} w1+w2+2b<0(4)
联合公式(3)和(4),得出矛盾,因此不能线性可分。
方法3:使用这一章课后题的第三题来做
我们知道连接点(0,0)和(1,1)的直线段和连接点(1,0)和(0,1)的直线段在(0.5,0.5)处相交,也就是两个点集的凸壳是相交的,因而不可能线性可分。
2、模仿例题2.1,构建从训练数据集求解感知机模型的例子。
解:
这里不再构造,而是使用python将两种算法针对书上的例题2.1,将其实现出来。
import numpy as np
import matplotlib.pyplot as plt
epoch = 10
def Original_Percetron(x, y, lr = 0.1):
'''
Parameters
----------
x : numpy array
训练数据集.
y : numpy array
训练集标签.
lr : float
梯度下降算法学习率
Returns
-------
返回参数,并画出分割超平面.
'''
#先获取训练集的维度
s = np.shape(x)
#初始化感知机模型参数
w = np.zeros(shape = (1, s[1]))
b = np.array(0.0)
#下面开始更新模型
for e in range(epoch):
for i in range(s[0]):
x_i = x[i: i + 1]
if y[i] * (np.matmul(w, x_i.T)[0, 0] + b) <= 0:
w = w + lr * y[i] * x_i
b = b + lr * y[i]
print('训练%d个epoch后参数是:'%epoch, 'w 是:', w, 'b 是:', b)
#下面开始画图
num_positive = sum(np.array(y == 1, dtype = np.int64))
plt.scatter(x[:num_positive, 0], x[:num_positive, 1], marker = "*", s = 100)
plt.scatter(x[num_positive:, 0], x[num_positive:, 1], marker="o", s = 100)
x11 = min(x[:,0]) - 1
x12= max(x[:,0]) + 1
x21 = - (w[0, 0] / w[0, 1]) * x11 - b / w[0, 0]
x22 = - (w[0, 0] / w[0, 1]) * x12 - b / w[0, 0]
plt.plot([x11, x12], [x21, x22])
def Dual_Perceptron(x, y, lr = 0.1):
'''
Parameters
----------
x : numpy array
训练数据集.
y : numpy array
训练集标签.
lr : float
梯度下降算法学习率
Returns
-------
返回参数,并画出分割超平面.
'''
s = np.shape(x)
#下面先计算Gram矩阵
G = np.matmul(x, x.T)
alpha = np.zeros(shape = (s[0]))
for e in range(epoch):
for i in range(s[0]):
if y[i] * (sum(lr * alpha * y * G[:, i] + lr * alpha * y)) <= 0:
alpha[i] += 1
#下面开始画图
num_positive = sum(np.array(y == 1, dtype = np.int64))
plt.scatter(x[:num_positive, 0], x[:num_positive, 1], marker = "*", s = 100)
plt.scatter(x[num_positive:, 0], x[num_positive:, 1], marker="o", s = 100)
x11 = min(x[:,0]) - 1
x12= max(x[:,0]) + 1
w = np.zeros(shape = (s[1]))
b = 0.0
for i in range(s[0]):
w = w + alpha[i] * y[i] * x[i] * lr
b = b + alpha[i] * lr * y[i]
x21 = - (w[0] / w[1]) * x11 - b / w[0]
x22 = - (w[0] / w[1]) * x12 - b / w[0]
plt.plot([x11, x12], [x21, x22])
if __name__ == '__main__':
x = np.array([[3,3],
[4,3],
[1,1]])
y = np.array([1,1,-1])
Original_Percetron(x, y, lr = 0.1)
Dual_Perceptron(x, y, lr = 0.1)
3、证明一下定理:样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集构成的凸壳互不相交。
证明:
充分性:由凸壳不相交推导线性可分
因为正实例和负实例分别构成的凸壳是不相交的,因而,一定有一个超平面将两个凸壳线性分开,再根据凸壳的定义可以看到,正实例点一定在正实例点集构成的凸壳里面,负实例点一定在负实例点集构成的凸壳内,因而既然可以将两个凸壳分开,那么也可以将两类点集分开。
其实这个充分性的证明还是比较显然的,下面再提供一种数学方面的思路。
设 d = i n f x , y d ( x , y ) (1) d = \underset{x,y}{inf}\quad d(x,y) \tag{1} d=x,yinfd(x,y)(1)
其中 x , y x,y x,y 分别是两个凸壳中的点, d ( x , y ) d(x,y) d(x,y) 表示 x , y x,y x,y 两点之间的距离。
因为凸壳是闭集,所以一定可以在两个凸壳内找到两点 x , y x,y x,y,使得 x , y x,y x,y 之间的距离就是这两个凸壳之间的距离,然后,我们做 x , y x,y x,y 两点的垂直平分线,该垂直平分线就是我们要找的分割平面。
必要性:已知线性可分,证明两个凸壳不相交。
设集合 A , B A,B A,B分别是正实例和负实例对应的点集,标记 y A = 1 , y B = − 1 y_{A} = 1,y_{B} = -1 yA=1,yB=−1,因为 A , B A,B A,B线性可分,所有设 f = w x + b (2) f = wx+b\tag{2} f=wx+b(2)为分割超平面。
所以对于任何一点 x i A ∈ A , x j B ∈ B x_{i}^{A}\in A,x_{j}^{B}\in B xiA∈A,xjB∈B,我们都有
w ∗ x i A + b > 0 (3) w*x_{i}^{A}+b>0\tag{3} w∗xiA+b>0(3)
w ∗ x j B + b < 0 (4) w*x_{j}^{B}+b<0\tag{4} w∗xjB+b<0(4)
如果两个凸壳相交,那么一定有集合 A A A中的点在 c o n v ( B ) conv(B) conv(B)内或者有集合 B B B内的点在凸壳 c o n v ( A ) conv(A) conv(A)内。或者有 c o n v ( A ) conv(A) conv(A)的内点在 c o n v ( B ) conv(B) conv(B)内。
不妨假设前者成立,也即是有集合 A A A中的点 x i A x_{i}^{A} xiA 在 c o n v ( B ) conv(B) conv(B)内。如果只是 c o n v ( A ) conv(A) conv(A)的 内点 a a a 在 c o n v ( B ) conv(B) conv(B)内,因为 a a a 是集合 A A A中点的线性组合,证明也是类似的。所以我们下面只证明集合 A A A中的点 x i A x_{i}^{A} xiA 在 c o n v ( B ) conv(B) conv(B)内。
也就是 x i A ∈ c o n v ( B ) x_{i}^{A}\in conv(B) xiA∈conv(B),所以 A A A内的点 x i A x_{i}^{A} xiA可以被 B B B内的点进行凸组合表示,不妨设为:
x i A = ∑ j = 1 N λ j x j B (5) x_{i}^{A} = \sum_{j = 1}^{N}\lambda _{j}x_{j}^{B}\tag{5} xiA=j=1∑NλjxjB(5)
但是根据公式(3)我们得
w ∗ x i A + b > 0 w*x_{i}^{A}+b>0 w∗xiA+b>0
但是
w ∗ x i A + b = w ∗ ∑ j = 1 N λ j x j B + b = ∑ j = 1 N λ j w x j B + b = ∑ j = 1 N λ j w x j B + ∑ j = 1 N λ j b = ∑ j = 1 N λ j ( w ∗ x j B + b ) < 0 (6) w*x_{i}^{A}+b = w*\sum_{j = 1}^{N}\lambda _{j}x_{j}^{B} + b \\=\sum_{j = 1}^{N}\lambda _{j}wx_{j}^{B}+b \\=\sum_{j = 1}^{N}\lambda _{j}wx_{j}^{B}+\sum_{j = 1}^{N}\lambda _{j}b \\=\sum_{j = 1}^{N}\lambda _{j}(w*x_{j}^{B}+b)<0\tag{6} w∗xiA+b=w∗j=1∑NλjxjB+b=j=1∑NλjwxjB+b=j=1∑NλjwxjB+j=1∑Nλjb=j=1∑Nλj(w∗xjB+b)<0(6)
因而矛盾,所以 c o n v ( A ) , c o n v ( B ) conv(A),conv(B) conv(A),conv(B)一定不相交的。
综上,得证!!!