一文搞定（三） —— 高斯过程回归 Gaussian Process Regression

2021.03.07 更新： 优化了 section 1 的内容，删去文章原先结构中的 2、3 两个 section（这两部分涉及高斯过程的权重空间视角，因并不实用且易产生混淆而得到删除，但其完整内容仍然可以在作者的个人博客中查看：链接 ）
2021.03.27 更新： 丰富了 section 2 的内容，添加了更多图像化的、从而易于理解的表述。

---

【参考资料】
1.B站：机器学习-白板推导系列(二十)-高斯过程GP(Gaussian Process)
2.CSDN：一文搞定（二）—— 贝叶斯线性回归
3.知乎：Gaussian process regression的导出——权重空间视角下的贝叶斯的方法
4.知乎：高斯过程 Gaussian Processes 原理、可视化及代码实现

【文章结构】
1 Introduction: 从高斯分布到高斯过程
2 高斯过程回归 Gaussian Process Regression
3 代码示例 （包含对于一个简单 GPR 示例的 python 和 matlab 两种语言的代码）

1 Introduction: 从高斯分布到高斯过程

1.1 多元高斯分布

$$p(\mathbf{x})=\prod _{i=1}^{n}p(x_i)=\frac{1}{(2\pi {)}^{\frac{n}{2}}{\sigma }_1...{\sigma }_n}\exp (-\frac{1}{2}[\frac{(x_1-{\mu }_1{)}^2}{{\sigma }_1^2}...\frac{(x_n-{\mu }_n{)}^2}{{\sigma }_2^2}])\text{\hspace{1em}(1)}$$
进一步的，令

1. $\mathbf{x}-\mathbf{\mu }=[x_1-{\mu }_1,...,x_n-{\mu }_n{]}^T$
2. $\mathbf{\Sigma }=\left[\begin{array}{cccc}{\sigma }_1^2& 0& ...& 0\\ 0& {\sigma }_2^2& ...& 0\\ ...& ...& ...& ....\\ 0& ...& 0& {\sigma }_n^2\end{array}\right]$

从而可得多元高斯分布的向量化表示：

$$p(\mathbf{x})=(2\pi {)}^{-\frac{n}{2}}|\mathbf{\Sigma }{|}^{-\frac{1}{2}}\exp (-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T|\mathbf{\Sigma }{|}^{-1}(\mathbf{x}-\mathbf{\mu }))\text{\hspace{1em}(2)}$$

（留意上式中的 $(\mathbf{x}-\mathbf{\mu }{)}^T|\mathbf{\Sigma }{|}^{-1}(\mathbf{x}-\mathbf{\mu })$，它与下文将要介绍的 kernel function 有着类似的形式）

1.2 高斯过程 Gaussain Process

高斯过程是定义在连续域上的无限多个高维随机变量所组成的随机过程，可以看做是一个无限维的高斯分布。在作者的理解中，通过高斯过程，我们能够将离散的点分布转化为函数的分布。

借用参考资料 4 中的插图，高斯过程在下图中的体现就是将红色的离散点变成蓝色的函数曲线（该曲线不仅能够储存原离散数据集的部分特征，还能用于预测）：

GP 的数学定义

对于随机变量 $\{{\zeta }_t{\}}_{t\in T}$ （$T$ 可以是连续的时间或空间），如果对于任意 $n\in {\mathbb{N}}^{+},t_1,...,t_n\to {\zeta }_1,...,{\zeta }_n$, 都有 $\mathbf{\zeta }=({\zeta }_1,...,{\zeta }_n{)}^T\sim N(\mathbf{\mu },\mathbf{\Sigma })$, 那么 $\{{\zeta }_t{\}}_{t\in T}$ 就是一个高斯过程，记做
$${\zeta }_t\sim GP(m(t),\kappa (s,t))\text{\hspace{1em}(3)}$$

1. $m(t)=E[{\zeta }_t]$, mean function
2. $\kappa (t,s)=E[({\zeta }_s-m(s))({\zeta }_t-m(t){)}^T]$, covariance function

2 高斯过程回归 Gaussian Process Regression

假设样本集 $\{f(x)\}$ 满足：
$$\{f(x){\}}_{x\in {\mathbb{R}}^p}\sim GP(m(x),\kappa (x,x^{\prime }))$$

1. $m(x)=E[f(x)]$
2. $\kappa (x,x^{\prime })=E[(f(x)-m(x))(f(x^{\prime })-m(x^{\prime }){)}^T]$

2.1 回归 Regression

给定数据集,
$$D=\{(x_i,y_i){\}}_{i=1}^N,y=f(x)+\epsilon$$

where, $\epsilon \sim N(0,\sigma )$

定义 $X=[(x_1,...,x_N{)}^T{]}_{N\times p},Y=[(y_1,...,y_N{)}^T{]}_{N\times 1}$，再结合先前的假设可得：
$$\begin{gathered} f(X)\sim N(\mu (X),\kappa (X,X)) \\ Y=f(X)+\epsilon \sim N(\mu (X),\kappa (X,X)+{\sigma }^{2}I) \end{gathered}$$

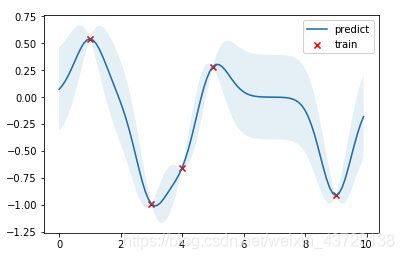
至此我们完成了 GPR 的回归部分。以下图为例（同 section 1.2 中的图）：回归 在这张图里的体现就是提取了数据点（红叉叉）所包含的已知数据集的特征信息，并将其转换为了一个高斯模型。（注：上文中的特征信息主要包含两个方面，一个是自变量信息，例如下图中的 x 轴数值，当然可以是多维的；另一个是因变量信息，例如下图中的 y 轴数值）

2.2 预测 Prediction

给定需要预测的数据 $X^{\ast }=(x_1^{\ast },...,x_M^{\ast }{)}^T$，求 $Y^{\ast }$
$$\left(\begin{array}{c}Y\\ f(X^{\ast })\end{array}\right)\sim N\left(\begin{array}{c}\left(\begin{array}{c}\mu (X)\\ \mu (X^{\ast })\end{array}\right),\left(\begin{array}{cc}\kappa (X,X)+{\sigma }^{2}I& \kappa (X,X^{\ast })\\ \kappa (X^{\ast },X)& \kappa (X^{\ast },X^{\ast })\end{array}\right)\end{array}\right)$$

已知公式，对于 $X\sim N(\mu ,\Sigma )$
$$\begin{gathered} \text{If}X=\left(\begin{array}{c}{X}_a\\ X_b\end{array}\right),\mu =\left(\begin{array}{c}{\mu }_a\\ {\mu }_b\end{array}\right),\Sigma =\left(\begin{array}{cc}{\Sigma }_{aa}& {\Sigma }_{ab}\\ {\Sigma }_{ba}& {\Sigma }_{bb}\end{array}\right) \\ \text{then }{X}_b|X_a\sim N({\mu }_{b|a},{\Sigma }_{b|a}) \end{gathered}$$

where,

1. ${\mu }_{b|a}={\Sigma }_{ba}{\Sigma }_{aa}^{-1}(X_a-{\mu }_a)+{\mu }_b$
2. ${\Sigma }_{b|a}={\Sigma }_{bb}-{\Sigma }_{ba}{\Sigma }_{aa}^{-1}{\Sigma }_{ab}$

根据该公式可得
$$P(f(X^{\ast })|Y,X,X^{\ast })=P(f(X^{\ast })|Y)\sim N({\mu }^{\ast },{\Sigma }^{\ast })$$

where,

1. ${\mu }^{\ast }=\kappa (X^{\ast },X)(\kappa (X,X)+{\sigma }^{2}I{)}^{-1}(Y-\mu (X))+\mu (X^{\ast })$
2. ${\Sigma }^{\ast }=\kappa (X^{\ast },X^{\ast })-\kappa (X^{\ast },X)(\kappa (X,X)+{\sigma }^{2}I{)}^{-1}\kappa (X,X^{\ast })$

最终可得，
$$P(y^{\ast }|Y,X,X^{\ast })\sim N({\mu }^{\ast },{\Sigma }^{\ast }+{\sigma }^{2}I)$$

至此我们完成了 GPR 的预测部分。依旧以同样的一幅图为例：预测 在这张图里的体现就是根据 回归 得到的信息，预测其他点位的函数值及其标准差（蓝色线条以及浅蓝色区域）。

3 代码示例

简单高斯过程回归实现
(斜体部分内容来自参考资料 4)

考虑代码实现一个高斯过程回归，API 接口风格采用 sciki-learn fit-predict 风格。由于高斯过程回归是一种非参数化 (non-parametric) 的模型，每次的 inference 都需要利用所有的训练数据进行计算得到结果，因此并没有一个显式的训练模型参数的过程，所以 fit 方法只需要将训练数据保存下来，实际的 inference 在 predict 方法中进行。

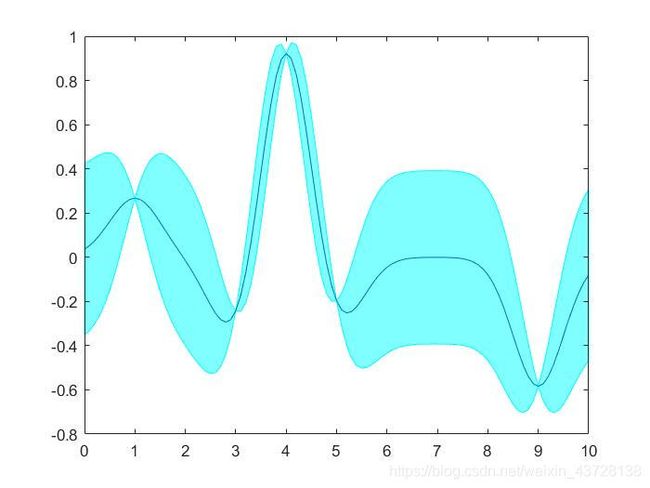
结果如下图，红点是训练数据，蓝线是预测值，浅蓝色区域是 95% 置信区间。真实的函数是一个 cosine 函数，可以看到在训练数据点较为密集的地方，模型预测的不确定性较低，而在训练数据点比较稀疏的区域，模型预测不确定性较高。

python 实现

详见 参考资料 4

matlab 实现

定义类

classdef GPR
    properties
        is_fit = 0;
        train_X = nan;
        train_y = nan;
        params = struct('l', 0.5, 'sigma_f', 0.2);
    end
    
    methods
        function obj = GPR()
        end
        
        function obj = fit(obj, X, y)
            obj.train_X = X;
            obj.train_y = y;
            obj.is_fit = 1;
        end
        
        function [mu, cov] = predict(obj, X)
            if obj.is_fit == 0
                disp('model not fit yet')
            end
            
            Kff = obj.kernel(obj.train_X, obj.train_X);
            Kyy = obj.kernel(X, X);
            Kfy = obj.kernel(obj.train_X, X);
            Kff_inv = inv(Kff + 1e-8 * eye(length(obj.train_X)));
            
            mu = Kfy' * Kff_inv * obj.train_y;
            cov = Kyy - Kfy' * Kff_inv * Kfy;
        end
        
        function result = kernel(obj, x1, x2)
            distance = x1.^2 + (x2.^2)' - 2 * x1 * x2';
            sigma_f = obj.params.('sigma_f');
            l = obj.params.('l');
            result = sigma_f^2 * exp(-distance/(2*l^2));
        end    
    end
end

训练 + 预测

train_X = [3, 1, 4, 5, 9]';
train_y = cos(train_X);

test_X = 0:0.1:10;
test_X = test_X';

gpr = GPR();
gpr = gpr.fit(train_X, train_y);
[mu, cov] = gpr.predict(test_X);

uncertainty = 1.96 * sqrt(diag(cov));
figure;
xfill = [test_X', fliplr(test_X')];
yfill = [(mu - uncertainty)', fliplr((mu + uncertainty)')];
fill(xfill, yfill, 'c', 'FaceAlpha', 0.5, 'EdgeAlpha', 1, 'EdgeColor', 'c');
hold on;
plot(test_X, mu);

结果示意图