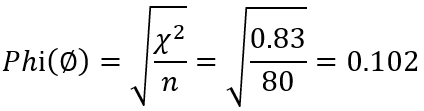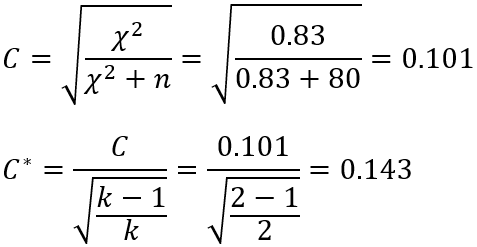二分类变量相关性分析spss_SPSS分析技术：两个定类变量的相关系数(1)

基础准备

前面草堂君给大家详细介绍了各种相关系数种类，不同的相关系数用来表示不同类型变量之间的相关关系强弱，大家可以点击下方文章链接回顾：

• 统计理论深度阅读：相关系数家谱(第一部)

• 统计理论深度阅读：相关系数家谱(第二部)

接下来草堂君将给大家详细介绍不同相关系数的实际应用场景以及如何使用统计软件进行计算。知其然知其所以然，才能融会贯通和触类旁通。

相关分析的作用

开始正式文章前，草堂君先帮大家回顾一下相关分析的作用。相关分析能够得到两个结果，一个是显著性结果(p值)，表示两个(组)变量是否是显著性相关；另一个相关系数，它用来表示两个变量的相关强度有多强，一般相关系数都在-1~1之间，越接近1和-1代表相关强度越强(正向和负向)，越接近0，代表强度越弱。

相关系数越接近0，显著性(p值)约大，一般大于0.05(当然常用的显著性水平还有0.1、0.01和0.001)就认为两个变量没有显著性相关了；相关系数越接近-1或1，显著性(p值)越小，一般小于0.05就认为两个变量显著性相关了。

两个分类变量的相关系数

根据草堂君前面的介绍，适用于两个分类变量的相关系数有Phi系数、列联系数C(矫正列联系数C*)、Tshuprow‘s T系数、Cramer’s V系数、Theil‘s U系数和lambda系数。其中，Phi系数适用于2*2列联表；列联系数C和Tshuprow’s T适用于n*n列联表；Cramer’s V、lambda和Theil‘s U适用于n*m列联表。

如上表所示，因为红色字体的四个相关系数都是基于卡方值设计的，所以今天草堂君先介绍前四种相关系数以及它们的案例应用和分析过程。

Phi系数

首先回顾Phi系数的计算公式，如下所示。从公式可知，Phi系数对卡方值进行了样本量修正，表示为平均到每个样本上的平均比率差异有多少，平均差异越大，Phi系数越大，表示两个定类型变量不是独立无关的，也就是两个定类型变量越相关。需要注意，如果两个定类型变量的水平数都大于2(例如，有三个药品种类，水平数为3)，那么Phi系数是有可能大于1的，这和我们熟悉的相关系数介于-1~1之间的共识相左，因此，Phi系数常用再2*2列联表情况下。

案例分析1

现在有两种质量方案A和B，需要研究它们的治疗效果。随机选取了80个某种疾病的患者进行实验，实验结果如下表所示：

分析过程

因为是2*2的列联表，所以Phi相关系数是适用于表示本案例两个分类型变量治疗效果和治疗方案之间相关强度的。计算结果如下：

列联系数和矫正列联系数

因为Phi系数用于定类型变量水平数大于2时，Phi系数可能会大于1，所以设计出列联系列，联系数是Phi系数的扩展运用。从公式可知，列联系数相比于Phi系数，分母多加了一个卡方值，这样就能够避免当列联表大于2*2时，系数大于1的情况；但是，与此同时，在列联表比较小或列联表不是对称时，列联系数对两个分类变量的相关性描述会造成低估，因此，又设计出矫正列联系数，适用于小列联表和非对称列联表。因此，列联系数适用于3*3，4*4和5*5的列联表，而矫正列联系数适用于非对称性和3*3以下的列联表，从这个角度来说，矫正列联系数和Phi系数是相当的。

首先用案例分析1中的数据计算列联系数和矫正列联系数，对比它们与Phi系数的大小差异。计算结果如下：

通过上面的计算结果可知，Phi系数介于列联系数和矫正列联系数之间，列联系数用在小尺寸列联表会低估两个变量之间的相关强度。

案例分析2

将案例1的实验稍加改动。现在有三种质量方案A、B和C，需要研究它们的治疗效果。随机选取了273个某种疾病的患者进行实验，实验结果如下表所示：

计算过程

本案例是3*3的列联表，因此适用列联系数表示治疗效果和治疗方案之间的相关性。计算结果如下所示：

Tshuprow‘s T系数

对于尺寸大于5*5的列联表，则采用Tshuprow‘s T系数来描述两个定类型变量的相关性，因为它考虑了行和列的自由度，需要注意，当行和列都等于2时，Tshuprow’s T系数等于Phi系数。如下面的等式所示。

将Tshuprow‘s T的计算公式带入案例1和案例2进行计算，计算结果如下。由计算结果可知，对于Tshuprow’s T系数来说，它的值比上面的Phi，列联系数和矫正列联系数都小，由此可见，Tshuprow‘s T系数适用于大尺寸的列联表(5*5以上)。

Cramer’s V系数

前面几个相关系数都是适用于对称性列联表的情况，Cramer’s V适用于行变量和列变量的水平数不同的情况。从公式可知，Cramer’s V系数在分母位置矫正了更小的自由度。

案例分析3

将案例1的实验稍加改动。现在有四种质量方案A、B、C和D，需要研究它们的治疗效果。随机选取了160个某种疾病的患者进行实验，实验结果如下表所示：

计算过程

本案例是2*4列联表，为非对称列联表，因此适用Cramer’s V系数表示治疗效果和治疗方案之间的相关性。计算过程如下所示：

软件操作

适用SPSS软件可以计算以上介绍的Phi、列联系数、Cramer’s V系数。点击【分析】-【描述统计】-【交叉表】，跳出如下对话框，点击统计按钮，可以看到在名义(定类数据)框内，有列联系数、Phi和Cramer‘s V系数选项。 

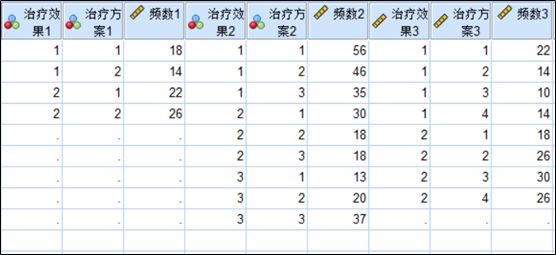
将上面三个案例数据输入到spss中，如下图所示。在进行分析之前，需要进行个案加权操作(操作过程可以回顾文章：SPSS分析技术：加权个案；让频数记录数据也能用SPSS做列联表分析)，然后再进行上方图片操作，即可输出结果。

(可前往qq群：577312904和134373751下载案例数据)

结果解释

从分析结果可知，适用spss计算的结果于上方公式计算结果相同。

总结一下

今天介绍的五种相关系数：Phi、列联系数、矫正列联系数、Tshuprow‘s T、Cramer’sV都是基于卡方值矫正的相关系数，差异在于矫正的角度和考虑不同(分母不同)。它们都用于表示两个定类型数据之间的相关性强弱，区别在于，对于不同尺寸情况的列联表，表示准确性上会有一些差异。需要注意，对于不同尺寸的列联表，它们都能计算出结果，大家可以根据实际情况考虑和选择。

平台的文章都是一文一例，所有例题的数据文件及SPSS软件都已上传到QQ群(群号：577312904)，需要对照练习数据分析技术的朋友可以前往下载。

温馨提示：

• 数据分析私人定制，一对一辅导，添加草堂君微信(possitive2)咨询！

• 生活统计学QQ群：577312904或134373751，用于分享文章提到的各种案例资料、软件、数据文件等。支持各种资料的直接下载和百度云盘下载。

• 生活统计学微信交流群，用于各自行业的数据研究项目及其成果交流分享；由于人数大于100人，请添加微信possitive2，拉您入群。

• 数据分析咨询，请点击首页下方“互动咨询”板块，获取咨询流程！