线代与计算机图形(一)
线代与计算机图形(一)
现代很有趣我要转专业了米娜桑
为什么是(一)呢,因为后面我还没学 ,额,当然是因为不知道你们还想不想看这种类型的,这篇先讲讲大家都喜欢的 数学。
本人大一学生,最近开始学习线代,老师告诉我们矩阵最开始是为了解决方程组问题产生的,但它神奇的成为计算机处理图形的十分有效的工具。对于矩阵的乘法有不同的理解方式,在这里我介绍和计算机图形相关的理解方法。
一、矩阵乘法的理解
左乘一个矩阵的实质是把右侧的向量映射到左乘的矩阵代表的坐标系中,本质上是一种坐标变换。
看一个例子,一段python代码。
import numpy as np
a=np.array([[1,2],[3,4]])
b=np.array([[2,0],[0,2]])
print(np.matmul(b,a))//矩阵乘法 矩阵b*矩阵a
输出结果是
[[2 4]
[6 8]]
我们通常把列数为一的矩阵叫做向量,这也就决定了我们的坐标变换是右乘一个矩阵
其实右边的矩阵是列向量集,也就是需要变换的坐标的集合,所以我们可以看到本来坐标为(1,3)的向量通过坐标变换变成了(2,6),同样的(2,4)这个向量变成了(4,8)。变换的结果是我们意料之中的,因为我们左乘的矩阵是系数矩阵(单位矩阵乘上某个常数),所以坐标是成2倍的扩大。
具体一点来看,这种变换实质就是基底的变换,比如(1,3)点基底选用的是i和j,i就对应着左乘矩阵的第一列,j就对应着左乘矩阵的第二列,也就是说左乘矩阵的第一行第二行分别对应着两个新的基底。
左乘旋转矩阵更好帮我们理解,如下:
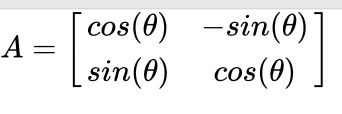
左乘着个矩阵相当于把向量以远点为圆心逆时针(因为人为规定这是正方向)旋转θ度。可以自己动手做做,多加思考一下就可以理解。
二、行列式的本质
那么看到这里有好兄弟就会问了,我们做这样的变换岂不是也会改变原来向量的大小,那么改变的这个大小具体是多少呢。不管你有没有这样的疑问,我都要说明:
其实左乘矩阵的行列式就是伸缩变换的扩大或者缩小的倍数,
那么你又会说了如果不是方阵呢?如果左乘矩阵不是方阵就意味着我们的坐标系变换是变换了维度的,也就意味着这种变换是不可逆的,
所以非方阵是没有可逆矩阵的!!!
三、关计算机啥事
说到这里那么这些关计算机什么事呢……
计算机的3维绘图中常常要用到矩阵变换,比如局部坐标系左乘平移矩阵变为世界坐标系,左乘旋转矩阵可以绕着某一轴旋转,还有正视投影矩阵、透视投影矩阵等等。以后有机会再写吧,毕竟日语专业的学生首要任务是学日语 。