神经网络隐藏层个数怎么确定_含有一个隐藏层的神经网络对平面数据分类python实现（吴恩达深度学习课程1第3周作业）...

含有一个隐藏层的神经网络对平面数据分类python实现（吴恩达深度学习课程1第3周作业）：

'''
题目：
建立只有一个隐藏层的神经网络，
对于给定的一个类似于花朵的图案数据，
里面有红色(y=0)和蓝色(y=1)，
构建一个模型来适应这些数据

planar_utils源代码在后文中
'''

import numpy as np
import matplotlib.pyplot as plt
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

#设置一个固定的随机种子，以保证接下来的步骤中我们的结果是一致的
#深度学习笔记：随机种子的作用:https://blog.csdn.net/qq_41375609/article/details/99327074?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.control
np.random.seed(1)

#导入数据
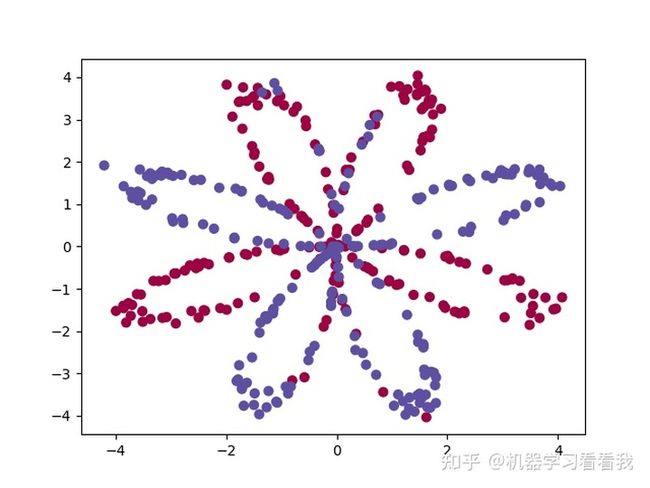
X,Y = load_planar_dataset()
plt.scatter(X[0,:],X[1,:],c=Y,s=40,cmap=plt.cm.Spectral)
plt.show()

#查看数据结构
print("X的维度为："+str(X.shape))
print("Y的维度为："+str(Y.shape))
print("数据集里面的数量为："+str(Y.shape[1]))
'''
输出：
X的维度为：(2, 400)
Y的维度为：(1, 400)
数据集里面的数量为：400
'''

#定义神经网络的大小
def layer_sizes(X,Y):
    n_x = X.shape[0] #输入神经元个数
    n_h = 4 #隐藏层，假设为4
    n_y = Y.shape[0] #输出层神经元个数
    return(n_x,n_h,n_y)

#初始化参数
def initialize_parameters(n_x,n_h,n_y):
    np.random.seed(2)
    W1 = np.random.randn(n_h,n_x)*0.01
    b1 = np.zeros(shape=(n_h,1))
    W2 = np.random.randn(n_y,n_h)*0.01
    b2 = np.zeros(shape=(n_y,1))

    #利用断言函数判断一下数据结构是否正确
    assert(W1.shape == (n_h,n_x))
    assert(b1.shape == (n_h,1))
    assert(W2.shape == (n_y,n_h))
    assert(b2.shape == (n_y,1))

    parameters = {
      
        "W1":W1,
        "b1":b1,
        "W2":W2,
        "b2":b2
        }
    
    return parameters

#定义前向传播
def forward_propagation(X,parameters):
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    Z1 = np.dot(W1,X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2,A1) + b2
    A2 = sigmoid(Z2)

    assert(A2.shape == (1,X.shape[1]))

    cache = {
      
        "Z1":Z1,
        "A1":A1,
        "Z2":Z2,
        "A2":A2
        }
    
    return (A2,cache)

    
#定义代价函数
def compute_cost(A2,Y,parameters):
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]

    logprobs = np.multiply(np.log(A2),Y) + np.multiply((1-Y),np.log(1-A2))
    cost = -np.sum(logprobs) / m
    cost = float(np.squeeze(cost))

    assert(isinstance(cost,float))

    return cost

#定义后向传播
def backward_propagation(parameters,cache,X,Y):
    m = X.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]

    A1 = cache["A1"]
    A2 = cache["A2"]

    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2,A1.T)
    db2 = (1 / m) * np.sum(dZ2,axis=1,keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T,dZ2),1 - np.power(A1,2))
    dW1 = (1 / m) * np.dot(dZ1,X.T)
    db1 = (1 / m) * np.sum(dZ1,axis=1,keepdims=True)

    grads = {
      
        "dW1":dW1,
        "db1":db1,
        "dW2":dW2,
        "db2":db2
        }

    return grads

#更新参数
def update_parameters(parameters,grads,learning_rate=1.2):
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]

    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    parameters = {
      
        "W1":W1,
        "b1":b1,
        "W2":W2,
        "b2":b2
        }
    
    return parameters

#将上面的函数整合到一起
def nn_model(X,Y,num_iterations,print_cost=False):
    np.random.seed(3)
    
    n_x,n_h,n_y = layer_sizes(X,Y)

    parameters = initialize_parameters(n_x,n_h,n_y)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]

    for i in range(num_iterations):
        A2,cache = forward_propagation(X,parameters)
        cost = compute_cost(A2,Y,parameters)
        grads = backward_propagation(parameters,cache,X,Y)
        parameters = update_parameters(parameters,grads,learning_rate=0.5)

        if print_cost:
            if i % 1000 == 0:
                print("第",i,"次循环，成本为"+str(cost))

    return parameters

#定义预测函数
def predict(parameters,X):
     A2,cache = forward_propagation(X,parameters)
     predictions = np.round(A2)
     #round():返回浮点数x的四舍五入值
     return predictions

#计算参数
parameters = nn_model(X,Y,num_iterations=10000,print_cost=True)
'''
输出：
第 0 次循环，成本为0.6930480201239823
第 1000 次循环，成本为0.3098018601352803
第 2000 次循环，成本为0.2924326333792646
第 3000 次循环，成本为0.2833492852647411
第 4000 次循环，成本为0.27678077562979253
第 5000 次循环，成本为0.2634715508859307
第 6000 次循环，成本为0.24204413129940758
第 7000 次循环，成本为0.23552486626608762
第 8000 次循环，成本为0.23140964509854278
第 9000 次循环，成本为0.22846408048352362
'''

#计算准确率
predictions = predict(parameters,X)
print("准确率：%d" % float((np.dot(Y,predictions.T) +
                        np.dot(1-Y,1-predictions.T))
                       / float(Y.size) * 100) + "%")
#输出：准确率：90%

#画出边界
plot_decision_boundary(lambda x:predict(parameters,x.T),X,Y)
plt.title("Decision Boundary for hidden layer size"+str(4))
plt.show()
'''
决策边界绘制函数：plot_decision_boundary(model , X , y)
参考链接：https://blog.csdn.net/m0_46177963/article/details/107595826

lambda表达式：定义了一个匿名函数，即x为入口参数，predict(parameters,x.T)为函数体
'''

运行结果：

梯度计算公式参考（图片来源于吴恩达深度学习视频）：

planar_utils源代码：

import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model

def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)


def sigmoid(x):
    s = 1/(1+np.exp(-x))
    return s

def load_planar_dataset():
    np.random.seed(1)
    m = 400 # number of examples
    N = int(m/2) # number of points per class
    D = 2 # dimensionality
    X = np.zeros((m,D)) # data matrix where each row is a single example
    Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
    a = 4 # maximum ray of the flower

    for j in range(2):
        ix = range(N*j,N*(j+1))
        t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
        r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
        X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y

def load_extra_datasets():  
    N = 200
    noisy_circles = sklearn.datasets.make_circles(n_samples=N, factor=.5, noise=.3)
    noisy_moons = sklearn.datasets.make_moons(n_samples=N, noise=.2)
    blobs = sklearn.datasets.make_blobs(n_samples=N, random_state=5, n_features=2, centers=6)
    gaussian_quantiles = sklearn.datasets.make_gaussian_quantiles(mean=None, cov=0.5, n_samples=N, n_features=2, n_classes=2, shuffle=True, random_state=None)
    no_structure = np.random.rand(N, 2), np.random.rand(N, 2)

    return noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure

代码参考：【中文】【吴恩达课后编程作业】Course 1 - 神经网络和深度学习 - 第三周作业