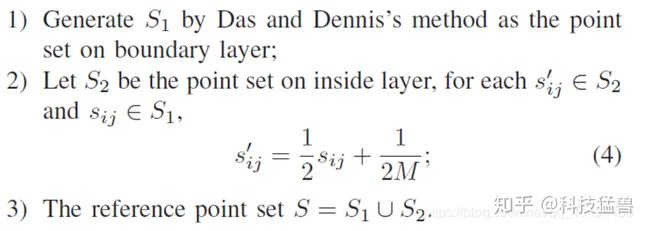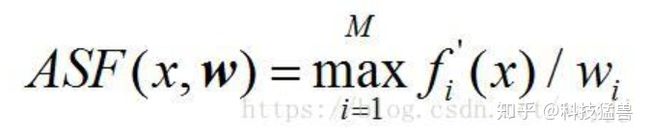遗传算法代码_遗传算法之NSGA-III原理分析和代码解读
因为multi-objective optimization已经被做烂了,现在学者们都在做many-objective optimization,也就是5个以上的目标函数(悄悄说一句,我觉得这个也要被做烂了)。此次我是用python复现的,这篇文章也主要以python代码讲解为主。
代码链接matlab和Python(需要软妹币):
多目标优化算法(四)NSGA3的代码(MATLAB)_套用nsga3程序代码matlab,nsga3matlab-机器学习代码类资源-CSDN下载download.csdn.net 多目标优化算法(四)NSGA3的代码(python3.6)_nsga-Ⅱ算法实现代码github,nsga3python-机器学习代码类资源-CSDN下载download.csdn.net摘要:NSGAIII的主要思路是在NSGAII的基础上,引入参考点机制,对于那些非支配并且接近参考点的种群个体进行保留。此次复现处理的优化问题是具有3到15个目标的DTLZ系列,仿真结果反应了NSGAIII良好的搜索帕累托最优解集的能力。
总体上来说,NSGAIII和NSGAII具有类似的框架,二者区别主要在于选择机制的改变,NSGAII主要靠拥挤度进行排序,其在高维目标空间显然作用不太明显,而NSGAIII对拥挤度排序进行了大刀阔斧的改编,通过引入广泛分布参考点来维持种群的多样性。
以下总结NSGAIII的第t代的步骤:
第一步将子代和父代结合:
主程序python代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 空间三维画图
from utils import uniformpoint,funfun,cal,GO,envselect,IGD
import copy
import random
#参数设置
N_GENERATIONS = 400 # 迭代次数
POP_SIZE = 100 # 种群大小
name = 'DTLZ1' # 测试函数选择,目前可供选择DTLZ1,DTLZ2,DTLZ3
M = 3 # 目标个数
t1 = 20 # 交叉参数t1
t2 = 20 # 变异参数t2
pc = 1 # 交叉概率
pm = 1 # 变异概率
#画图部分
if(M<=3):
fig = plt.figure()
ax = Axes3D(fig)
###################################################################################################################################################################
#产生一致性的参考点和随机初始化种群
Z,N = uniformpoint(POP_SIZE,M)#生成一致性的参考解
pop,popfun,PF,D = funfun(M,N,name)#生成初始种群及其适应度值,真实的PF,自变量个数
popfun = cal(pop,name,M,D)#计算适应度函数值
Zmin = np.array(np.min(popfun,0)).reshape(1,M)#求理想点
#ax.scatter(Z[:,0],Z[:,1],Z[:,2],c='r')
#ax.scatter(PF[:,0],PF[:,1],PF[:,2],c='b')
#迭代过程
for i in range(N_GENERATIONS):
print("第{name}次迭代".format(name=i))
matingpool=random.sample(range(N),N)
off = GO(pop[matingpool,:],t1,t2,pc,pm)#遗传算子,模拟二进制交叉和多项式变异
offfun = cal(off,name,M,D)#计算适应度函数
mixpop = copy.deepcopy(np.vstack((pop, off)))
Zmin = np.array(np.min(np.vstack((Zmin,offfun)),0)).reshape(1,M)#更新理想点
pop = envselect(mixpop,N,Z,Zmin,name,M,D)
popfun = cal(pop,name,M,D)
if(M<=3):
ax.cla()
type1 = ax.scatter(popfun[:,0],popfun[:,1],popfun[:,2],c='g')
plt.pause(0.00001)
# 绘制PF
if(M<=3):
type2 = ax.scatter(PF[:,0],PF[:,1],PF[:,2],c='r',marker = 'x',s=200)
plt.legend((type1, type2), (u'Non-dominated solution', u'PF'))
else:
fig1 = plt.figure()
plt.xlim([0,M])
for i in range(pop.shape[0]):
plt.plot(np.array(pop[i,:]))
plt.show()
#IGD
score = IGD(popfun,PF)
程序中pc是交叉概率,pm是变异概率。
1.将种群按照非支配层进行划分
将非支配层等级1到
非支配排序的python代码如下:
from scipy.special import comb
from itertools import combinations
import numpy as np
import copy
import math
def NDsort(mixpop,N,M):
nsort = N#排序个数
N,M = mixpop.shape[0],mixpop.shape[1]
Loc1=np.lexsort(mixpop[:,::-1].T)#loc1为新矩阵元素在旧矩阵中的位置,从第一列依次进行排序
mixpop2=mixpop[Loc1]
Loc2=Loc1.argsort()#loc2为旧矩阵元素在新矩阵中的位置
frontno=np.ones(N)*(np.inf)#初始化所有等级为np.inf
#frontno[0]=1#第一个元素一定是非支配的
maxfno=0#最高等级初始化为0
while (np.sum(frontno < np.inf) < min(nsort,N)):#被赋予等级的个体数目不超过要排序的个体数目
maxfno=maxfno+1
for i in range(N):
if (frontno[i] == np.inf):
dominated = 0
for j in range(i):
if (frontno[j] == maxfno):
m=0
flag=0
while (m=mixpop2[j,m]):
if(mixpop2[i,m]==mixpop2[j,m]):#相同的个体不构成支配关系
flag=flag+1
m=m+1
if (m>=M and flag < M):
dominated = 1
break
if dominated == 0:
frontno[i] = maxfno
frontno=frontno[Loc2]
return frontno,maxfno
frontno=np.ones(N)*(np.inf) #初始化所有等级为np.inf。
maxfno=0 #最高等级初始化为0。
N就是要排序的个数。
2.超平面上参考点的确定
NSGAIII使用一组预定义的参考点以确保解的多样性,这一组参考点可以结构化的方式定义,也可以用户根据自己的参考点。以下介绍一种产生结构化参考点的方法叫Das and Dennis’s method,此方法来源于田野老师对产生参考点方法的综述论文。其参考点在一个(M-1)维的超平面上,M是目标空间的维度,即优化目标的个数。如果我们将每个目标划分为
例如对于一个H=4的3目标问题,其参考点构成了一个三角形,根据公式可知其产生15个参考点,见图1所示。
一个用Das and Dennis’s method产生参考点坐标的过程这个产生方法其实有个bug,比如当目标函数数目比较大的时候(例如等于10),那么假设每个函数划分为10段,则会产生92378个参考点,这显然太大了,因此在复现NSGA-III里,我使用以下的参考点产生方法,其叫做Deb and Jain’s Method,此方法也可以在参考文献[3]里找到,其主要想法就是产生内层和外层两个参考点的超平面,这样可以减少参考点的产生,并保证参考点的广泛分布,其流程如下:
例如,一个三目标问题,每个目标函数划分为13份,利用此方法其只产生了210个参考点就保证了广泛分布性。如图3所示。
有人不禁会问这个内外层的
参考点生成的python代码如下:
from scipy.special import comb
from itertools import combinations
import numpy as np
import copy
import math
def uniformpoint(N,M):
H1=1
while (comb(H1+M-1,M-1)<=N):
H1=H1+1
H1=H1-1
W=np.array(list(combinations(range(H1+M-1),M-1)))-np.tile(np.array(list(range(M-1))),(int(comb(H1+M-1,M-1)),1))
W=(np.hstack((W,H1+np.zeros((W.shape[0],1))))-np.hstack((np.zeros((W.shape[0],1)),W)))/H1
if H10:
W2=np.array(list(combinations(range(H2+M-1),M-1)))-np.tile(np.array(list(range(M-1))),(int(comb(H2+M-1,M-1)),1))
W2=(np.hstack((W2,H2+np.zeros((W2.shape[0],1))))-np.hstack((np.zeros((W2.shape[0],1)),W2)))/H2
W2=W2/2+1/(2*M)
W=np.vstack((W,W2))#按列合并
W[W<1e-6]=1e-6
N=W.shape[0]
return W,N
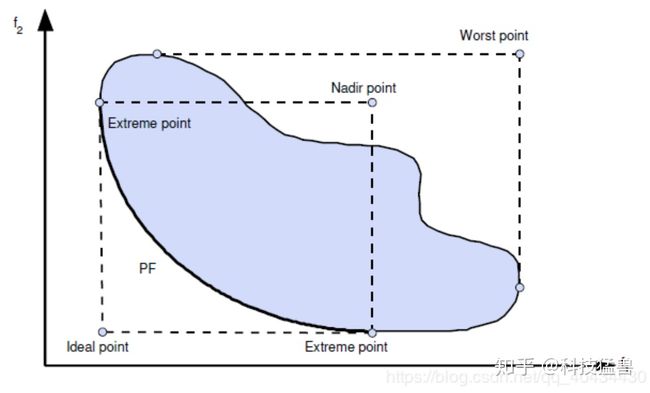
3.种群个体的自适应归一化
给出了一个三目标问题的截距计算过程,并从极值点生成超平面(图是未归一化的平面)以下给出这个过程的伪代码:
读到这里你可能没看懂上面是在说什么,那就再讲通俗一点:
种群成员的自适应归一化,在这个过程中较难理解的是极值点是如何得到的,下面简述大体步骤,重点分析极值点的产生。
以最小化为例,首先得到种群St中的所有个体在每一维目标上的最小值,构成当前种群的理想点,然后将所有个体的目标值,以及理想点以此理想点为参考作转换操作,这时理想点变为原点,个体的目标值为转换后的临时标准化目标值。然后计算每一维目标轴上的极值点,这M个极值点组成了M-1维的线性超平面,这时可以计算出各个目标方向上的截距。然后利用截距和临时的标准化目标值计算真正的标准化目标值:
其中ai为各维目标方向上的截距。针对三个目标问题,显示了计算截距然后从极点形成超平面的过程。
可能还没看懂,那就再举个更加通俗的例子:
还是上面的那个算法:
找极值点,求截距,归一化请密切注意下面的2个概念:理想点,极值点。
步骤2:Compute ideal point(计算理想点):即求解这一代种群所有目标的最小值。比如甲三个目标值是(2,3,5),乙的三个目标是(4,3,5),丙的三个目标是(3,3,4),那么 ideal point为(2,3,4)。
步骤3: Translate objectives(把所有个体的目标值减去 ideal point): 即甲三个目标值是(0,0,1),乙的三个目标是(2,0,1),丙的三个目标是(1,0,0)。
步骤4: Compute extreme points(计算极值点): 这是最难理解的一步。
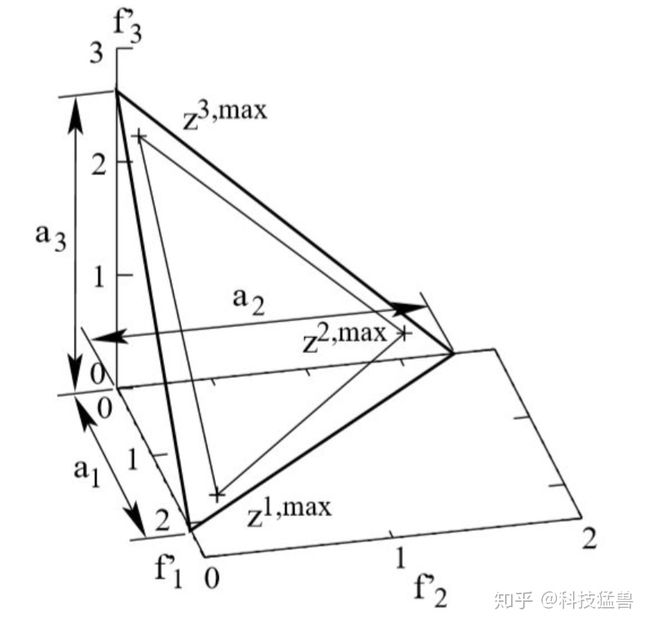
它的意思就是使得这个这方程最小的向量就是我们要找的极值点,这点比较难理解,我慢慢解释,拿三个目标的例子来说明,我们先看下图,这所谓的极值点指的啥?
其实就是图中的z1,max z2,max he z3,max三个点,它们各自和原点(即 ideal point)组成的三条线,这三条线就可以组成一个面,这个面和三个坐标轴的交点就是我们最终要求解的截距a1,a2和a3。找到截距后我们,用截距来按照下面的方程进行归一化:
归一化这个步骤本身很好理解。难理解的地方是怎么找到这个极值点。我们还是举三个目标的问题作为例子,我们初始化种群后,会得到很多个体,他们的目标值可能是(1,3,0.3),(2,6,0.3),(0.1,0.2,3)等等,如果有一些点如果在一个目标上的值很大,在另外两个目标上的值很小,这些点就更靠近这个坐标轴,这个就是所谓的 extreme points,目标就是找到在一个方向上值很大,另外两个目标值很小的点,三个目标的问题话对应我们可以找到三个这样的 extreme points。比如在ASF方程中,固定第一个坐标轴,(1,0.2,0.3)/(1,10e-6, 10e-6),这个时候最大的肯定是0.3这个方向,在固定第一个坐标轴时。我们在群体中找到另外两个目标中小的那个。比如(1,0.6,0.3)在ASF后变为0.6*10e6,(1,0.2,0.3)在ASF后变为0.3*10e6,(1,0.1,0.2)在ASF后变为0.2*10e6,这三个点那个作为extreme points最为合适,我想现在你肯定知道了,0.2*10e6是最小的,对应(1,0.1,0.2)是最合适的。
假设你得到的三个极值点分别是(-1, 1, 2), (2, 0, -3)和(5, 1, -2),下面开始求截距:
易知直线方程为2x-9y+3z+5=0
故截距为:-2.5,5/9和-5/3
最后使用上式归一化即可。
4.联系个体和参考点
这一步实际上就是找到每个个体距离最近的参考点的参考线,如图6所示。
种群个体与参考点之间的关系这一步算法的伪代码如下:
5.Niche-Preservation操作
根据步骤4,我们可以发现参考点和种群个体之间的关系可以是一对多,一对一或者没有对应。这一步我们要做的工作就是怎样通过这个关系选出剩余的K个解进入下一个种群。其伪代码如下:
循环K次:(j是参考点的索引)
1. 挑出
2. 找出
整个选择过程的python代码如下:
from scipy.special import comb
from itertools import combinations
import numpy as np
import copy
import math
#求两个向量矩阵的余弦值,x的列数等于y的列数
def pdist(x,y):
x0=x.shape[0]
y0=y.shape[0]
xmy=np.dot(x,y.T)#x乘以y
xm=np.array(np.sqrt(np.sum(x**2,1))).reshape(x0,1)
ym=np.array(np.sqrt(np.sum(y**2,1))).reshape(1,y0)
xmmym=np.dot(xm,ym)
cos = xmy/xmmym
return cos
def lastselection(popfun1,popfun2,K,Z,Zmin):
#选择最后一个front的解
popfun = copy.deepcopy(np.vstack((popfun1, popfun2)))-np.tile(Zmin,(popfun1.shape[0]+popfun2.shape[0],1))
N,M = popfun.shape[0],popfun.shape[1]
N1 = popfun1.shape[0]
N2 = popfun2.shape[0]
NZ = Z.shape[0]
#正则化
extreme = np.zeros(M)
w = np.zeros((M,M))+1e-6+np.eye(M)
for i in range(M):
extreme[i] = np.argmin(np.max(popfun/(np.tile(w[i,:],(N,1))),1))
#计算截距
extreme = extreme.astype(int)#python中数据类型转换一定要用astype
#temp = np.mat(popfun[extreme,:]).I
temp = np.linalg.pinv(np.mat(popfun[extreme,:]))
hyprtplane = np.array(np.dot(temp,np.ones((M,1))))
a = 1/hyprtplane
if np.sum(a==math.nan) != 0:
a = np.max(popfun,0)
np.array(a).reshape(M,1)#一维数组转二维数组
#a = a.T - Zmin
a=a.T
popfun = popfun/(np.tile(a,(N,1)))
##联系每一个解和对应向量
#计算每一个解最近的参考线的距离
cos = pdist(popfun,Z)
distance = np.tile(np.array(np.sqrt(np.sum(popfun**2,1))).reshape(N,1),(1,NZ))*np.sqrt(1-cos**2)
#联系每一个解和对应的向量
d = np.min(distance.T,0)
pi = np.argmin(distance.T,0)
#计算z关联的个数
rho = np.zeros(NZ)
for i in range(NZ):
rho[i] = np.sum(pi[:N1] == i)
#选出剩余的K个
choose = np.zeros(N2)
choose = choose.astype(bool)
zchoose = np.ones(NZ)
zchoose = zchoose.astype(bool)
while np.sum(choose) < K:
#选择最不拥挤的参考点
temp = np.ravel(np.array(np.where(zchoose == True)))
jmin = np.ravel(np.array(np.where(rho[temp] == np.min(rho[temp]))))
j = temp[jmin[np.random.randint(jmin.shape[0])]]
# I = np.ravel(np.array(np.where(choose == False)))
# I = np.ravel(np.array(np.where(pi[(I+N1)] == j)))
I = np.ravel(np.array(np.where(pi[N1:] == j)))
I = I[choose[I] == False]
if (I.shape[0] != 0):
if (rho[j] == 0):
s = np.argmin(d[N1+I])
else:
s = np.random.randint(I.shape[0])
choose[I[s]] = True
rho[j] = rho[j]+1
else:
zchoose[j] = False
return choose
def envselect(mixpop,N,Z,Zmin,name,M,D):
#非支配排序
mixpopfun = cal(mixpop,name,M,D)
frontno,maxfno = NDsort(mixpopfun,N,M)
Next = frontno < maxfno
#选择最后一个front的解
Last = np.ravel(np.array(np.where(frontno == maxfno)))
choose = lastselection(mixpopfun[Next,:],mixpopfun[Last,:],N-np.sum(Next),Z,Zmin)
Next[Last[choose]] = True
#生成下一代
pop = copy.deepcopy(mixpop[Next,:])
return pop
6.遗传算子
from scipy.special import comb
from itertools import combinations
import numpy as np
import copy
import math
def GO(pop,t1,t2,pc,pm):
pop1 = copy.deepcopy(pop[0:int(pop.shape[0]/2),:])
pop2 = copy.deepcopy(pop[(int(pop.shape[0]/2)):(int(pop.shape[0]/2)*2),:])
N,D = pop1.shape[0],pop1.shape[1]
#模拟二进制交叉
beta=np.zeros((N,D))
mu=np.random.random_sample([N,D])
beta[mu<=0.5]=(2*mu[mu<=0.5])**(1/(t1+1))
beta[mu>0.5]=(2-2*mu[mu>0.5])**(-1/(t1+1))
beta=beta*((-1)**(np.random.randint(2, size=(N,D))))
beta[np.random.random_sample([N,D])<0.5]=1
beta[np.tile(np.random.random_sample([N,1])>pc,(1,D))]=1
off = np.vstack(((pop1+pop2)/2+beta*(pop1-pop2)/2,(pop1+pop2)/2-beta*(pop1-pop2)/2))
#多项式变异
low=np.zeros((2*N,D))
up=np.ones((2*N,D))
site=np.random.random_sample([2*N,D]) < pm/D
mu = np.random.random_sample([2*N,D])
temp = site & (mu<=0.5)
off[offup]=up[off>up]
off[temp]=off[temp]+(up[temp]-low[temp])*((2*mu[temp]+(1-2*mu[temp])*((1-(off[temp]-low[temp])/(up[temp]-low[temp]))**(t2+1)))**(1/(t2+1))-1)
temp = site & (mu>0.5)
off[temp]=off[temp]+(up[temp]-low[temp])*(1-(2*(1-mu[temp])+2*(mu[temp]-0.5)*((1-(up[temp]-off[temp])/(up[temp]-low[temp]))**(t2+1)))**(1/(t2+1)))
return off
实验:
DTLZ1:
DTLZ2:
from scipy.special import comb
from itertools import combinations
import numpy as np
import copy
import math
def funfun(M,N,name):
#种群初始化
D=M+4#定义自变量个数为目标个数加4
low=np.zeros((1,D))
up=np.ones((1,D))
pop = np.tile(low,(N,1))+(np.tile(up,(N,1))-np.tile(low,(N,1)))*np.random.rand(N,D)
#计算PF
if name=='DTLZ1':
#g=np.transpose(np.mat(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))))
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(0.5*np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),pop[:,:(M-1)]))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.fliplr(pop[:,:(M-1)])))))
P,nouse = uniformpoint(N,M)
P=P/2
elif name=='DTLZ2':
#g=np.transpose(np.mat(np.sum((pop[:,(M-1):]-0.5)**2,1)))
g=np.array(np.sum((pop[:,(M-1):]-0.5)**2,1)).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
P,nouse = uniformpoint(N,M)
#P = P/np.tile(np.transpose(np.mat(np.sqrt(np.sum(P**2,1)))),(1,M))
P = P/np.tile(np.array(np.sqrt(np.sum(P**2,1))).reshape(P.shape[0],1),(1,M))
elif name=='DTLZ3':
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
P,nouse = uniformpoint(N,M)
#P = P/np.tile(np.transpose(np.mat(np.sqrt(np.sum(P**2,1)))),(1,M))
P = P/np.tile(np.array(np.sqrt(np.sum(P**2,1))).reshape(P.shape[0],1),(1,M))
return pop,popfun,P,D
def cal(pop,name,M,D):
N = pop.shape[0]
if name=='DTLZ1':
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(0.5*np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),pop[:,:(M-1)]))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.fliplr(pop[:,:(M-1)])))))
elif name=='DTLZ2':
g=np.array(np.sum((pop[:,(M-1):]-0.5)**2,1)).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
elif name=='DTLZ3':
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
return popfun
最后,为了方便理解,我列举了代码中一些变量的维度:
pop:(91,7)
popfun:(91,3)
off:(91,7)
offfun:(91,3)
mixpop:(181,7) = popfun+offfun
N=91
NZ=91
Z:(91,3)
Zmin:(1,3)
M=3:3个维度
D=7
frontno:(181,1)
cos:(127,91)
extreme=[61,41,26]
d:127
pi:(127,)
rho:(91,)
完整代码如下:
naga3.py:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 空间三维画图
from utils import uniformpoint,funfun,cal,GO,envselect,IGD
import copy
import random
#参数设置
N_GENERATIONS = 400 # 迭代次数
POP_SIZE = 100 # 种群大小
name = 'DTLZ1' # 测试函数选择,目前可供选择DTLZ1,DTLZ2,DTLZ3
M = 3 # 目标个数
t1 = 20 # 交叉参数t1
t2 = 20 # 变异参数t2
pc = 1 # 交叉概率
pm = 1 # 变异概率
#画图部分
if(M<=3):
fig = plt.figure()
ax = Axes3D(fig)
###################################################################################################################################################################
#产生一致性的参考点和随机初始化种群
Z,N = uniformpoint(POP_SIZE,M)#生成一致性的参考解
pop,popfun,PF,D = funfun(M,N,name)#生成初始种群及其适应度值,真实的PF,自变量个数
popfun = cal(pop,name,M,D)#计算适应度函数值
Zmin = np.array(np.min(popfun,0)).reshape(1,M)#求理想点
#ax.scatter(Z[:,0],Z[:,1],Z[:,2],c='r')
#ax.scatter(PF[:,0],PF[:,1],PF[:,2],c='b')
#迭代过程
for i in range(N_GENERATIONS):
print("Di {name}ci die dai".format(name=i))
matingpool=random.sample(range(N),N)
off = GO(pop[matingpool,:],t1,t2,pc,pm)#遗传算子,模拟二进制交叉和多项式变异
offfun = cal(off,name,M,D)#计算适应度函数
mixpop = copy.deepcopy(np.vstack((pop, off)))
Zmin = np.array(np.min(np.vstack((Zmin,offfun)),0)).reshape(1,M)#更新理想点
pop = envselect(mixpop,N,Z,Zmin,name,M,D)
popfun = cal(pop,name,M,D)
if(M<=3):
ax.cla()
type1 = ax.scatter(popfun[:,0],popfun[:,1],popfun[:,2],c='g')
plt.pause(0.00001)
# 绘制PF
if(M<=3):
type2 = ax.scatter(PF[:,0],PF[:,1],PF[:,2],c='r',marker = 'x',s=200)
plt.legend((type1, type2), (u'Non-dominated solution', u'PF'))
else:
fig1 = plt.figure()
plt.xlim([0,M])
for i in range(pop.shape[0]):
plt.plot(np.array(pop[i,:]))
plt.show()
#IGD
score = IGD(popfun,PF)utils.py:
from scipy.special import comb
from itertools import combinations
import numpy as np
import copy
import math
def uniformpoint(N,M):
H1=1
while (comb(H1+M-1,M-1)<=N):
H1=H1+1
H1=H1-1
W=np.array(list(combinations(range(H1+M-1),M-1)))-np.tile(np.array(list(range(M-1))),(int(comb(H1+M-1,M-1)),1))
W=(np.hstack((W,H1+np.zeros((W.shape[0],1))))-np.hstack((np.zeros((W.shape[0],1)),W)))/H1
if H10:
W2=np.array(list(combinations(range(H2+M-1),M-1)))-np.tile(np.array(list(range(M-1))),(int(comb(H2+M-1,M-1)),1))
W2=(np.hstack((W2,H2+np.zeros((W2.shape[0],1))))-np.hstack((np.zeros((W2.shape[0],1)),W2)))/H2
W2=W2/2+1/(2*M)
W=np.vstack((W,W2))#按列合并
W[W<1e-6]=1e-6
N=W.shape[0]
return W,N
def funfun(M,N,name):
#种群初始化
D=M+4#定义自变量个数为目标个数加4
low=np.zeros((1,D))
up=np.ones((1,D))
pop = np.tile(low,(N,1))+(np.tile(up,(N,1))-np.tile(low,(N,1)))*np.random.rand(N,D)
#pop是(N,D)
#计算PF
if name=='DTLZ1':
#g=np.transpose(np.mat(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))))
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
#每一个样本计算1个g值。
popfun=np.multiply(0.5*np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),pop[:,:(M-1)]))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.fliplr(pop[:,:(M-1)])))))
#popfun(N,M),N个样本,每个样本有M个函数值
P,nouse = uniformpoint(N,M)
P=P/2
elif name=='DTLZ2':
#g=np.transpose(np.mat(np.sum((pop[:,(M-1):]-0.5)**2,1)))
g=np.array(np.sum((pop[:,(M-1):]-0.5)**2,1)).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
P,nouse = uniformpoint(N,M)
#P = P/np.tile(np.transpose(np.mat(np.sqrt(np.sum(P**2,1)))),(1,M))
P = P/np.tile(np.array(np.sqrt(np.sum(P**2,1))).reshape(P.shape[0],1),(1,M))
elif name=='DTLZ3':
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
P,nouse = uniformpoint(N,M)
#P = P/np.tile(np.transpose(np.mat(np.sqrt(np.sum(P**2,1)))),(1,M))
P = P/np.tile(np.array(np.sqrt(np.sum(P**2,1))).reshape(P.shape[0],1),(1,M))
return pop,popfun,P,D
def cal(pop,name,M,D):
N = pop.shape[0]
if name=='DTLZ1':
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(0.5*np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),pop[:,:(M-1)]))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.fliplr(pop[:,:(M-1)])))))
elif name=='DTLZ2':
g=np.array(np.sum((pop[:,(M-1):]-0.5)**2,1)).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
elif name=='DTLZ3':
g=np.array(100*(D-M+1+np.sum(((pop[:,(M-1):]-0.5)**2-np.cos(20*np.pi*(pop[:,(M-1):]-0.5))),1))).reshape(N,1)
popfun=np.multiply(np.tile(1+g,(1,M)),(np.fliplr((np.hstack((np.ones((g.shape[0],1)),np.cos(pop[:,:(M-1)]*(np.pi/2))))).cumprod(1))))
popfun=np.multiply(popfun,(np.hstack((np.ones((g.shape[0],1)),1-np.sin(np.fliplr(pop[:,:(M-1)])*(np.pi/2))))))
return popfun
def GO(pop,t1,t2,pc,pm):
pop1 = copy.deepcopy(pop[0:int(pop.shape[0]/2),:])
pop2 = copy.deepcopy(pop[(int(pop.shape[0]/2)):(int(pop.shape[0]/2)*2),:])
N,D = pop1.shape[0],pop1.shape[1]
#模拟二进制交叉
beta=np.zeros((N,D))
mu=np.random.random_sample([N,D])
beta[mu<=0.5]=(2*mu[mu<=0.5])**(1/(t1+1))
beta[mu>0.5]=(2-2*mu[mu>0.5])**(-1/(t1+1))
beta=beta*((-1)**(np.random.randint(2, size=(N,D))))
beta[np.random.random_sample([N,D])<0.5]=1
beta[np.tile(np.random.random_sample([N,1])>pc,(1,D))]=1
off = np.vstack(((pop1+pop2)/2+beta*(pop1-pop2)/2,(pop1+pop2)/2-beta*(pop1-pop2)/2))
#多项式变异
low=np.zeros((2*N,D))
up=np.ones((2*N,D))
site=np.random.random_sample([2*N,D]) < pm/D
mu = np.random.random_sample([2*N,D])
temp = site & (mu<=0.5)
off[offup]=up[off>up]
off[temp]=off[temp]+(up[temp]-low[temp])*((2*mu[temp]+(1-2*mu[temp])*((1-(off[temp]-low[temp])/(up[temp]-low[temp]))**(t2+1)))**(1/(t2+1))-1)
temp = site & (mu>0.5)
off[temp]=off[temp]+(up[temp]-low[temp])*(1-(2*(1-mu[temp])+2*(mu[temp]-0.5)*((1-(up[temp]-off[temp])/(up[temp]-low[temp]))**(t2+1)))**(1/(t2+1)))
return off
def NDsort(mixpop,N,M):
nsort = N#排序个数
N,M = mixpop.shape[0],mixpop.shape[1]
Loc1=np.lexsort(mixpop[:,::-1].T)#loc1为新矩阵元素在旧矩阵中的位置,从第一列依次进行排序
mixpop2=mixpop[Loc1]
Loc2=Loc1.argsort()#loc2为旧矩阵元素在新矩阵中的位置
frontno=np.ones(N)*(np.inf)#初始化所有等级为np.inf
#frontno[0]=1#第一个元素一定是非支配的
maxfno=0#最高等级初始化为0
while (np.sum(frontno < np.inf) < min(nsort,N)):#被赋予等级的个体数目不超过要排序的个体数目
maxfno=maxfno+1
for i in range(N):
if (frontno[i] == np.inf):
dominated = 0
for j in range(i):
if (frontno[j] == maxfno):
m=0
flag=0
while (m=mixpop2[j,m]):
if(mixpop2[i,m]==mixpop2[j,m]):#相同的个体不构成支配关系
flag=flag+1
m=m+1
if (m>=M and flag < M):
dominated = 1
break
if dominated == 0:
frontno[i] = maxfno
frontno=frontno[Loc2]
return frontno,maxfno
#求两个向量矩阵的余弦值,x的列数等于y的列数
def pdist(x,y):
x0=x.shape[0]
y0=y.shape[0]
xmy=np.dot(x,y.T)#x乘以y
xm=np.array(np.sqrt(np.sum(x**2,1))).reshape(x0,1)
ym=np.array(np.sqrt(np.sum(y**2,1))).reshape(1,y0)
xmmym=np.dot(xm,ym)
cos = xmy/xmmym
return cos
def lastselection(popfun1,popfun2,K,Z,Zmin):
#选择最后一个front的解
popfun = copy.deepcopy(np.vstack((popfun1, popfun2)))-np.tile(Zmin,(popfun1.shape[0]+popfun2.shape[0],1))
N,M = popfun.shape[0],popfun.shape[1]
N1 = popfun1.shape[0]
N2 = popfun2.shape[0]
NZ = Z.shape[0]
#正则化
extreme = np.zeros(M)
w = np.zeros((M,M))+1e-6+np.eye(M)
for i in range(M):
extreme[i] = np.argmin(np.max(popfun/(np.tile(w[i,:],(N,1))),1))
#计算截距
extreme = extreme.astype(int)#python中数据类型转换一定要用astype
#temp = np.mat(popfun[extreme,:]).I
temp = np.linalg.pinv(np.mat(popfun[extreme,:]))
hyprtplane = np.array(np.dot(temp,np.ones((M,1))))
a = 1/hyprtplane
if np.sum(a==math.nan) != 0:
a = np.max(popfun,0)
np.array(a).reshape(M,1)#一维数组转二维数组
#a = a.T - Zmin
a=a.T
popfun = popfun/(np.tile(a,(N,1)))
##联系每一个解和对应向量
#计算每一个解最近的参考线的距离
cos = pdist(popfun,Z)
distance = np.tile(np.array(np.sqrt(np.sum(popfun**2,1))).reshape(N,1),(1,NZ))*np.sqrt(1-cos**2)
#联系每一个解和对应的向量
d = np.min(distance.T,0)
pi = np.argmin(distance.T,0)
#计算z关联的个数
rho = np.zeros(NZ)
for i in range(NZ):
rho[i] = np.sum(pi[:N1] == i)
#选出剩余的K个
choose = np.zeros(N2)
choose = choose.astype(bool)
zchoose = np.ones(NZ)
zchoose = zchoose.astype(bool)
while np.sum(choose) < K:
#选择最不拥挤的参考点
temp = np.ravel(np.array(np.where(zchoose == True)))
jmin = np.ravel(np.array(np.where(rho[temp] == np.min(rho[temp]))))
j = temp[jmin[np.random.randint(jmin.shape[0])]]
# I = np.ravel(np.array(np.where(choose == False)))
# I = np.ravel(np.array(np.where(pi[(I+N1)] == j)))
I = np.ravel(np.array(np.where(pi[N1:] == j)))
I = I[choose[I] == False]
if (I.shape[0] != 0):
if (rho[j] == 0):
s = np.argmin(d[N1+I])
else:
s = np.random.randint(I.shape[0])
choose[I[s]] = True
rho[j] = rho[j]+1
else:
zchoose[j] = False
return choose
def envselect(mixpop,N,Z,Zmin,name,M,D):
#非支配排序
mixpopfun = cal(mixpop,name,M,D)
frontno,maxfno = NDsort(mixpopfun,N,M)
Next = frontno < maxfno
#选择最后一个front的解
Last = np.ravel(np.array(np.where(frontno == maxfno)))
choose = lastselection(mixpopfun[Next,:],mixpopfun[Last,:],N-np.sum(Next),Z,Zmin)
Next[Last[choose]] = True
#生成下一代
pop = copy.deepcopy(mixpop[Next,:])
return pop
def EuclideanDistances(A, B):
BT = B.transpose()
# vecProd = A * BT
vecProd = np.dot(A,BT)
# print(vecProd)
SqA = A**2
# print(SqA)
sumSqA = np.matrix(np.sum(SqA, axis=1))
sumSqAEx = np.tile(sumSqA.transpose(), (1, vecProd.shape[1]))
# print(sumSqAEx)
SqB = B**2
sumSqB = np.sum(SqB, axis=1)
sumSqBEx = np.tile(sumSqB, (vecProd.shape[0], 1))
SqED = sumSqBEx + sumSqAEx - 2*vecProd
SqED[SqED<0]=0.0
ED = np.sqrt(SqED)
return ED
def IGD(popfun,PF):
distance = np.min(EuclideanDistances(PF,popfun),1)
score = np.mean(distance)
return score 参考链接:
多目标优化算法(四)NSGA3(NSGAIII)论文复现以及matlab和python的代码_晓风-CSDN博客_nsga3blog.csdn.net