第十届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第十届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第一题 平方序列（5 分）

【问题描述】

小明想找到两个正整数 X 和 Y，满足

• 2019 < X < Y;

• 2019^2 , X^2 , Y^2

组成等差数列。 请你求出在所有可能的解中，X + Y 的最小值是多少？

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

• 答案：7020

思路：暴力枚举

这是一道填空题，优先尝试小规模暴力枚举，先限制枚举最大范围为10000，如果出来的结果小于10000，则这个结果是正确的

代码实现

#include
#include
using namespace std; 
 
int main(){
     
	int a1=2019*2019,a2,a3,x,y,t;
	int min=100000;
	for(int i=2020;i<10000;i++){
     
		for(int j=i+1;j<10000;j++){
     
			a2=i*i,a3=j*j;
			if(i*i-a1==a3-a2){
     
				t=i+j;
				if(t<min){
     
					x=i;
					y=j;
					min=t;
				}
			}
		}
	}
	cout<<"min="<<min<<":x="<<x<<":y="<<y;
	return 0;
} 

• 计算结果min=7020，小于10000，任意y大于10000的解都会导致min>10000，故7020是满足要求的最小和

第二题 质数拆分（5 分）

【问题描述】

​ 将 2019 拆分为若干个两两不同的质数之和，一共有多少种不同的方法？ 注意交换顺序视为同一种方法，例如 2 + 2017 = 2019 与 2017 + 2 = 2019 视为同一种方法。

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：1

思路：暴力枚举

1. 计算2~2019内的所有素数
2. 暴力枚举所有素数两两组合，保证前一个素数小于后一个素数以防重复
3. 按照prim[i]+prim[j]==2019的条件筛选病累加适合的组合数

代码实现

#include
#include
using namespace std;

int prim[2019];
int num=0;

//获取2~2019所有质数 
void get_prim(int n){
     
	prim[0]=2;
	prim[1]=3;
	if(n<2)	return;
	if(n==2){
     
		num=1;
		return;
	}
	if(n==3){
     
		num=2;
		return;
	}
	num=2;
	int j;
	for(int i=5;i<=n;i+=2){
     
		for(j=1;j<num&&i%prim[j];j++);
		if(j==num&&i%prim[j-1]) prim[num++]=i;
	}
} 

int main(){
     
	get_prim(2019);
	for(int i=0;i<num;i++){
     
		printf("%-5d",prim[i]);
	}
	cout<<endl<<"共"<<num<<"个质数"<<endl;
	int ans=0;
	//暴力枚举所有质数 
	for(int i=0;i<num;i++){
     
		for(int j=i+1;j<num;j++){
     
			if(prim[i]+prim[j]==2019){
     
				ans++;
				cout<<"第"<<ans<<"个方案:"<<prim[i]<<"+"<<prim[j]<<"=="<<"2019"<<endl; 
			}
		}
	}
	cout<<"共计"<<ans<<"个方案"<<endl; 
	return 0;
}

第三题 拼接（10 分）

【问题描述】 小明要把一根木头切成两段，然后拼接成一个直角。 如下图所示，他把中间部分分成了 n × n 的小正方形，他标记了每个小正方 形属于左边还是右边。然后沿两边的分界线将木头切断，将右边旋转向上后拼 接在一起。

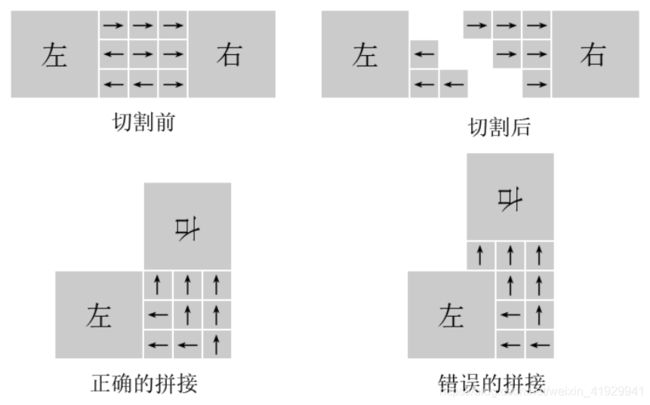
要求每个小正方形都正好属于左边或右边，而且同一边的必须是连通的。 在拼接时，拼接的部位必须保持在原来大正方形里面。 请问，对于 7 × 7 的小正方形，有多少种合法的划分小正方形的方式。

【答案提交】 这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

• 答案：14种

思路：找对称轴

1. 观察7x7的矩阵，所有符合要求的组合都关于x=y轴对称
2. 要满足关于x=y对称的要求，必须关于右下轴对称的边界延伸
3. 按照以上要求，延伸填写下表可以得到13种方案，另外还有一种方案是全都不选，共14种

7	8	9	10	11	12	13
6	7	8	9	10	11	12
5	6	7	8	9	10	11
4	5	6	7	8	9	10
3	4	5	6	7	8	9
2	3	4	5	6	7	8
1	2	3	4	5	6	7

第四题 求值（10 分）

【问题描述】

学习了约数后，小明对于约数很好奇，他发现，给定一个正整数 t，总是可 以找到含有 t 个约数的整数。小明对于含有 t 个约数的最小数非常感兴趣，并 把它定义为 S t 。 例如 S 1 = 1, S 2 = 2, S 3 = 4, S 4 = 6，· · · 。 现在小明想知道，当 t = 100 时，S t 是多少？即 S 100 是多少？

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

• 答案：45360

思路：暴力枚举

从1开始枚举，每次用ans计数记录约数个数（取模得0就是约数），直到第一个ans==100

代码实现

#include
using namespace std;

int main(){
     
	int num=2,ans;
	while(ans!=100){
     	//只有约数刚好是100个的时候跳出来 
		ans=2;			//除了1以外1和它本身1定是约数 
        num++;
		for(int j=2;j<num;j++)
			if(num%j==0) ans++;	//找到一个约数 
	} 
	cout<<num;
	return 0;
} 

第五题 路径计数（15 分）

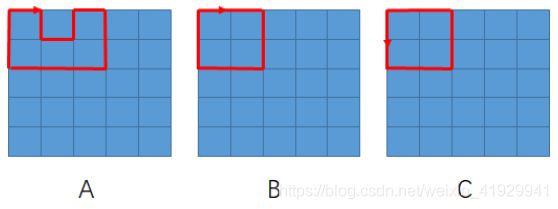
【问题描述】 从一个 5x5 的方格矩阵的左上角出发，沿着方格的边走，满足以下条件的 路线有多少种？

• 总长度不超过 12；

• 最后回到左上角；

• 路线不自交；

• 不走出 5x5 的方格矩阵范围之外。

如下图所示，ABC 是三种合法的路线。注意 B 和 C 由于方向不同，所以 视为不同的路线。

【答案提交】 这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

• 答案：208

思路：DFS+剪枝

1. 用8x8的数组表示地图，0和7表示越界了
2. 每个点有四个方向可以走，即4个分支
3. 递归出口：回到（1,1）点，此时返回1即可
4. 剪枝：走了13步时剪掉该分枝（返回0），走出了边界(返回0），要保证路线不相交就是保证不走重复的点（点走过了直接返回1）
5. 用1表示走过了，0表示没走过

代码实现

#include
#include
using namespace std;

int map[8][8]={
     0};

int dfs(int x,int y,int step){
     
	if(step>12)	return 0;								//走了超过12步 
	if(x==1&&y==1&&map[1][1])	return 1;				//走到终点 
	if(x==0||x==7||y==0||y==7||map[x][y]) return 0;		//越界或者走过了都剪枝
	map[x][y]=1;										//走向当前这格 
	int ans=0;				
	ans+=dfs(x+1,y,step+1);								//向右走一步 
	ans+=dfs(x,y+1,step+1);								//向下走一步 
	ans+=dfs(x-1,y,step+1);								//向左走一步	 
	ans+=dfs(x,y-1,step+1); 							//向上走一步
	map[x][y]=0;										//回溯 
	return ans; 
} 

int main(){
     
	cout<<dfs(1,1,0);
	return 0; 
}

第六题 最优包含（15分）

时间限制: 1.0s 内存限制: 256.0MB

【问题描述】 我们称一个字符串 S 包含字符串 T 是指 T 是 S 的一个子序列，即可以从字符串 S 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 T 完全一样。 给定两个字符串 S 和 T，请问最少修改 S 中的多少个字符，能使 S 包含 T ？

【输入格式】 输入两行，每行一个字符串。第一行的字符串为 S，第二行的字符串为 T。 两个字符串均非空而且只包含大写英文字母。

【输出格式】 输出一个整数，表示答案。

【样例输入】

ABCDEABCD

XAABZ

【样例输出】

3

【评测用例规模与约定】

对于 20% 的评测用例，1 ≤ |T| ≤ |S | ≤ 20； 对于 40% 的评测用例，1 ≤ |T| ≤ |S | ≤ 100； 对于所有评测用例，1 ≤ |T| ≤ |S | ≤ 1000。

思路：动态规划

1. dp[i] [j]表示s字符串的前j个子序列包含t字符串的前i个子序列最少需要修改的字符数
2. 字符串S每向后延伸一位，都有3种情况
   a.选择前面已经匹配的了，即dp[i] [j]=dp[i] [j-1]
   b.1.s当前这一位正好和t的第i位匹配了，此时选择当前位置与位置匹配dp[i] [j]=dp[i-1] [j-1]
   b.2.s当前这一位和t的第i位不匹配，此时选择当前位置与i位置字符，即dp[i] [j]=1+dp[i-1] [j-1]
3. 状态转移方程d[i] [j]=min(d[i] [j-1],s[j]==t[i]?d[i-1] [j-1]:(1+d[i-1] [j-1]))
4. 初始状态：dp[i] [j]=0
5. d[n-1] [m-1]即为所求

• 该题类似最短编辑距离

代码实现

#include
#include 
using namespace std;

char S[1001],T[1001];
int **dp;

int main(){
     
	cin>>S+1>>T+1;	//0下标不用
	int n,m;		//n是S字符个数，m是T字符个数 
	for(n=1;S[n]!='\0';n++);	//计算字符串S长度 
	for(m=1;T[m]!='\0';m++);	//计算字符串T长度 
	dp=new int*[n];
	for(int i=0;i<m;i++) dp[i]=new int[n];
	//1.确定初始状态 
	for(int i=0;i<m;i++)
		for(int j=0;j<n;j++) 
			dp[i][j]=0;
	//2.用状态转移方程填表
	int t;
	for(int i=1;i<m;i++){
     
		for(int j=i;j<n;j++){
     
			if(T[i]==S[j]) t=dp[i-1][j-1];		//两字符相同
			else  t=1+dp[i-1][j-1];				//两字符不相同
			if(j>i&&dp[i][j-1]<t) t=dp[i][j-1];	//前一个位置的匹配更小
			dp[i][j]=t;							//把最小的赋给dp[i][j]  
		}
	} 
//	for(int i=1;i
//		for(int j=1;j
//			cout<
//		}
//		cout<
//	}
	//3.输出结果 
	cout<<dp[m-1][n-1];
	return 0; 
}

第七题 排列数（20 分）

时间限制: 3.0s 内存限制: 256.0MB

【问题描述】

在一个排列中，一个折点是指排列中的一个元素，它同时小于两边的元素，或者同时大于两边的元素。

对于一个 1 ∼ n 的排列，如果可以将这个排列中包含 t 个折点，则它称为一个 t + 1 单调序列。

例如，排列 (1, 4, 2, 3) 是一个 3 单调序列，其中 4 和 2 都是折点。

给定 n 和 k，请问 1 ∼ n 的所有排列中有多少个 k 单调队列？

【输入格式】

输入一行包含两个整数 n, k。

【输出格式】

输出一个整数，表示答案。答案可能很大，你只需要输出满足条件的排列数量除以 123456 的余数即可。

【样例输入】

4 2

【样例输出】

12

【评测用例规模与约定】

对于 20% 的评测用例，1 ≤ k ≤ n ≤ 10；

对于 40% 的评测用例，1 ≤ k ≤ n ≤ 20；

对于 60% 的评测用例，1 ≤ k ≤ n ≤ 100；

对于所有评测用例，1 ≤ k ≤ n ≤ 500。

第八题 解谜游戏 (20分)

时间限制: 1.0s 内存限制: 256.0MB

【问题描述】

小明正在玩一款解谜游戏。谜题由 24 根塑料棒组成，其中黄色塑料棒 4 根，红色 8 根，绿色 12 根 (后面用 Y 表示黄色、R 表示红色、G 表示绿色)。 初始时这些塑料棒排成三圈，如上图所示，外圈 12 根，中圈 8 根，内圈 4 根。

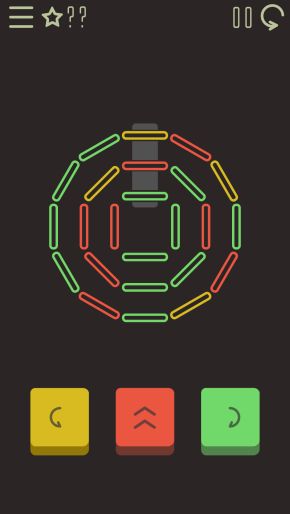
小明可以进行三种操作：

1. 将三圈塑料棒都顺时针旋转一个单位。例如当前外圈从 0 点位置开始 顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那 么顺时针旋转一次之后，外圈、中圈、内圈依次变为：GYRYGRYGRGGG、 YRGRGGRR 和 RGGG。
2. 将三圈塑料棒都逆时针旋转一个单位。例如当前外圈从 0 点位置开始 顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那 么逆时针旋转一次之后，外圈、中圈、内圈依次变为：RYGRYGRGGGGY、 GRGGRRYR 和 GGRG
3. 将三圈 0 点位置的塑料棒做一个轮换。具体来说：外圈 0 点塑料棒 移动到内圈 0 点，内圈 0 点移动到中圈 0 点，中圈 0 点移动到外圈 0 点。 例如当前外圈从 0 点位置开始顺时针依次是 YRYGRYGRGGGG，中圈是 RGRGGRRY，内圈是 GGGR。那么轮换一次之后，外圈、中圈、内圈依次变 为：RRYGRYGRGGGG、GGRGGRRY 和 YGGR。

小明的目标是把所有绿色移动到外圈、所有红色移动中圈、所有黄色移动 到内圈。给定初始状态，请你判断小明是否可以达成目标？

【输入格式】

第一行包含一个整数 T，代表询问的组数。(1 ≤ T ≤ 100)。 每组询问包含 3 行： 第一行包含 12 个大写字母，代表外圈从 0 点位置开始顺时针每个塑料棒 的颜色。 第二行包含 8 个大写字母，代表中圈从 0 点位置开始顺时针每个塑料棒的 颜色。 第三行包含 4 个大写字母，代表内圈从 0 点位置开始顺时针每个塑料棒的 颜色。

【输出格式】

对于每组询问，输出一行 YES 或者 NO，代表小明是否可以达成目标。

【样例输入】

2

GYGGGGGGGGGG

RGRRRRRR

YRYY

YGGGRRRRGGGY

YGGGRRRR

YGGG

【样例输出】

YES NO

思路：模运算

1. 以4为模，无论怎么操作，三行中所有的原本对4取模相等的位置在任意操作以后再对4取模仍相等
2. 基于1的分析，无论怎样操作所有的黄色最终要移动到内圈，即所有的黄色位置对4取模都不能相同
3. 基于1的分析，无论怎样操作，最终所有的红色都要在中圈，即所有的红色位置对4取模都要刚好有2个相等
4. 基于1的分析，无论怎样操作，最终所有的绿色都要在外圈，即所有的绿色位置对4取模都要刚好有3个相等 
5. 基于2.3.4分析，得出判断条件，用count[3] [4]记录三种颜色对4取模的结果个数,第一行表示黄色，第二行表示红色，第三行表示绿色，如果coutn[0] [i]==1，count[1] [i]==2,count[2] [i]==3则可能可以转移成，否则一定不行 
6. 转移成功分析：假设除了0方向以外其余的位置都成功归位了，而有0方向有两层换位了，通过保持黄色全正确，此时必是红绿异位，此时顺时针选择2x4次，上移1次再顺时针旋转4x4次，上移2次就可归位，故可行；而当非0方向异位的时候，只要满足5的条件都可以转移成除了0方向以外其余的位置都成功归位了的情况 

代码实现

#include
#include
using namespace std;

bool *result;		//用于记录结果 
int count[3][4];

bool judge(char out[],char mid[],char in[]){
     
	for(int i=0;i<3;i++)
		for(int j=0;j<4;j++)
			count[i][j]=0;
	for(int i=0;i<12;i++){
     						//外圈统计 
		if(out[i]=='Y') count[0][i%4]++;		//黄色 
		if(out[i]=='R') count[1][i%4]++;		//红色
		if(out[i]=='G') count[2][i%4]++;		//绿色 
	}
	for(int i=0;i<8;i++){
     						//中圈统计 
		if(mid[i]=='Y') count[0][i%4]++;		//黄色 
		if(mid[i]=='R') count[1][i%4]++;		//红色
		if(mid[i]=='G') count[2][i%4]++;		//绿色 
	} 
	for(int i=0;i<4;i++){
     						//内圈统计 
		if(in[i]=='Y') count[0][i%4]++;			//黄色 
		if(in[i]=='R') count[1][i%4]++;			//红色
		if(in[i]=='G') count[2][i%4]++;			//绿色 
	} 
	for(int i=0;i<4;i++){
     						//按条件5判断 
		if(count[0][i]!=1) return false;
		if(count[1][i]!=2) return false;
		if(count[2][i]!=3) return false;
	} 
	return true;
}

int main(){
     
	char out[12],mid[8],in[4];
	int n;
	//1.输入组数 
	cin>>n;
	result=new bool[n];
	//2.输入组判断一组 
	for(int i=0;i<n;i++){
     
		cin>>out>>mid>>in;
		result[i]=judge(out,mid,in);
	}
	//3.输出结果 
	for(int i=0;i<n;i++){
     
		if(result[i]) cout<<"YES";
		else cout<<"NO"; 
		if(i!=n-1) cout<<endl;
	}
	return 0;
}

第九题 第八大奇迹（25 分）

时间限制: 1.0s 内存限制: 256.0MB

【问题描述】

在一条 R 河流域，繁衍着一个古老的名族 Z。他们世代沿河而居，也在河边发展出了璀璨的文明。Z 族在 R 河沿岸修建了很多建筑，最近，他们热衷攀比起来。他们总是在比谁的建筑建得最奇特。幸好 Z 族人对奇特的理解都差不多，他们很快给每栋建筑都打了分，这样评选谁最奇特就轻而易举了。于是，根据分值，大家很快评出了最奇特的建筑，称为大奇迹。后来他们又陆续评选了第二奇特、第二奇特、……、第七奇特的建筑，依次称为第二大奇迹、第三大奇迹、……、第七大奇迹。

最近，他们开始评选第八奇特的建筑，准备命名为第八大奇迹。

在评选中，他们遇到了一些问题。

首先，Z 族一直在发展，有的建筑被拆除又建了新的建筑，新建筑的奇特值和原建筑不一样，这使得评选不那么容易了。

其次，Z 族的每个人所生活的范围可能不一样，他们见过的建筑并不是所有的建筑，他们坚持他们自己所看到的第八奇特的建筑就是第八大奇迹。

Z 族首领最近很头疼这个问题，他害怕因为意见不一致导致 Z 族发生分歧。他找到你，他想先了解一下，民众自己认为的奇迹是怎样的。

现在告诉在 R 河周边的建筑的变化情况，以及在变化过程中一些人的生活范围，请编程求出每个人认为的第八大奇迹的奇特值是多少。

【输入格式】

输入的第一行包含两个整数 L, N，分别表示河流的长度和要你处理的信息的数量。开始时河流沿岸没有建筑，或者说所有的奇特值为 0。接下来 N 行，每行一条你要处理的信息。

如果信息为 C p x，表示流域中第 p 个位置 (1 ≤ p ≤ L) 建立了一个建筑，其奇特值为 x。如果这个位置原来有建筑，原来的建筑会被拆除。

如果信息为 Q a b，表示有个人生活的范围是河流的第 a 到 b 个位置（包含 a 和 b，a ≤ b），这时你要算出这个区间的第八大奇迹的奇特值，并输出。如果找不到第八大奇迹，输出 0。

【输出格式】

对于每个为 Q 的信息，你需要输出一个整数，表示区间中第八大奇迹的奇特值。

【样例输入】

10 15

C 1 10

C 2 20

C 3 30

C 4 40

C 5 50

C 6 60

C 7 70

C 8 80

C 9 90

C 10 100

Q 1 2

Q 1 10

Q 1 8

C 10 1

Q 1 10

【样例输出】

0

30

10

20

【评测用例规模与约定】

对于 20% 的评测用例，1 ≤ L ≤ 1000, 1 ≤ N ≤ 1000。

对于 40% 的评测用例，1 ≤ L ≤ 10000, 1 ≤ N ≤ 10000。

对于 100% 的评测用例，1 ≤ L ≤ 100000，1 ≤ N ≤ 100000。所有奇特值为不超过 10^9 的非负整数。

思路：快速排序找第K大数

1. 用rivers[L]记录河流上的建筑情况，每个位置只需记录奇特值即可
2. 对于每个Q a b先判断在[a,b]范围内是否有8个或8个以上的建筑，如果不足8个建筑，直接记录结果0
3. 对于[a,b]范围内有8个或者8个以上的建筑的情况，利用快速排序，找出rivers[a]到rivers[b]范围内第8大的数并将其返回
4. 将第i个Q找到的答案放入数组result[i]中，待输入完成时，将result按顺序输出
5. 为识别resunt的结束位，使用n对Q计数

代码实现

#include
#include
#define MAX 100000
using namespace std;

int river[MAX+1]={
     -1};		//记录河流上的建筑 
int temp[MAX+1];			//快速排序复用的暂存数组 
int count;					//快速排序需要处理的数组长度 

//快速排序的划分算法 
int partation(int l,int r){
     
	int mid=(l+r)/2;		//确定枢轴
	int p=temp[mid];
	temp[mid]=temp[l];		//交换中间和第一位
	while(l<r){
     
		while(l<r&&temp[r]<=p) r--;
		if(l<r) temp[l++]=temp[r];
		while(l<r&&temp[l]>=p) l++;
		if(l<r) temp[r--]=temp[l];
	}
	temp[l]=p;
	return l;
} 

//快速排序降序排序找到river[a，b]中第八大的数 
int find_eight(int a,int b){
      
	int p = partation(a,b);
	if(p==8) return temp[8];			//刚好第8大的数 
	if(p<8) return find_eight(p+1,b);	//比第八个还大的数，往后找 
	else 	return find_eight(a,p-1);  	//比第八个还小的数，往前找 
} 

int main(){
     
	int L,N,index,a,b,n=0;
	cin>>L>>N;
	int result[N];
	char c;
	for(int i=0;i<N;i++){
     
		cin>>c;
		if(c=='C'){
     					//建造建造 
			cin>>index;
			cin>>river[index];
		}else{
     						//居住用户
			cin>>a>>b;
			count=0;
			for(int j=a;j<=b;j++)	//复制范围内所有奇迹分 
				if(river[j]>=0) temp[++count]=river[j];
			if(count<8) result[n++]=0;
			else result[n++]=find_eight(1,count);
		}
	}
	for(int i=0;i<n;i++){
     
		cout<<result[i];
		if(i!=n-1) cout<<endl;
	}
	return 0;
} 

第十题 燃烧权杖（25 分）

时间限制: 1.0s 内存限制: 256.0MB

【问题描述】

小 C 最近迷上了一款游戏。现在，在游戏中，小 C 有一个英雄，生命值为x；敌人也有一个英雄，生命值为 y。除此以外，还有 k 个士兵，生命值分别为a*1、a2、……、a**k。

现在小 C 打算使用一个叫做“燃烧权杖”的技能。“燃烧权杖”会每次等概率随机选择一个活着的角色（英雄或士兵），扣减其 10 点生命值，然后如果该角色的生命值小于或等于 0，则该角色死亡，不会再被“燃烧权杖”选中。“燃烧权杖”会重复做上述操作，直至任意一名英雄死亡。

小 C 想知道使用“燃烧权杖”后敌方英雄死亡（即，小 C 的英雄存活）的概率。为了避免精度误差，你只需要输出答案模一个质数 p 的结果，具体见输出格式。

【输入格式】

输入包含多组数据。

输入第一行包含一个正整数 T，表示数据组数。

接下来 T 组，每组数据第一行包含四个非负整数 x、y、p、k，分别表示小C 的英雄的生命值、敌方英雄的生命值，模数和士兵个数。

第二行包含 k 个正整数 a1、a2、……、a**k，分别表示每个士兵的生命值。

【输出格式】

对于每组数据，输出一行一个非负整数，表示答案模质数 p 的余数。

可以证明，答案一定为有理数。设答案为 a/b（a 和 b 为互质的正整数），你输出的数为 x，则你需要保证 a 与 bx 模 p 同余；也即，x = (a · b 1) mod p，其中 b 1 表示 b 模 p 的逆元， mod 为取模运算。

【样例输入】

6

1 10 101 0

100 1 101 0

50 30 4903 2

1 1

987 654 233 1

321

1000000000 999999999 233 3

1 2 3

1000000000 999999999 3 3

1 2 3

【样例输出】

51

37

1035

118

117

2

【样例说明】

对于第一组数据，所求概率即为“燃烧权杖”第一次就扣减敌方英雄 10 点

生命值的概率，即 1/2。2 × 51 模 101 余 1。

对于第二组数据，答案为 1023/1024，1024 × 37 与 1023 模 101 同余。

对于第三组数据，答案为 99/128。

【评测用例规模与约定】

对于 10% 的评测用例，x, y, a1, · · · , a**k ≤ 10。

对于 20% 的评测用例，x, y, a1, · · · , a**k ≤ 100。

对于 50% 的评测用例，x, y, a1, · · · , a**k ≤ 1000。

另有 10% 的评测用例，p = 3。

另有 20% 的评测用例，p ≤ 100。

对于全部评测用例，1 ≤ x, y, a1, · · · , a**k ≤ 109，3 ≤ p ≤ 10000 且 p 为质数，

0 ≤ k ≤ 10。

思路：无视小兵

1. 对于燃烧权杖的英雄间的博弈，与小兵没有关系，如果随机机制没有打中英雄，直接无视掉这次统计对最后结果没有影响，因为整个事件敌方英雄死亡和我方英雄死亡是一个对立事件，打中小兵全当没有发生无任何影响，这对博弈双方的形势没有任何改变
2. 概率的计算：由于事件胜负只关于打中对方英雄和自己，故每次统计都是1/2概率打中对方或1/2打中自己，由于对方英雄死亡和己方死亡是对立事件，整个计算有两种思路 a.计算己方死亡取补集 b.计算对方英雄死亡的概率
3. 具体计算思想：一开始连续击中对方英雄+一次击中自己其余击中敌方英雄+二次击中自己其余击中敌方英雄…
4. 概率公式：假设我方英雄击中j次死亡，敌方英雄击中i次死亡，P=sum(group(i-1,k-1)*(1/2)^k)(i<=k<=i+j-1)，其中group(x,y)表示y种物品抽x种的组合数。
5. 上诉的概率公式的计算涉及指数运算，可能非常大，必须考虑溢出，需要使用快速幂
6. 计算简化：上诉计算含分母，计算损失精确度，将计算分为分子部分和分母部分的计算，a为分子，b为分母
   a=sum(group(j-1,k-1)2^(i+j-1-k))(i<=k<=i+j-1) b=2^(i+j-1)
7. 由于答案要求a/b是互质的，而b仅含2这个因子，而3<=p<=10000,即p一定不为偶数，由同余的定义知a/b不互质并不影响结果，证明如下：假设a/b约分后为c/d，约去了公约数k，则（c-dx）mod p=0，而（a-bx）mod p=k（c-d*x）mod p=0，结果仍然为x，故无需约分
8. 细节优化，每输入一组计算一个结果保存到result[T]中

代码实现

#include
#include
using namespace std;

int *up;	//存放组合数分子的辅助空间 

//组合数的计算 
long long group(int x,int y,int mod){
     
	long long result=1;
	if(x==y) return 1; 
	if(y-x<x) x=y-x;		//计算对称的较少计算的组合数 
	for(int i=0;i<x;i++)	//组合数中的分子 
		up[i]=y-i;
	bool flag;
	int t,k;
	for(int i=x;i>=2;i--){
     	//除去分母 
		flag=false;
		for(int j=0;j<x;j++){
     
			if(up[j]%i==0){
     
			 	up[j]/=i;
			 	flag=true;
			 	break;
			}
		}
		if(!flag){
     
			//除分母遗漏，补约分 
			t=i,k=2;
			while(t!=1){
     
				if(t%k==0){
     
					for(int j=0;j<x;j++){
     
						if(up[j]%k==0){
     
							up[j]/=k;
							t/=k;
							break;
						}
					}
				}else k++;
			}
		}
	}
	for(int i=0;i<x;i++)
		result=result*(up[i]%mod)%mod;
	return result;
}

//左移计算 
long long lift_move(long long s,int b,int mod){
     
	for(int i=0;i<b;i++)
		s=(s+s)%mod;
	return s;
}

int main(){
     
    int T,x,y,p,k;
    long long a,b,t,bx;
    up=new int[50000000];
    //get_prim(); 
    cin>>T;
    int *result=new int[T]; 
    for(int i=0;i<T;i++){
     
    	cin>>x>>y>>p>>k;
    	a=0,b=0;
    	result[i]=0;
    	for(int j=0;j<k;j++) cin>>t;	//无视小兵血量
		//计算己方英雄击中多少次死亡 
		t=x%10;
		if(t) x=x/10+1;
		else x=x/10;
		//计算敌方英雄击中多少次死亡
		t=y%10;
		if(t) y=y/10+1;
		else y=y/10;
		for(k=y;k<=x+y-1;k++){
     							//a的计算 
			t=group(y-1,k-1,p);							//组合数的计算 
			if(t==0) continue;
			t=lift_move(t,x+y-1-k,p);					//乘以2^(x+y-1-k)可以直接左移x+y-1-k
			a=(a+t)%p;
		} 
		b=lift_move(1,x+y-1,p);							//b的计算
		for(int j=1;j<=p;j++){
     							//结果的计算 
			bx=b*j%p;
			if(a==bx){
     
				result[i]=j;
			}
		}
	}
	for(int i=0;i<T;i++){
     
		cout<<result[i];
		if(i!=T-1) cout<<endl;
	}
	return 0;
}