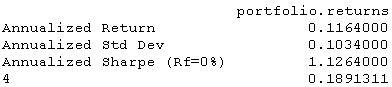R语言改进的股票配对交易策略分析SPY-TLT组合和中国股市投资组合
原文链接:http://tecdat.cn/?p=22034
相信大家都听说过股票和债券的多元化投资组合。改进的股票配对交易策略基本上使用了一种前进的方法(参考文章中的概念),即最大化夏普比率,偏向于波动率而不是收益率。也就是说,它使用72天的移动窗口来最大化投资组合的不同权重配置之间的总收益,标准差提高到52的幂。说得通俗一点,在1的幂数下,这是基本的夏普比率,在0的幂数下,只是一个动量最大化的算法。
这个策略的过程很简单:每个月重新平衡SPY和TLT之间5%的倍数,之前最大化了以下数量(在72天窗口中返回波动率^2.5)。
SPY和TLT组合
以下是获取数据和计算必要数据的代码:
require(quantmod)
getSymbols(c("SPY", "TLT"), from="1990-01-01")
for(i in 1:21)
weightSPY <- (i-1)*.05
config <- Return.portfolio(R = returns, weights=c(weightSPY, weightTLT)
period <- 72
接下来,建立权重的代码:
weights <- t(apply(monthlyModSharpe, 1, findMax))
weights[is.na(weights)] <- 0
也就是说,在每个重新平衡的日期(每月的月末),简单地采用使每月修改的夏普比率计算最大化的设置。接下来是收益表现:
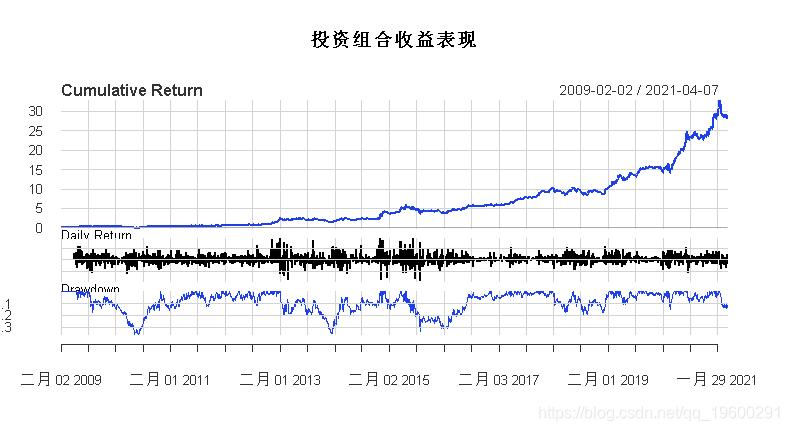
Performance(stratRets)结果如下:
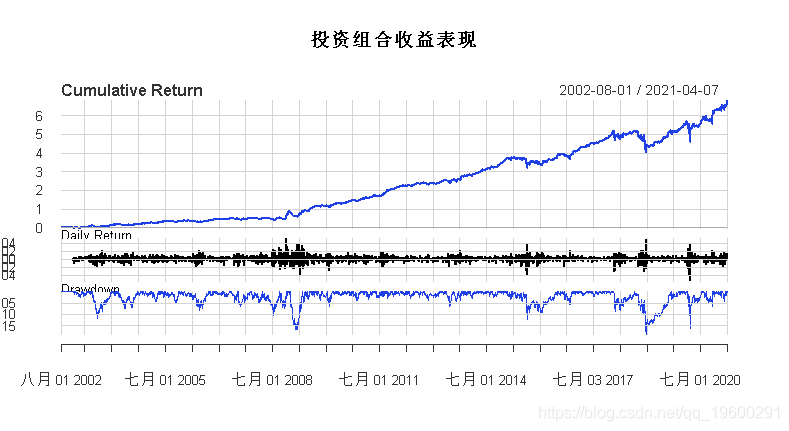
具有以下股票曲线:
并不完美,但相比之下,它的成分如何呢,我们来看看。
apply.yearly(Components, Return.cumulative)以下是一些常见的统计数据:
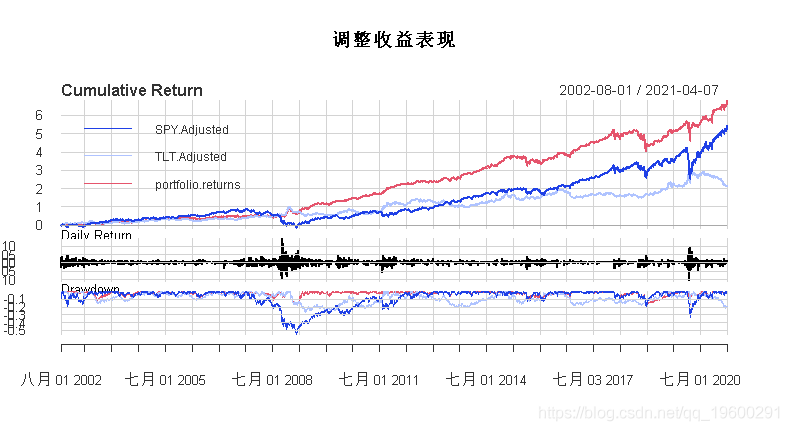
简而言之,这一策略的表现似乎远远好于上述两种成分。我们来看看股票曲线的比较是否反映了这一点。
事实上,虽然它确实在危机中出现了下跌,但当时这两个工具都在下跌,所以看起来这个策略在糟糕的情况下取得了最好的效果.以下是年度收益。
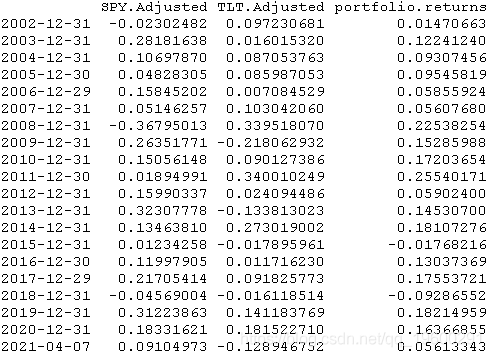
yearly(Return.cumulative)
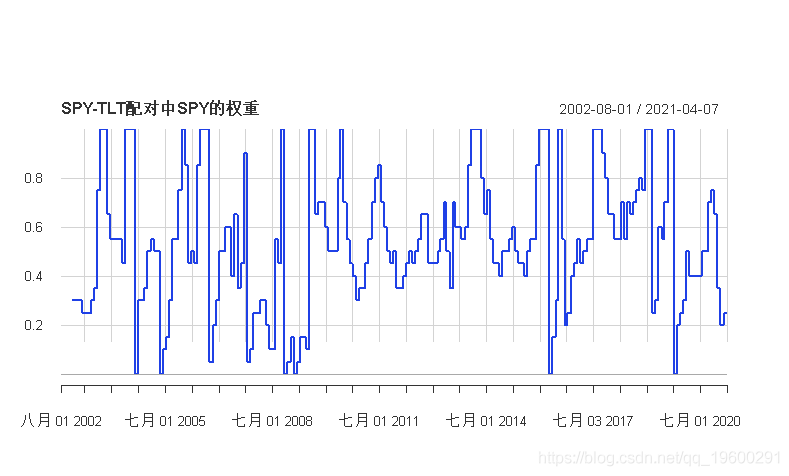
然而,从2002年整体上看,虽然该策略很少会像两个中更好的表现一样,但它总是比两个中更差的表现出色--不仅如此,即使在一个表现差的时候,该策略在回测的每一年中都取得了积极的表现,例如2008年的SPY,以及2009年和2013年的TLT。以下是SPY在策略中的权重。
weightSPY <- do.call(rbind, weightSPY)
TimeSeries(alig, date.format="%Y", ylab="SPY权重", main="SPY-TLT配对中SPY的权重")贵州茅台和民生银行组合
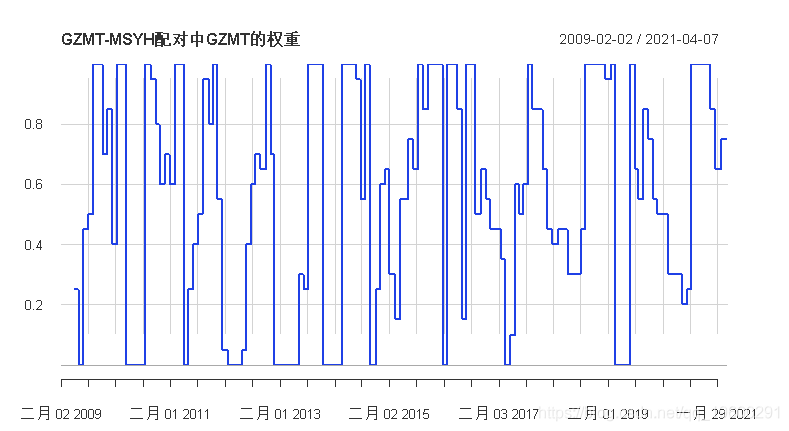
股票数据获取及整理
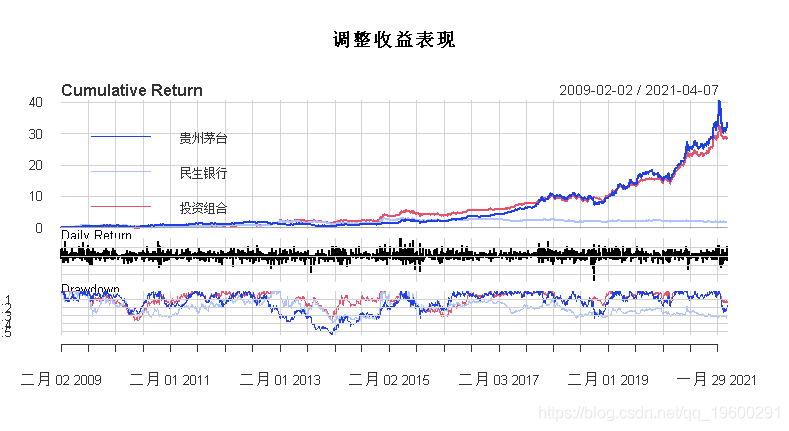
## [1] "GZMT" "MSYH"组合收益表现结果如下:
加入比较项-非组合下的单只表现
年化收益率比较
通过累积收益率、日收益率和最大回撤率,以及年化收益率比较,可以发现采用优化方法的投资组合明显优于传统的投资策略。
现在,虽然这对某些人来说可能是一个独立的策略,但在我看来,动态地重新加权两个具有负相关性的收益流,与它们形成的成分相比,可能会产生一些较好的结果。此外,模拟实际组合收益率所采用的方法很有趣,不是简单地依靠一个数字来总结两种工具之间的关系,毫无疑问,这种方法作为一种一般的前进方法,有着广泛的应用。
最受欢迎的见解
1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用
2.R语言GARCH-DCC模型和DCC(MVT)建模估计
3.R语言实现 Copula 算法建模依赖性案例分析报告
4.R语言COPULAS和金融时间序列数据VaR分析
5.R语言多元COPULA GARCH 模型时间序列预测
6.用R语言实现神经网络预测股票实例
7.r语言预测波动率的实现:ARCH模型与HAR-RV模型
8.R语言如何做马尔科夫转换模型markov switching model
9.matlab使用Copula仿真优化市场风险