广度优先搜索
本节我们要讲解的算法是广度优先搜索(BFS)。顾名思义,广度优先搜索和深度优先搜索的区别在于,深度优先搜索是一条路走到底,再继续寻找下一条路;而广度优先搜索则是试图探寻每一步可能的路径。
按照惯例,我们先来看一道板子题:
-
题目背景
《爱与愁的故事第三弹·shopping》最终章。
-
题目描述
爱与愁大神买完东西后,打算坐车离开中山路。现在爱与愁大神在x1,y1处,车站在x2,y2处。现在给出一个n×n(n<=1000)的地图,0表示马路,1表示店铺(不能从店铺穿过),爱与愁大神只能垂直或水平着在马路上行进。爱与愁大神为了节省时间,他要求最短到达目的地距离(a[i][j]距离为1)。你能帮他解决吗?
-
输入格式
第1行:一个数 n
第2行~第n+1行:整个地图描述(0表示马路,1表示店铺,注意两个数之间没有空格)
第n+2行:四个数 x1,y1,x2,y2
-
输出格式
只有1行:最短到达目的地距离
-
解析
-
队列
在开始编码之前,我们需要理解队列的概念。
由于本教程使用的是Python语言,在此我以Python的列表为例:
我们声明一个列表,ls=[1,2,3,4]
我们假设这个列表只能从前面取东西,后面塞东西,所以我们现在只需要用到两个方法:append和del。
-
-
取:通过索引0获取最前面列表的内容,并通过del删掉;
-
塞:通过append方法添加元素。
队列嘛,排队队吃果果,就像上面这个图片,四个人一个队伍,只能最前面的走,从最后面加入到这个队伍里。
-
思路
思路就很简单啦,对每一个节点,判断它上下左右四个方向都哪个方向可以走,然后加入队列里。
每来到一个新节点,把这个节点拿出队列。
然后进行下一个节点的判断。
最后,如果队列为空,就说明遍历结束。
-
代码
def check(x,y,ans):
global final_ans
if x == end_x-1 and y == end_y-1:
final_ans = min(final_ans,ans)
return False
if x > n-1 or y > n-1 or x < 0 or y < 0:
return False
if map_ls[x][y] == 1:
return False
return True
n = int(input())
map_ls = []
for i in range(0,n):
temp_input = list(input())
tmp_input = list(map(int,temp_input))
map_ls.append(tmp_input)
#地图以列表形式存储
first_x,first_y,end_x,end_y = map(int,input().split())
My_queue = []
My_queue.append([first_x-1,first_y-1,0])
final_ans = 999999
while My_queue:
first_of_queue = My_queue[0]
del My_queue[0]
mark_x = first_of_queue[0]
mark_y = first_of_queue[1]
ans = first_of_queue[2]
map_ls[mark_x][mark_y] = 1
if check(mark_x+1,mark_y,ans):
My_queue.append([mark_x+1,mark_y,ans+1])
if check(mark_x-1,mark_y,ans):
My_queue.append([mark_x-1,mark_y,ans+1])
if check(mark_x,mark_y+1,ans):
My_queue.append([mark_x,mark_y+1,ans+1])
if check(mark_x,mark_y-1,ans):
My_queue.append([mark_x,mark_y-1,ans+1])
print(final_ans+1)
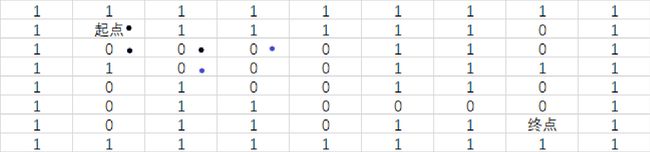
我们把黑色路径设置已经走过的路径,蓝色路径设为现在要走的路径
可以看到,对于图1中的两个蓝色标记,我们分别做了两次判断,并且判断了他们下一次要走的路径
这其实就是为何“广度”优先。
下面是习题时间~
P1443
-
题目描述
有一个n*m的棋盘(1
-
输入格式
一行四个数据,棋盘的大小和马的坐标
-
输出格式
一个n*m的矩阵,代表马到达某个点最少要走几步(左对齐,宽5格,不能到达则输出-1)
-
思路
把方向数组设置为马的八种方向,然后继续广度优先搜索。
每次到一个新的点,如果这个点还是-1,就标记为步数。
最后输出这个列表即可~ -
代码
n,m,f_x,f_y = map(int,input().split())
dir = [[-2,-1],[-2,1],[-1,2],[-1,-2],[1,2],[1,-2],[2,-1],[2,1]]#方向数组,八个方向为马可以走的方向。
ls = []#空列表,用于存储地图
for i in range(0,n):#将ls填充为一个-1构成的m*n的嵌套列表
ls.append([-1]*m)
queue = [[f_x-1,f_y-1,0]]#将起点添加进队列
def judge_bfs(x,y):#此函数作用为判断x,y对应的元素是否应该存入队列
if x > n-1 or x < 0 or y > m-1 or y < 0:
return False
if ls[x][y] != -1:
return False
return True
while queue != []:#循环条件:队列不为空
ls_cp = queue[0]#复制列表首个元素
del queue[0]#出队列
x = ls_cp[0]
y = ls_cp[1]
num_step = ls_cp[2]
ls[x][y] = num_step#标记
for i in range(0,8):
if judge_bfs(x+dir[i][0],y+dir[i][1]):#方向数组遍历
queue.append([x+dir[i][0],y+dir[i][1],num_step+1])
#输出部分
for i in ls:
for j in i:
print(j,end='')
num_space = 5 - len(str(j))#补足五位
print(" " * num_space, end = '')
print("")
P1596
-
题目描述
由于近期的降雨,雨水汇集在农民约翰的田地不同的地方。我们用一个NxM(1<=N<=100;1<=M<=100)网格图表示。每个网格中有水(‘W’) 或是旱地(’.’)。一个网格与其周围的八个网格相连,而一组相连的网格视为一个水坑。约翰想弄清楚他的田地已经形成了多少水坑。给出约翰田地的示意图,确定当中有多少水坑。
-
输入格式
第1行:两个空格隔开的整数:N 和 M 第2行到第N+1行:每行M个字符,每个字符是’W’或’.’,它们表示网格图中的一排。字符之间没有空格。
-
输出格式
一行:水坑的数量
-
思路
BFS求连通块个数。
循环地图内每一个元素,对每一个元素进行一次bfs搜索。
每次bfs搜索时,把所有经过的地图标记为不可走。
最后,循环地图内每一个元素时,bfs次数就是连通块的个数。
-
代码
n,m = map(int,input().split())
ls = []
dir = [[1,1],[-1,1],[1,-1],[-1,-1],[0,1],[0,-1],[1,0],[-1,0]]
for i in range(0,n):
temp_input = list(input())
ls.append(temp_input)
#输入部分结束
def judge_map(x,y):
if x>n-1 or y > m-1 or x < 0 or y < 0:
return False
if ls[x][y] == '.':
return False
return True
#地图判断函数
def bfs(x,y):
global ls
queue = [[x,y]]
while queue != []:
ls_cp = queue[0]
del queue[0]
ls[ls_cp[0]][ls_cp[1]] = '.'
for i in range(0,8):
if judge_map(ls_cp[0]+dir[i][0],ls_cp[1]+dir[i][1]):
queue.append([ls_cp[0]+dir[i][0],ls_cp[1]+dir[i][1]])
#bfs函数核心部分
ans = 0
for i in range(0,n):
for j in range(0,m):
if judge_map(i,j):
ans += 1
bfs(i,j)
#主函数部分结束
print(ans)
#输出部分结束
转载自本人的个人博客,www.fengjx.cn。