Mysql数据库调优——索引

Mysql数据库调优——索引

 

参考资料：

MySQL分区：https://www.bilibili.com/video/BV1E7411q7Nx

MySQL_基础+高级篇- 数据库 -sql -mysql教程_mysql视频_mysql入门_尚硅谷：https://www.bilibili.com/video/BV12b411K7Zu

实体书籍：数据库事务并发处理的艺术 事务管理与并发控制 李海翔 等著

博文中部分图片和文字源自网络。部分文字，因学习时记录的笔记时间已久远，无法找到出处，侵删。

---

不论是面试还是正常工作，sql因为其语言本身的阅读和书写性非常贴近人类语言的语法，所以面试的时候，并没有什么好问的，最多是写写sql多表查询或者子查询这种量级的sql语句，重点基本都集中在一下几个部门了：

ACID都是怎么实现的（其实就是变着花样问MVCC（Mysql使用快照隔离实现）、封锁技术、log（Redo/undo））；

大表优化（索引，分区，分表）

基本是从sql调优和Mysql的InnoDB的底层入手，展开各种各样的概念或者场景问题。

---

本文内容大部分来自于MySQL_基础+高级篇- 数据库 -sql -mysql教程_mysql视频_mysql入门_尚硅谷：https://www.bilibili.com/video/BV12b411K7Zu

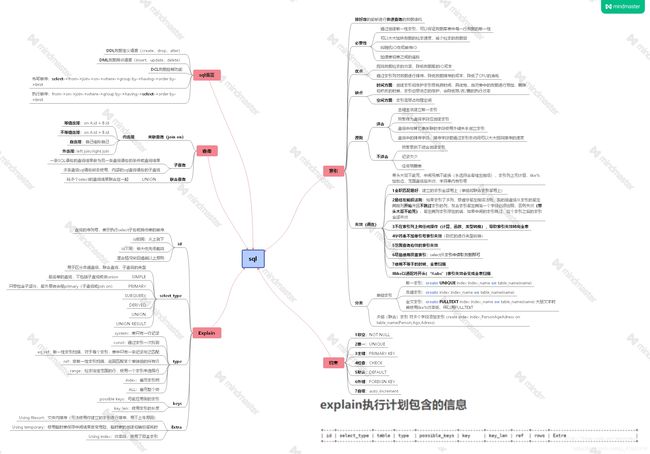
思维导图如下：

目录

Mysql数据库调优——索引

1，诊断缺陷—EXPLAIN

1.1，id

1.2，select type

1.3，key

1.4，type

1.5，extra

2，索引调优

2.1，索引

2.1.1 什么是索引

2.1.2 创建索引的必要性

2.1.3 优缺点

2.1.4 添加索引的原则

2.2，InnoDB底层索引的实现

2.2.1 B树

2.2.2 B+树

2.2.3 二者区别

2.2.4 索引和B+树的关系

2.3，索引调优

---

 

1，诊断缺陷—EXPLAIN

既然要调优，那么首先要知道目前的sql语句存在什么样的缺陷，才可对症下药。

EXPLAIN SELECT ............

在你的select语句前面，增加 explain关键字，运行，即可生成一张信息表

 

在这张表中，有几个比较重要的参数：

1.1，id

查询的序列号，表示执行select子句或操作表的顺序

id相同：从上到下

id不同：谁优先级越高

混合情况依旧遵循以上原则

1.2，select type

用于区分普通查询，联合查询，子查询的类型

SIMPLE：最简单的查询，不包括子查询或者unicon

PRIMARY:

1.3，key

possible key：可能应用到的索引

key_len：索引长度

key：实际中会用到的索引

1.4，type

system：表只有一行记录

const：通过索引一次找到

eq_ref：唯一性索引扫描，对于 每个索引，表中只有一条记录与之匹配

ref：非唯一性索引扫描，返回匹配某个单独值的所有行

range：检索给定范围的行，使用一个索引来选择行

index：遍历索引树

All：遍历整个表

1.5，extra

using filesort：文件内排序（无法使用你建立的索引进行查找或者排序）

using temporary：更危险，因为生成了临时表，临时表的创建和销毁都耗时

using index：效率高，使用了覆盖索引

 

如果sql语句已经优化到了极致，此时效率依旧无法达到要求，那么可以使用分表，提高并发，利用分区，提高磁盘I/O的读写效率

2，索引调优

既然我们已经找到了问题所在，那么就对症下药即可。

按照正确的方式方法增加索引，按照正确的方式书写sql语句，即可完成优化，下面我们来看看这些基本原则都有什么。

2.1，索引

2.1.1 什么是索引

排好序的能够进行快速查询的数据结构

三个要点：排好序，快速查询，数据结构

2.1.2 创建索引的必要性

1. 通过创建主键（默认唯一约束），可以保证数据库表中每一行数据的唯一性
2. 可以大大加快数据的检索速度，减少索引的数据量
3. 将随机I/O变成顺序I/O
4. 加速表和表之间的联系

2.1.3 优缺点

优点

提高数据检索的效率，降低数据的IO成本

通过索引列对数据进行排序，降低数据排序的成本，降低CPU的消耗

缺点

时间方面：创建索引和维护索引要耗费时间，具体地，当对表中的数据进行增加，删除和修改的时候，索引也要动态的维护，会降低增/删/改的执行效率

物理方面：索引需要占物理空间

2.1.4 添加索引的原则

什么情况适合创建索引呢？

1. 频繁作查询的字段应该创建索引
2. 查询中与其他表关联的字段使用外键关系创立索引
3. 查询中的排序字段，排序字段若通过索引去访问可以大大提高排序的速度

什么情况不适合创建索引？

1. 频繁更新不适合创建索引
2. 记录太少
3. 经常增删表

2.2，InnoDB底层索引的实现

底层实现为B+树，要说B+树，先要从B树说起。

2.2.1 B树

文件索引、数据库索引：一般用树形结构进行存储

树形结构例如B树、B+树、二叉查找树都是有序的（每个结点的左子树结点都小于根结点，每个右子树的结点都大于根结点）

查询效率很高，都是O（logN），N为树的高度

Hash表也是很好的一种数据结构，在时间复杂度O(1)下，即可找到要找的元素，唯一的弊端是我们进行模糊查询或者范围查询时，需要遍历所有的数据。

那么我们一般DML语句和DQL语句执行时，都是从磁盘中将数据读取出来后进行处理，磁盘IO和内存的速度根本没有办法比较，在磁盘中读取数据时，是按照页为单位进行读取的，如果每次读取到的数据量大于一个页，那么就会多一次磁盘IO。

现在我们要找一种数据结构在磁盘中保存数据，查询效率高，同时IO操作要少。

如果是二叉查找树的话，因为只有二叉，显然存储大量数据时，树高会很高，那么如此情况下进行查找时，磁盘IO此时会很多，效率很低。

此时我们需要采用多叉搜索树——B Tree存储数据。

因为树结构的查找效率和树的高度有这决定性的关系，树越矮，那么IO次数就一定会小

但是树越矮越好吗？不见得，磁盘读取数据是按照页为单位的，如果树过于的矮，那么每次从一个结点开始去访问其孩子结点时，遍历的访问次数会大于一个页，会增加一次IO操作，显然影响效率。

现在假设多叉查找树为M阶，阶数 表示 此树的结点 最多 有 多少个孩子结点（子树）。

那么M一定是根据页的大小来确定的，在不同的操作系统中，页的大小不一样，linux操作系统中页的大小为4kb。

也就是说，每个结点中的元素个数，和该结点的孩子个数，上限都不能超过M，否则会增加IO操作，降低效率。

在增删结点的过程中，也有可能会出现某些结点的元素或者孩子数量很少，这样也会影响到查询的效率

那么规定，每个结点的元素和孩子结点数不得少于M/2个。

所以B树有以下几个特点，其中大部分都是关于结点中元素个数和结点孩子个数的规定

1. 根结点至少有两个孩子
2. 每个中间结点都包换k-1个元素和k个孩子，其中M/2 <= K <= M
3. 每一个叶子结点都包含k-1个元素，其中M/2 <= K <= M
4. 所有的叶子结点都在同一层
5. 每个结点中的元素从小到大排列，结点中k-1个元素正好是k个孩子包含的元素的值域划分

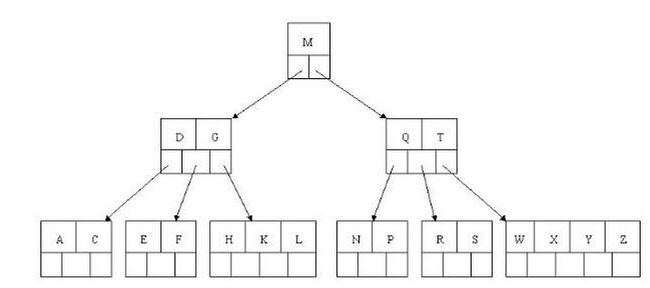
图为3阶B树 

图源：https://zhuanlan.zhihu.com/p/27700617

2.2.2 B+树

B树虽好，但是还有问题

1. 每个结点中既要有索引信息，也要存对应的数据，如果数据很大，树的体积就很大。
2. B树遍历整个树的过程和二叉树本质上是一样的，B树相对二叉树虽然提高了磁盘IO性能，但并没有解决遍历元素效率低下的问题

针对以上两个问题B+树诞生了，B+树相比B树，本质上是一样的，结点中元素和每个结点的孩子结点个数的数量爱要求都是一样。

（修复问题1）

区别在于B+树的所有根结点都不带任何的数据信息，只有索引信息，所有数据信息全部存储在叶子结点里，这样，整个树的每个结点所占的内存空间就变小了，读到内存中的索引信息就会更多一些，相当于减少了磁盘IO次数。

（修复问题2）

因为B+树叶子结点是双向链表，所以可以很方便的进行范围查询

 

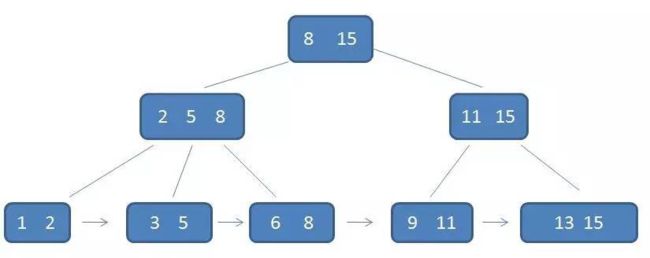
那么就在B树的基础上，进行部分的改进，我们将B树的叶子结点，变成一个双向链表，有利于范围查询

图源：https://www.jianshu.com/p/71700a464e97

2.2.3 二者区别

IO操作：

B树的查找只需找到匹配元素即可，最好情况下查找到根结点，最坏情况下查找到叶子结点，所以性能不稳定

但是B+树每次都是从根结点到叶子结点，性能很稳定。

范围查询：

B树的范围查询需要不断依赖中序遍历。不适合范围查询

B+树因为叶子结点是彼此相连接的双向链表，范围查询极其方便，知道范围长度，上限或者下限即可。

2.2.4 索引和B+树的关系

sql中的索引分类很简单：

单值索引：普通（就没有多余关键字），唯一（unique），全文索引（InnoDB还不支持）

多值索引：在多个字段上创建一个索引

但是写好不犯错可不简单，使用索引中最关键的一个原则：最左前缀原则

其中有很多因最左前缀延伸的原则，后面会详细赘述，这里主要是解释为什么会有最左前缀原则？

主要还是因为InnoDB底层使用B+树作为数据存储结构

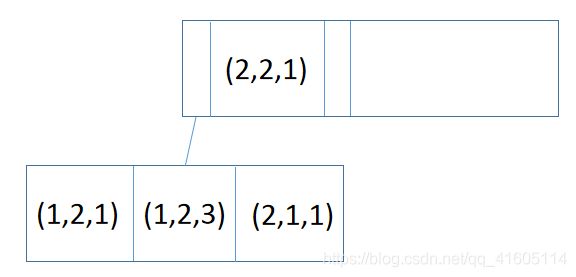
如果创建了一个（a,b,c）这么一个联合索引

可以看到，a的值是有顺序的，而b的值是没有顺序的，c也无需。

如果我们不遵循最左前缀的原则，以b为第一条件进行排序，那么显然是要全表扫描的，无法利用索引。

而范围查询后右侧的索引失效也是一定的，比如 

select * 
from test
where a = 1,b between 10 and 12,c = 3

索引命中a，b，但是无法命中c

 

2.3，索引调优

2.3.1 最左前缀法则

最左前缀法则的种种衍生，范围查询索引失效，全职匹配最优等，都是因为数据库底层使用B+树的结构所导致的。

这部分上面有所赘述

2.3.2 不在索引列上做任何操作（计算，函数，类型转换），这会导致索引失效，搜索转向全表

2.3.3 字符串不加单引号索引失效（发生了隐式的类型转换）

2.3.4 范围查询右侧的索引失效

2.3.5 使用不等于的时候，全表扫描

2.3.6 like以通配符开头（'%abc'）索引失效会变成全表扫描