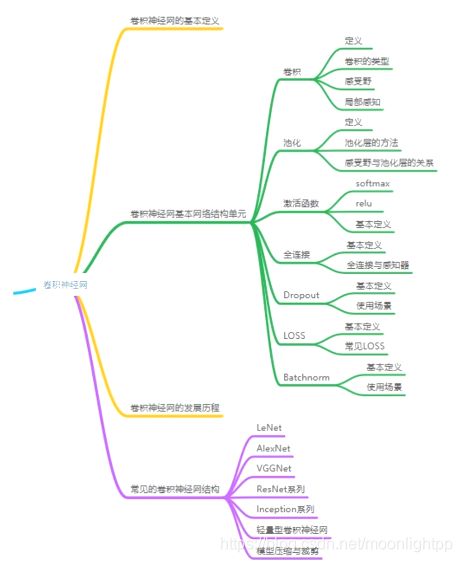
卷积神经网络
卷积神经网络
知识脉络:
什么是卷积神经网:
卷积网络是以卷积结构为主,搭建起来的深度网络
将图片作为网络的输入,自动提取特征,并且对图片的变形(如平移、比例缩放、倾斜)等具有高度不变形
卷积神经网的重要组成单元:
卷积
池化
激活
BN(Batch Normalization)
FC(Fully Connected)
LOSS
其它层
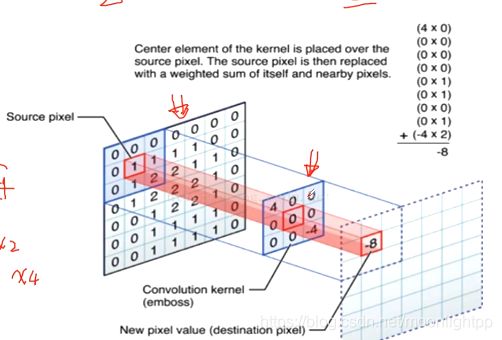
卷积的基本定义:
对图像和滤波矩阵做内积的操作
1.滤波器(边缘提取,图像降噪,图像锐化)
2.每种卷积对应一种特征
3.lm2col实现卷积计算
卷积中的重要参数:
卷积核
1.最常用为2D卷积核(k_w*k_h)
2.权重和偏置项
3.常用卷积核:1*1,3*3,5*5
注:奇数卷积核具有中心点,能够保护位置信息
卷积—权值共享和局部连接
1.卷积运算作用在局部
2.Feature map使用同一个卷积核运算后得到一种特征
3.多种特征采用多个卷积核(channel的数量为输出l)

感受野
1.3*3卷积核对应3*3感受野,卷积核越大,感受野越大
2.5*5卷积核需要对25个值进行乘加运算,计算量较大
3.2个3*3卷积核能够替代1个5*5卷积核
4.3个3*3卷积核能够替代1个7*7卷积核
步长(stride)
Feature Map(Ouput size):(N-F)/stride+1
stride=a =>下采样a倍(移动a格)
卷积的定义和使用(tensorflow):
filter_weight = tf.get_variable('weight', [5, 5, 3, 6]),
initialzer = tf.truncated_normal_initialzer(stddev=0.1)
biases = tf.get_variable('biases', [16], initialzer=tf.constant_initializer(0.1))
conv = tf.nn.conv2d(input, filter_weight, strides=[1, 1, 1, 1], padding='SAME')
bias = tf.nn.bias_add(conv, biases)
池化的基本概念:
池化:对输入的特征图进行压缩
1.使特征图变小,简化网络计算复杂度
2.进行特征压缩,提取主要特征
3.增大感受野(最大值池化)
常见的池化策略
1.最大池化(Max Pooling)
2.平均池化(Average Pooling)
3.随机池化(Stochastic Pooling)
激活函数的基本概念:
增加网络的非线性,进而提升网络的表达能力
1.非线性
2.单调性
3.可微性
4.取值范围
常见的激活函数:Sigmoid,Tanh,ReLU
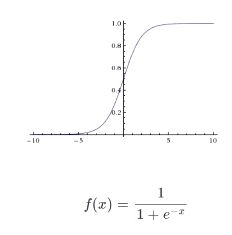
Sigmoid
1.梯度弥散/梯度饱和
2.指数运算
3.输出不是以0为中心
Tanh
1.双曲正切函数
2.完全可微分的,反对称,对称中心在原点
3.指数运算

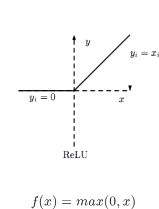
ReLu
1.修正线性单元
2.只有输出超出阈值时神经元才激活(当x>0时神经元被激活)
3.函数形式简单,正数时不存在梯度饱和
4.一旦输入到了负数,ReLU就会死掉
注:通过调整learning rate来保证网络处于激活状态
Batch Normalization层的基本概念:
1.通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回均值为0方差为1的标准正态分布
2.对于原始输入数据,数据分布是不可控的,所以我们要将其规范化
Batch Normalization层的使用(tensorflow):
使用BN层需要注意:
tf.contrib.layers.batch_norm
# 处于渲染状态:True 测试时:false
training = True
# 更新边层参数
tf.get_collection(tf.GraphKeys.UPDATE_OPS)
Fully Connected层:
连接所有的特征,将输出值送给分类器
1.将网络的输出变成一个向量
2.可以采用卷积代替全连接层
3.全连接层是尺度敏感的
4.配合使用dropout层
dropout层:
在训练的过程中,随机的丢弃一部分输入,此时丢弃部分对应的参数不会更新
-缓解过拟合问题
1.取平均的作用
2.减少神经元之间复杂的共适应关系
Loss层:
损失函数:用来评估模型的预测值和真实值的不一致程度
1.经验风险最小
2.结构风险最小
损失层定义了使用的损失函数,通过最小化损失来驱动网络的训练
1.网络的损失通过前向操作计算
2.网络参数相对于损失函数的梯度则通过反向操作计算(分类任务损失:交叉熵损失;回归任务损失:L1损失,L2损失)
交叉熵损失
-满足似然损失的性质
当真实输出a与期望输出y接近的时候,代价函数接近于0