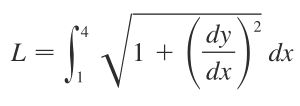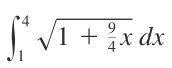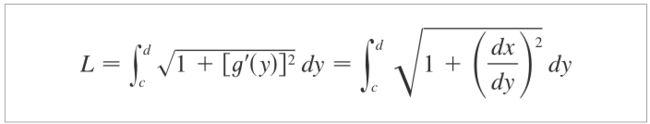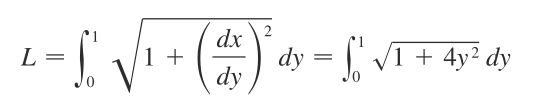探索创新科技: Lite-Mono - 简约高效的小型化Mono框架
杭律沛Meris
探索创新科技:Lite-Mono-简约高效的小型化Mono框架Lite-Mono[CVPR2023]Lite-Mono:ALightweightCNNandTransformerArchitectureforSelf-SupervisedMonocularDepthEstimation项目地址:https://gitcode.com/gh_mirrors/li/Lite-Mono如果你在寻找一个轻
SQL查询技巧:深入解析学生选课系统数据库
天冬忘忧
SQL数据库sqloracle
在大学的学生选课系统中,数据库的管理和查询是日常操作中的重要部分。本文通过一系列具体的SQL查询示例,深入解析如何高效地从数据库中获取所需信息,包括学生选课情况、成绩分析、教师课程管理等。系统数据库结构首先,我们有一个包含以下表的数据库:course-存储课程信息建表CREATETABLE`course`(`CNO`varchar(5)NOTNULL,`CNAME`varchar(10)NOTNU
ArcGis Server安装与使用
kiba518
pythonjavalinux数据库git
ArcGisServer安装下载ArcGisServer双击Setup.exe,然后一直下一步。
educoder实训平台python顺序结构答案_Educoder Python顺序结构习题
weixin_39710660
1.正方形与等腰三角形组成的多边形的面积square_length=4triangle_h=2.6area_square=4*4area_triangle=(2.6*4)/2area_total=area_square+area_triangleprint(area_total)2.平抛小球与抛出点的距离G=9.8v0=5t=2s=v0*th=(G*t**2)/2d=(s**2+h**2)**0.
【LINUX】SHELL贪吃蛇
缘起性本空
java前端服务器
MapHeight=19MapWidth=17SnakeLength=3SnakeX=(234)SnakeY=(555)MoveDirection="Right"Food=(714)Map=(11111111111111111119100000000000000000191000000000000000001910000000000000000019100000000000000000191000
ResNet的半监督和半弱监督模型
Valar_Morghulis
Billion-scalesemi-supervisedlearningforimageclassificationhttps://arxiv.org/pdf/1905.00546.pdfhttps://github.com/facebookresearch/semi-supervised-ImageNet1K-models/权重在timm中也有:https://hub.fastgit.org/r
LeetCode[位运算] - #137 Single Number II
Cwind
javaAlgorithmLeetCode题解位运算
原题链接:#137 Single Number II
要求:
给定一个整型数组,其中除了一个元素之外,每个元素都出现三次。找出这个元素
注意:算法的时间复杂度应为O(n),最好不使用额外的内存空间
难度:中等
分析:
与#136类似,都是考察位运算。不过出现两次的可以使用异或运算的特性 n XOR n = 0, n XOR 0 = n,即某一
《JavaScript语言精粹》笔记
aijuans
JavaScript
0、JavaScript的简单数据类型包括数字、字符创、布尔值(true/false)、null和undefined值,其它值都是对象。
1、JavaScript只有一个数字类型,它在内部被表示为64位的浮点数。没有分离出整数,所以1和1.0的值相同。
2、NaN是一个数值,表示一个不能产生正常结果的运算结果。NaN不等于任何值,包括它本身。可以用函数isNaN(number)检测NaN,但是
你应该更新的Java知识之常用程序库
Kai_Ge
java
在很多人眼中,Java 已经是一门垂垂老矣的语言,但并不妨碍 Java 世界依然在前进。如果你曾离开 Java,云游于其它世界,或是每日只在遗留代码中挣扎,或许是时候抬起头,看看老 Java 中的新东西。
Guava
Guava[gwɑ:və],一句话,只要你做Java项目,就应该用Guava(Github)。
guava 是 Google 出品的一套 Java 核心库,在我看来,它甚至应该
HttpClient
120153216
httpclient
/**
* 可以传对象的请求转发,对象已流形式放入HTTP中
*/
public static Object doPost(Map<String,Object> parmMap,String url)
{
Object object = null;
HttpClient hc = new HttpClient();
String fullURL
Django model字段类型清单
2002wmj
django
Django 通过 models 实现数据库的创建、修改、删除等操作,本文为模型中一般常用的类型的清单,便于查询和使用: AutoField:一个自动递增的整型字段,添加记录时它会自动增长。你通常不需要直接使用这个字段;如果你不指定主键的话,系统会自动添加一个主键字段到你的model。(参阅自动主键字段) BooleanField:布尔字段,管理工具里会自动将其描述为checkbox。 Cha
在SQLSERVER中查找消耗CPU最多的SQL
357029540
SQL Server
返回消耗CPU数目最多的10条语句
SELECT TOP 10
total_worker_time/execution_count AS avg_cpu_cost, plan_handle,
execution_count,
(SELECT SUBSTRING(text, statement_start_of
Myeclipse项目无法部署,Undefined exploded archive location
7454103
eclipseMyEclipse
做个备忘!
错误信息为:
Undefined exploded archive location
原因:
在工程转移过程中,导致工程的配置文件出错;
解决方法:
GMT时间格式转换
adminjun
GMT时间转换
普通的时间转换问题我这里就不再罗嗦了,我想大家应该都会那种低级的转换问题吧,现在我向大家总结一下如何转换GMT时间格式,这种格式的转换方法网上还不是很多,所以有必要总结一下,也算给有需要的朋友一个小小的帮助啦。
1、可以使用
SimpleDateFormat SimpleDateFormat
EEE-三位星期
d-天
MMM-月
yyyy-四位年
Oracle数据库新装连接串问题
aijuans
oracle数据库
割接新装了数据库,客户端登陆无问题,apache/cgi-bin程序有问题,sqlnet.log日志如下:
Fatal NI connect error 12170.
VERSION INFORMATION: TNS for Linux: Version 10.2.0.4.0 - Product
回顾java数组复制
ayaoxinchao
java数组
在写这篇文章之前,也看了一些别人写的,基本上都是大同小异。文章是对java数组复制基础知识的回顾,算是作为学习笔记,供以后自己翻阅。首先,简单想一下这个问题:为什么要复制数组?我的个人理解:在我们在利用一个数组时,在每一次使用,我们都希望它的值是初始值。这时我们就要对数组进行复制,以达到原始数组值的安全性。java数组复制大致分为3种方式:①for循环方式 ②clone方式 ③arrayCopy方
java web会话监听并使用spring注入
bewithme
Java Web
在java web应用中,当你想在建立会话或移除会话时,让系统做某些事情,比如说,统计在线用户,每当有用户登录时,或退出时,那么可以用下面这个监听器来监听。
import java.util.ArrayList;
import java.ut
NoSQL数据库之Redis数据库管理(Redis的常用命令及高级应用)
bijian1013
redis数据库NoSQL
一 .Redis常用命令
Redis提供了丰富的命令对数据库和各种数据库类型进行操作,这些命令可以在Linux终端使用。
a.键值相关命令
b.服务器相关命令
1.键值相关命令
&
java枚举序列化问题
bingyingao
java枚举序列化
对象在网络中传输离不开序列化和反序列化。而如果序列化的对象中有枚举值就要特别注意一些发布兼容问题:
1.加一个枚举值
新机器代码读分布式缓存中老对象,没有问题,不会抛异常。
老机器代码读分布式缓存中新对像,反序列化会中断,所以在所有机器发布完成之前要避免出现新对象,或者提前让老机器拥有新增枚举的jar。
2.删一个枚举值
新机器代码读分布式缓存中老对象,反序列
【Spark七十八】Spark Kyro序列化
bit1129
spark
当使用SparkContext的saveAsObjectFile方法将对象序列化到文件,以及通过objectFile方法将对象从文件反序列出来的时候,Spark默认使用Java的序列化以及反序列化机制,通常情况下,这种序列化机制是很低效的,Spark支持使用Kyro作为对象的序列化和反序列化机制,序列化的速度比java更快,但是使用Kyro时要注意,Kyro目前还是有些bug。
Spark
Hybridizing OO and Functional Design
bookjovi
erlanghaskell
推荐博文:
Tell Above, and Ask Below - Hybridizing OO and Functional Design
文章中把OO和FP讲的深入透彻,里面把smalltalk和haskell作为典型的两种编程范式代表语言,此点本人极为同意,smalltalk可以说是最能体现OO设计的面向对象语言,smalltalk的作者Alan kay也是OO的最早先驱,
Java-Collections Framework学习与总结-HashMap
BrokenDreams
Collections
开发中常常会用到这样一种数据结构,根据一个关键字,找到所需的信息。这个过程有点像查字典,拿到一个key,去字典表中查找对应的value。Java1.0版本提供了这样的类java.util.Dictionary(抽象类),基本上支持字典表的操作。后来引入了Map接口,更好的描述的这种数据结构。
&nb
读《研磨设计模式》-代码笔记-职责链模式-Chain Of Responsibility
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/**
* 业务逻辑:项目经理只能处理500以下的费用申请,部门经理是1000,总经理不设限。简单起见,只同意“Tom”的申请
* bylijinnan
*/
abstract class Handler {
/*
Android中启动外部程序
cherishLC
android
1、启动外部程序
引用自:
http://blog.csdn.net/linxcool/article/details/7692374
//方法一
Intent intent=new Intent();
//包名 包名+类名(全路径)
intent.setClassName("com.linxcool", "com.linxcool.PlaneActi
summary_keep_rate
coollyj
SUM
BEGIN
/*DECLARE minDate varchar(20) ;
DECLARE maxDate varchar(20) ;*/
DECLARE stkDate varchar(20) ;
DECLARE done int default -1;
/* 游标中 注册服务器地址 */
DE
hadoop hdfs 添加数据目录出错
daizj
hadoophdfs扩容
由于原来配置的hadoop data目录快要用满了,故准备修改配置文件增加数据目录,以便扩容,但由于疏忽,把core-site.xml, hdfs-site.xml配置文件dfs.datanode.data.dir 配置项增加了配置目录,但未创建实际目录,重启datanode服务时,报如下错误:
2014-11-18 08:51:39,128 WARN org.apache.hadoop.h
grep 目录级联查找
dongwei_6688
grep
在Mac或者Linux下使用grep进行文件内容查找时,如果给定的目标搜索路径是当前目录,那么它默认只搜索当前目录下的文件,而不会搜索其下面子目录中的文件内容,如果想级联搜索下级目录,需要使用一个“-r”参数:
grep -n -r "GET" .
上面的命令将会找出当前目录“.”及当前目录中所有下级目录
yii 修改模块使用的布局文件
dcj3sjt126com
yiilayouts
方法一:yii模块默认使用系统当前的主题布局文件,如果在主配置文件中配置了主题比如: 'theme'=>'mythm', 那么yii的模块就使用 protected/themes/mythm/views/layouts 下的布局文件; 如果未配置主题,那么 yii的模块就使用 protected/views/layouts 下的布局文件, 总之默认不是使用自身目录 pr
设计模式之单例模式
come_for_dream
设计模式单例模式懒汉式饿汉式双重检验锁失败无序写入
今天该来的面试还没来,这个店估计不会来电话了,安静下来写写博客也不错,没事翻了翻小易哥的博客甚至与大牛们之间的差距,基础知识不扎实建起来的楼再高也只能是危楼罢了,陈下心回归基础把以前学过的东西总结一下。
*********************************
8、数组
豆豆咖啡
二维数组数组一维数组
一、概念
数组是同一种类型数据的集合。其实数组就是一个容器。
二、好处
可以自动给数组中的元素从0开始编号,方便操作这些元素
三、格式
//一维数组
1,元素类型[] 变量名 = new 元素类型[元素的个数]
int[] arr =
Decode Ways
hcx2013
decode
A message containing letters from A-Z is being encoded to numbers using the following mapping:
'A' -> 1
'B' -> 2
...
'Z' -> 26
Given an encoded message containing digits, det
Spring4.1新特性——异步调度和事件机制的异常处理
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
squid3(高命中率)缓存服务器配置
liyonghui160com
系统:centos 5.x
需要的软件:squid-3.0.STABLE25.tar.gz
1.下载squid
wget http://www.squid-cache.org/Versions/v3/3.0/squid-3.0.STABLE25.tar.gz
tar zxf squid-3.0.STABLE25.tar.gz &&
避免Java应用中NullPointerException的技巧和最佳实践
pda158
java
1) 从已知的String对象中调用equals()和equalsIgnoreCase()方法,而非未知对象。 总是从已知的非空String对象中调用equals()方法。因为equals()方法是对称的,调用a.equals(b)和调用b.equals(a)是完全相同的,这也是为什么程序员对于对象a和b这么不上心。如果调用者是空指针,这种调用可能导致一个空指针异常
Object unk
如何在Swift语言中创建http请求
shoothao
httpswift
概述:本文通过实例从同步和异步两种方式上回答了”如何在Swift语言中创建http请求“的问题。
如果你对Objective-C比较了解的话,对于如何创建http请求你一定驾轻就熟了,而新语言Swift与其相比只有语法上的区别。但是,对才接触到这个崭新平台的初学者来说,他们仍然想知道“如何在Swift语言中创建http请求?”。
在这里,我将作出一些建议来回答上述问题。常见的
Spring事务的传播方式
uule
spring事务
传播方式:
新建事务
required
required_new - 挂起当前
非事务方式运行
supports
&nbs