R语言test函数均值和方差的检验

单个正态总体均值的检验

library(BSDA)
a <- c(8.05,8.15,8.2,8.1,8.25)
z.test(x=a,mu=8,sigma.x=0.2,alternative="two.sided")

	One-sample z-Test

data:  a
z = 1.6771, p-value = 0.09353
alternative hypothesis: true mean is not equal to 8
95 percent confidence interval:
 7.974695 8.325305
sample estimates:
mean of x 
     8.15 

均值已知，方差未知的单样本t检验

$$\begin{gathered} \sigma 未知时的t检验 \\ t=\frac{x-\mu }{S/\sqrt{n}} \end{gathered}$$

	One Sample t-test

data:  k
t = -2.7951, df = 4, p-value = 0.04906
alternative hypothesis: true mean is not equal to 240
95 percent confidence interval:
 239.0033 239.9967
sample estimates:
mean of x 
    239.5 

k<-c(239.7,239.6,239,240,239.2)
t.test(k,alternative = "two.sided",mu = 240)

双样本的t检验

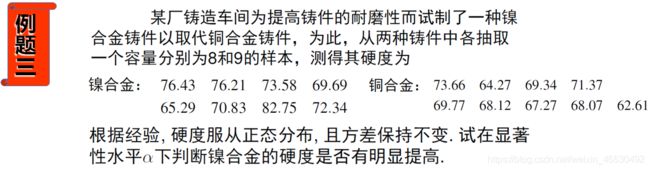
x<-c(76.43,76.21,73.58,69.69,65.29,70.83,82.75,72.34)
y<-c(73.66,64.27,69.34,71.37,69.77,68.12,67.27,68.07,62.61)
t.test(x,y,alternative = "greater",var.equal = T)

	Two Sample t-test

data:  x and y
t = 2.4234, df = 15, p-value = 0.01424
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 1.41478     Inf
sample estimates:
mean of x mean of y 
 73.39000  68.27556 

正态总体方差的检验

x<-c(16.2,16.4,15.8,15.5,16.7,15.6,15.8)
y<-c(15.9,16.0,16.4,16.1,16.5,15.8,15.7,15.0)
var.test(x,y)

	F test to compare two variances

data:  x and y
F = 0.90869, num df = 6, denom df = 7,
p-value = 0.9232
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.1775273 5.1754220
sample estimates:
ratio of variances 
         0.9086909 

二项分布的假设检验

binom.test(7,20,p = 0.4)

	Exact binomial test

data:  7 and 20
number of successes = 7, number of trials
= 20, p-value = 0.8203
alternative hypothesis: true probability of success is not equal to 0.4
95 percent confidence interval:
 0.1539092 0.5921885
sample estimates:
probability of success 
                  0.35