Boosting的思路与Adaboost算法

一、Boosting方法的基本思路

Boosting方法是使用同一组数据集进行反复学习，得到一系列简单模型，然后组合这些模型构成一个预测性能十分强大的机器学习模型，Boosting的特点：

• boosting的目的是减小bias；
• 对权重进行训练；
• 弱组强

Bootsing意为“增强、提升”，首先引入概念：

在概率近似正确学习的框架中，
弱可学习（weakly learnable）：存在一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么就称这个概念是弱科学系的；
强可学习（strongly learnalbe）：存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的；

Robert E. Schapire证明强可学习与弱可学习是等价的，也就是说，在概率近似正确学习的框架下，一个概念是强可学习与弱可学习互为充分必要条件。

关于如何由“弱”变“强”，有很多算法被陆续提出，对于提升算法来说，有两个问题需要回答：

1. 每一轮如何改变训练数据的权值或概率分布；
2. 如何将弱分类器组合成一个强分类器；

接下来我们介绍Boosting提升算法中最具代表性的AdaBoost（adaptive boosting）算法，也被成为自适应增强算法。

二、AdaBoost算法

AdaBoost算法的总体思想：

1. 提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值；
2. 加大分类误差率小的弱分类器的权值，减小分类误差率大的弱分类器的权值；

算法内容如下：

1.输入

训练数据集$T=\left\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\right\}$，$x_i\in \chi \subseteq R^n$,$y_i=\left\{-1,+1\right\}$；

2.输出

最终分类器$G(x)$

3.训练过程

1）初始化训练数据的权值分布

$$D_1=(w_{11},\dots ,w_{1i},\dots ,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,\dots ,N$$

2）计算当前分类器在训练数据集上的分类误差率

$$e_m=P(G_m(x_i)\ne y_i)=\sum _{i=1}^N{w}_{mi}I(G_m(x_i)\ne y_i)$$

3）计算当前分类器的系数并且更新训练数据集的权值分布

$${\alpha }_m=\frac{1}{2}\log \frac{1-e_m}{e_m}$$

$$D_{m+1}=(w_{m+1,1},\dots ,w_{m+1,i},\dots ,w_{m+1,N})$$

$$w_{m+1,i}=\frac{w_{mi}}{Z_m}\exp (-{\alpha }_m{y}_i{G}_m(x_i))$$

$Z_m$是规范化因子，表达式为：

$$Z_m=\sum _{i=1}^N{w}_{mi}\exp (-{\alpha }_m{y}_i{G}_m(x_i))$$

4）得到最终分类器

$$G(x)=sign(f(x))=sign\left[\sum _{m=1}^M{\alpha }_m{G}_m(x)\right]$$

4.部分证明

1）误差最小化等价于规划范因子最小化

2）系数$\alpha$的算式由来

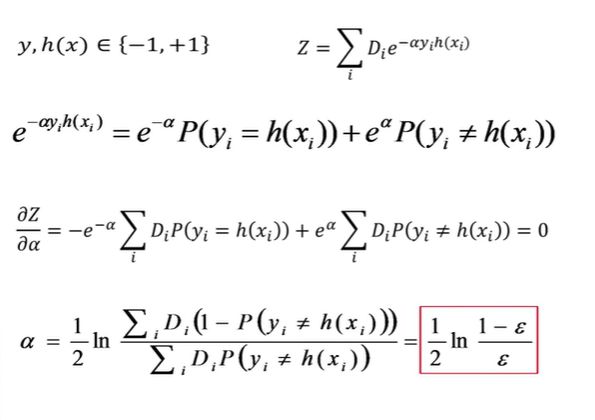
这里有一个小技巧，就是$y_{i}h(x_i)$可以分情况讨论，无需展开。

3）训练次数增多，误差趋于减少

5.举例说明

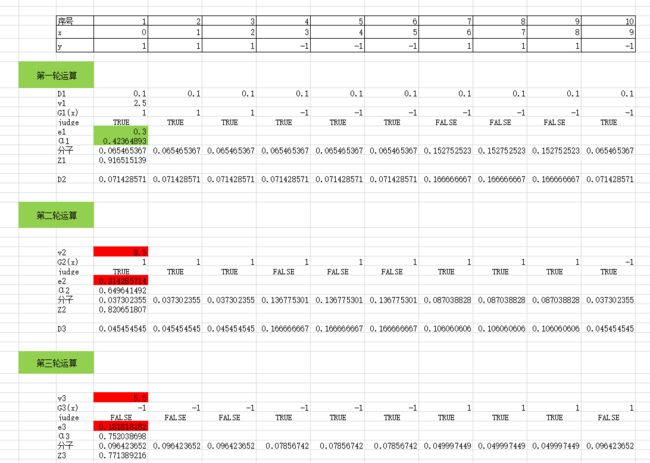
这里的标红的地方是此处用Excel功能不太熟悉，但是可以完全通过条件判断进行自动化求解。

参考文献

[1].清华大学【数据挖掘：集成学习】

[2].Adaboost算法原理分析和实例+代码（简明易懂）

[3].DataWhale组队学习-集成学习（中）