深度学习笔记(1) 线性回归
文章目录
- 一、线性回归的介绍
- 二、解决方法
-
- 1.解析法
- 2.梯度下降法
一、线性回归的介绍
回归分析研究自变量和因变量之间的一种统计关系,在深度学习中通常指给定一个输入,得到一个数作为输出,输入可以是多种形态,比如图像、序列等,如下图所示:

线性回归指输入和输出之间满足线性关系,假设输入数据为 x x x,它有 d d d个特征,输入可以表示为 ( x 1 , x 2 , . . . , x d ) T (x_1,x_2,...,x_d)^T (x1,x2,...,xd)T,那么输出为:
y ^ = w 1 x 1 + w 2 x 2 + ⋅ ⋅ ⋅ + w d x d + b = ∑ i = 1 d w i x i + b \hat y=w_1x_1+w_2x_2+···+w_dx_d+b=\sum_{i=1}^{d} w_ix_i+b y^=w1x1+w2x2+⋅⋅⋅+wdxd+b=i=1∑dwixi+b
将权重记为 ( w 1 , w 2 , ⋅ ⋅ ⋅ , w d ) T (w_1,w_2,···,w_d)^T (w1,w2,⋅⋅⋅,wd)T,我们可以向量化表示上式为: y ^ = w T ⋅ x + b \hat y=w^T·x+b y^=wT⋅x+b
现在有 n n n个样本 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋅ ⋅ ⋅ , ( x n , y n ) (x^1,y^1),(x^2,y^2),···,(x^n,y^n) (x1,y1),(x2,y2),⋅⋅⋅,(xn,yn)(注:本文用上标表示样本标号,用下标表示特征标号),根据上式我们可以计算出这 n n n个样本的预测值:
y ^ 1 = ∑ i = 1 d w i T ⋅ x i 1 + b = w T ⋅ x 1 + b \hat y^1=\sum_{i=1}^{d} w_i^T·x_i^1+b=w^T·x^1+b y^1=i=1∑dwiT⋅xi1+b=wT⋅x1+b
y ^ 2 = ∑ i = 1 d w i T ⋅ x i 2 + b = w T ⋅ x 2 + b \hat y^2=\sum_{i=1}^{d} w_i^T·x_i^2+b=w^T·x^2+b y^2=i=1∑dwiT⋅xi2+b=wT⋅x2+b
⋅ ⋅ ⋅ ··· ⋅⋅⋅
y ^ n = ∑ i = 1 d w i T ⋅ x i n + b = w T ⋅ x n + b \hat y^n=\sum_{i=1}^{d} w_i^T·x_i^n+b=w^T·x^n+b y^n=i=1∑dwiT⋅xin+b=wT⋅xn+b
下面我们要做的就是找到一组参数 w w w和 b b b,使得预测值 y ^ \hat y y^与真实值 y y y之间的差距最小。通常使用均方误差衡量 y y y与 y ^ \hat y y^之间的差异:
L ( w , b ) = ∑ j = 1 n ( y j − y ^ j ) 2 = ∑ j = 1 n ( y j − ( w T ⋅ x j + b ) ) 2 L(w,b)=\sum_{j=1}^{n}(y^j-\hat y^j)^2=\sum_{j=1}^{n}(y^j-(w^T·x^j+b))^2 L(w,b)=j=1∑n(yj−y^j)2=j=1∑n(yj−(wT⋅xj+b))2
L ( w , b ) L(w,b) L(w,b)是一个凸函数,它的值越小,表示预测值和真实值越接近。
我们的目标是: w ∗ , b ∗ = a r g m i n w , b L ( w , b ) w^*,b^*=arg \mathop{min}\limits_{w,b}L(w,b) w∗,b∗=argw,bminL(w,b)。
将 b b b看作 w 0 w_0 w0,加入 x 0 = 1 x_0=1 x0=1,上面的式子就能简化为:
y ^ j = ∑ i = 0 d w i ⋅ x i j = w T ⋅ x j \hat y^j=\sum_{i=0}^{d} w_i·x_i^j=w^T·x^j y^j=i=0∑dwi⋅xij=wT⋅xj
L ( w ) = ∑ j = 1 n ( y j − y ^ j ) 2 = ∑ j = 1 n ( y j − w T ⋅ x j ) 2 L(w)=\sum_{j=1}^{n}(y^j-\hat y^j)^2=\sum_{j=1}^{n}(y^j-w^T·x^j)^2 L(w)=j=1∑n(yj−y^j)2=j=1∑n(yj−wT⋅xj)2
优化目标变为 w ∗ = a r g m i n w L ( w ) w^*=arg \mathop{min}\limits_{w}L(w) w∗=argwminL(w)
二、解决方法
1.解析法
我们可以用解析法得到目标函数的最小值,直接令 d L ( w ) d w = 0 \frac{dL(w)}{dw}=0 dwdL(w)=0,解出 w w w即为最优解。不过解析法计算复杂度大,难以实现,通常不采用。
2.梯度下降法
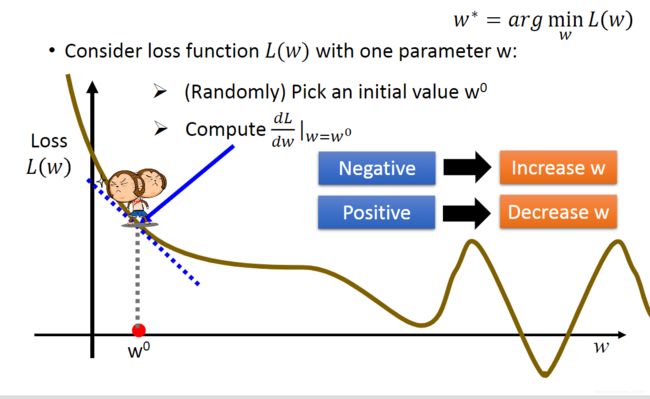
梯度下降法是深度学习中常用的求解方法,首先随机初始化一个参数 w 0 w^0 w0,我们求出 w 0 w^0 w0处的梯度值 d L d w ∣ w = w 0 \frac{dL}{dw}|_{w=w^0} dwdL∣w=w0,如果梯度为正,则减小 w w w;如果梯度为负,则增大 w w w。这里我们需要设置一个超参数叫学习率来控制每次迭代参数的更新量,学习率用 η \eta η表示,那么经过一次迭代后参数更新公式为:
w 1 = w 0 − η d L d w ∣ w = w 0 w^1=w^0- \eta \frac{dL}{dw}|_{w=w^0} w1=w0−ηdwdL∣w=w0
这里的 d L d w \frac{dL}{dw} dwdL是指对 w w w中的每一个分量求导,然后分别更新,即:
( w 1 , w 2 , ⋅ ⋅ ⋅ , w d ) T = ( w 1 , w 2 , ⋅ ⋅ ⋅ , w d ) T − η ( d L d w 1 , d L d w 1 , ⋅ ⋅ ⋅ , d L d w d ) T (w_1,w_2,···,w_d)^T=(w_1,w_2,···,w_d)^T-\eta ( \frac{dL}{dw_1},\frac{dL}{dw_1},···,\frac{dL}{dw_d})^T (w1,w2,⋅⋅⋅,wd)T=(w1,w2,⋅⋅⋅,wd)T−η(dw1dL,dw1dL,⋅⋅⋅,dwddL)T
用同样的过程可以进行下一次迭代,第 k + 1 k+1 k+1次迭代为: w k + 1 = w k − η d L d w ∣ w = w k w^{k+1}=w^k- \eta \frac{dL}{dw}|_{w=w^k} wk+1=wk−ηdwdL∣w=wk ,每次迭代都向梯度的负方向更新参数,使得 L ( w ) L(w) L(w)变得更小。
在经过有限次迭代后,我们可以得到局部极小值,不一定得到全局最小值。如下图所示,当学习率 η \eta η较小时,参数会在 w T w^T wT附近波动,不能到达全局最小值。说明参数的初始化和学习率的设置对结果影响较大。
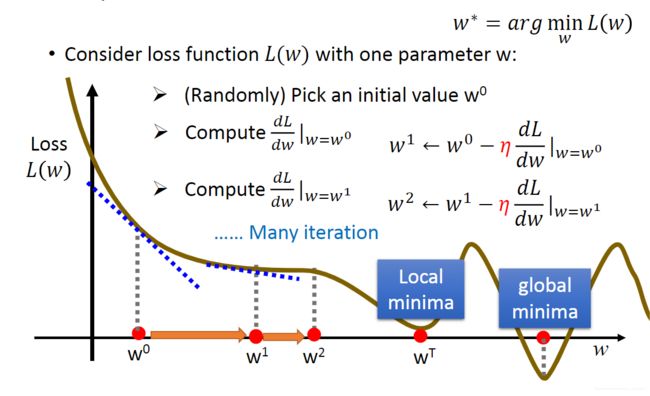
当学习率一定时,在梯度大的地方下降速度快,在梯度小的地方下降速度慢,在鞍点和局部极小值点梯度为0。
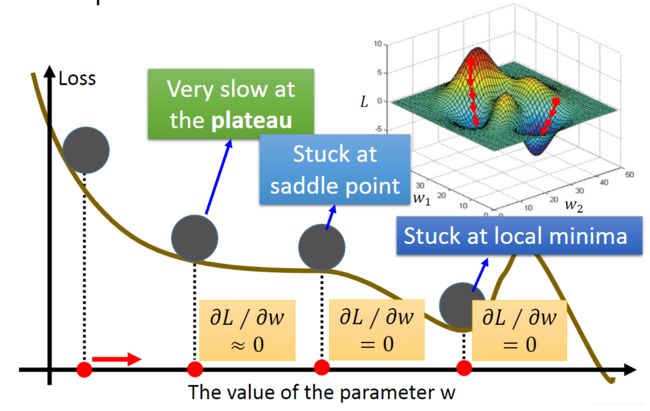
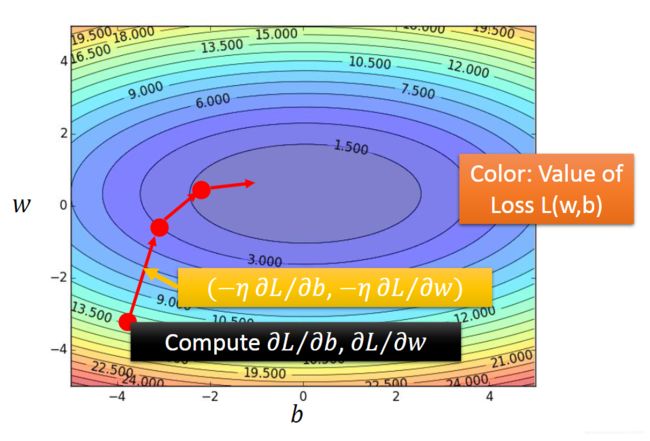
对于线性回归问题情况比较特殊,其损失函数是凸函数,如下图所示,因此无论初始化在哪个位置,经过有限次迭代都能得到全局最优解。我们可以求出梯度,然后迭代求解:
d L ( w ) d w = − 2 ⋅ ∑ j = 1 n ( y j − ( w T ⋅ x j ) ) ⋅ x j \frac{dL(w)}{dw}=-2·\sum_{j=1}^{n}(y^j-(w^T·x^j))·x^j dwdL(w)=−2⋅j=1∑n(yj−(wT⋅xj))⋅xj
本文根据李宏毅老师2020机器学习资料整理。
地址:http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML20.html