python机器学习小记——基于逻辑回归模型的多分类场景预测实战

【阿里天池云-龙珠计划】python机器学习小记

一、逻辑回归算法原理及应用介绍

二、入门Demo

三、基于鸢尾花（iris）数据集的逻辑回归分类实践

---

【写在前面】
接触机器学习也有一年多了，基本都是自学的野路子
借这个天池云龙珠计划的机会好好整理下各种常用算法模型思路以备忘，也给读者抛砖引玉
感谢群主提供的学习机会@AI蜗牛车，群KOL@老表
顺便推荐一下群众的公众号：AI蜗牛车，对上手机器学习很有帮助
那么我们开始吧~~

---

1. 逻辑回归算法原理及应用介绍

1.1. 逻辑回归的介绍

逻辑回归（Logistic regression，简称LR）是一个分类模型，并且广泛应用于各个领域之中。

其最为突出的两点就是其模型简单（部署快！）和模型的可解释性强（用于学术研究的因子分析 & 企业内数分的归因）。

优劣势:

• 优点：实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低；
• 缺点：容易欠拟合，分类精度可能不高

1.2. 逻辑回归的算法原理

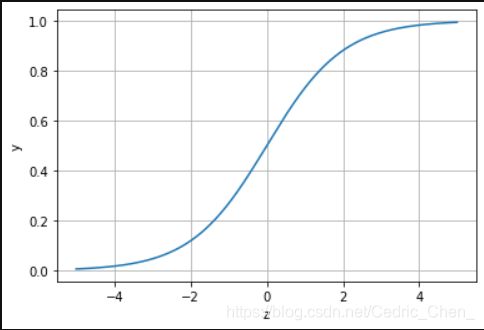
逻辑回归主要用于两分类问题（也可用于多分类，准确性有损失），所以利用了Logistic函数（或称为Sigmoid函数，也常见于神经网络的激活函数），函数形式为：
$$logi(z)=\frac{1}{1+e^{-z}}$$

其对应的函数图像可以表示如下:

import matplotlib.pyplot as plt
x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))

plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()

通过上图我们可以发现 Logistic 函数是单调递增函数，并且在z=0的时候取值为0.5，并且$logi(\cdot )$函数的取值范围为$(0,1)$。

而回归的基本方程为$z=w_0+{\sum }_i^N{w}_i{x}_i$，

将回归方程写入其中为：
$$p=p(y=1|x,\theta )=h_{\theta }(x,\theta )=\frac{1}{1+e^{-(w_0+{\sum }_i^N{w}_i{x}_i)}}$$

所以, $p(y=1|x,\theta )=h_{\theta }(x,\theta )$，$p(y=0|x,\theta )=1-h_{\theta }(x,\theta )$

逻辑回归从其原理上来说，逻辑回归其实是实现了一个决策边界：对于函数 $y=\frac{1}{1+e^{-z}}$,当 $z=>0$时,$y=>0.5$,分类为1，当 $z<0$时,$y<0.5$,分类为0，其对应的$y$值我们可以视为类别1的概率预测值.

对于模型的训练而言：实质上来说就是利用数据求解出对应的模型的特定的$w$。从而得到一个针对于当前数据的特征逻辑回归模型。

而对于多分类而言，将多个二分类的逻辑回归组合，即可实现多分类。

1.3. 逻辑回归的应用

逻辑回归模型广泛用于各个领域，包括机器学习，大多数医学领域和社会科学。在经济学中它可以用来预测一个人选择进入劳动力市场的可能性，而商业应用则可以用来预测房主拖欠抵押贷款的可能性。自然语言处理领域也可有用于文本分类等场景（添加条件随机字段）。

逻辑回归模型现在同样是很多分类算法的基础组件,比如 分类任务中基于GBDT算法+LR逻辑回归实现的信用卡交易反欺诈，CTR(点击通过率)预估等，其好处在于输出值自然地落在0到1之间，并且有概率意义。模型清晰，有对应的概率学理论基础。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。但同时由于其本质上是一个线性的分类器，所以不能应对较为复杂的数据情况。很多时候我们也会拿逻辑回归模型去做一些任务尝试的基线（基础水平）。

2. 入门Demo

## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])  # 2个特征字段（自变量）
y_label = np.array([0, 0, 0, 1, 1, 1])  # 目标字段（因变量）

## 调用逻辑回归模型（from sklearn.linear_model import LogisticRegression）
lr_clf = LogisticRegression()

## 用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2

2.1. 模型参数查看

## 查看对应模型的自变量系数w（0.73，0.69）
print('the weight of Logistic Regression:',lr_clf.coef_)

## 查看其对应模型的常数项系数w0（-0.036）
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)

2.2. 模型可视化

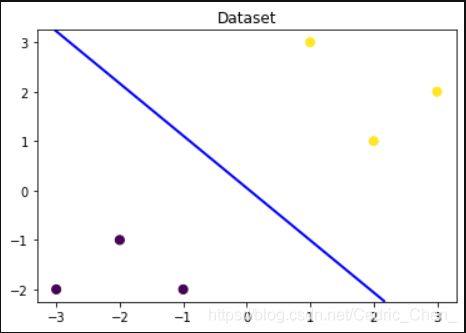
## 可视化构造的数据样本点
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')  # 参数详解：x坐标,y坐标,颜色选择,点size大小，画布选择
plt.title('Dataset')  # 画布标题
plt.show()

可以看见不同目标变量（因变量）已经用颜色加以区分，而两个特征值（自变量）已经映射到了二维坐标平面

下一步，添加逻辑回归的决策边界

nx, ny = 200, 100
x_min, x_max = plt.xlim()  # x边界
y_min, y_max = plt.ylim()  # y边界
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))

z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()])
z_proba = z_proba[:, 1].reshape(x_grid.shape)
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')  # 参考线设置

plt.show()

方便观测多了~~

那么怎么呈现新增样本点呢？

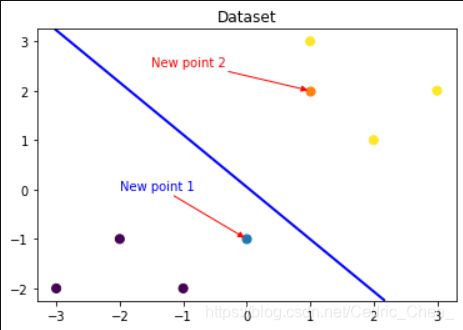
### 可视化预测新样本

plt.figure()
## new point 1 并添加指示箭头
x_fearures_new1 = np.array([[0, -1]])
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 1',xy=(0,-1),xytext=(-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))

## new point 2 并添加指示箭头
x_fearures_new2 = np.array([[1, 2]])
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 2',xy=(1,2),xytext=(-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))

## 训练样本
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')

# 可视化决策边界
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')

plt.show()

2.3. 模型预测

## 在训练集和测试集上分布利用训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1)   # 对new point 1预测
y_label_new2_predict = lr_clf.predict(x_fearures_new2)   # 对new point 2预测

# 预测分类结果
print('The New point 1 predict class:\n',y_label_new1_predict)  
print('The New point 2 predict class:\n',y_label_new2_predict)

## 由于逻辑回归模型是概率预测模型（软分类）,所以我们可以利用 predict_proba 函数预测其概率
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)

# 预测概率结果
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)  # （0.675，0.325）
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)  # （0.110，0.890）

逻辑回归的分类判别是依据概率0.5的决策边界（上图蓝线）

因此可以发现训练好的回归模型将X_new1预测为了类别0（判别面左下侧），X_new2预测为了类别1（判别面右上侧）。

3. 基于鸢尾花（iris）数据集的逻辑回归分类实践

## 我们利用 sklearn 中自带的 iris 数据作为数据载入，并利用Pandas转化为DataFrame格式
from sklearn.datasets import load_iris
data = load_iris() #得到数据特征

iris_target = data.target #得到数据对应的标签
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式

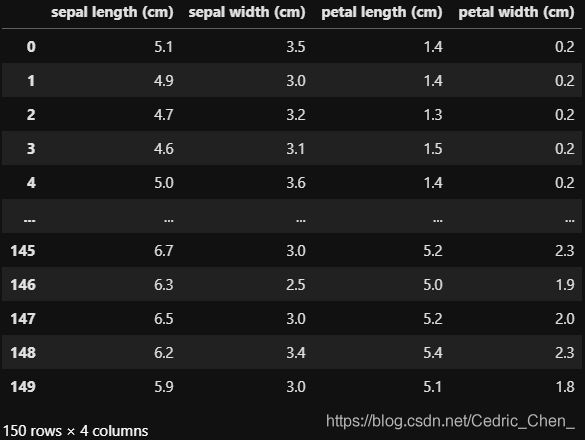
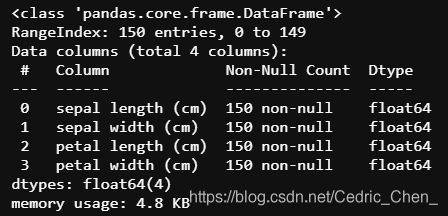
本次我们选择鸢花数据（iris）进行方法的尝试训练，该数据集一共包含5个变量，其中4个特征变量，1个目标分类变量。共有150个样本(各50个)

目标变量为 花的类别 其都属于鸢尾属下的三个亚属，分别是山鸢尾 (Iris-setosa)，变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。

包含的三种鸢尾花的四个特征，分别是花萼长度(cm)、花萼宽度(cm)、花瓣长度(cm)、花瓣宽度(cm)。

变量	描述
sepal length	花萼长度(cm)
sepal width	花萼宽度(cm)
petal length	花瓣长度(cm)
petal width	花瓣宽度(cm)
target	鸢尾的三个亚属类别,‘setosa’(0), ‘versicolor’(1), ‘virginica’(2)

3.1. 查看数据信息

来看看数据集的特征字段长啥样子~~

iris_features

## 利用.info()查看数据的整体信息
iris_features.info()
## 其对应的类别标签为，其中0，1，2分别代表'setosa', 'versicolor', 'virginica'三种不同花的类别。
iris_target
## 利用value_counts函数查看每个类别数量
pd.Series(iris_target).value_counts()

## 对于特征进行一些统计描述,从统计描述中我们可以看到不同数值特征的变化范围。
iris_features.describe()

3.2. 模型的可视化描述

## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝，防止对于原始数据的修改
iris_all['target'] = iris_target  # 添加目标变量列

## 特征与标签组合的散点可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()

从上图可以发现，在平面上不同的特征组合对于不同类别的花的散点分布，以及大概的区分能力。

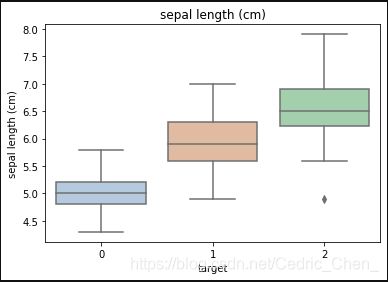
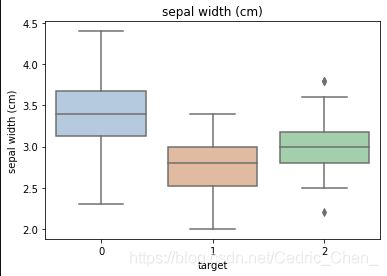
# 箱型图绘制
for col in iris_features.columns:
    sns.boxplot(x='target', y=col, saturation=0.5,palette='pastel', data=iris_all)  # saturation表示颜色区分
    plt.title(col)
    plt.show()

可以看出，类别0【山鸢尾 (Iris-setosa)】较容易区分，而类别1【变色鸢尾(Iris-versicolor)】和类别2【维吉尼亚鸢尾(Iris-virginica)】较难直观区分。

3.3. 利用 逻辑回归模型 在三分类(多分类)上 进行训练和预测————【二分类同理】

## 为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。
from sklearn.model_selection import train_test_split

## 常用20%样本量作为测试集
x_train, x_test, y_train, y_test = train_test_split(iris_features, iris_target, test_size = 0.2, random_state = 2020)
## 参数解释（自变量，因变量，测试集比例，随机数随意设置）

## 创建逻辑回归模型 
clf = LogisticRegression(random_state=0, solver='lbfgs')
''' solver选择解释：
    - 'liblinear' 适用于小样本数据集；'sag'与'saga' 更迅速，适用于数据量较大场景.
    - 多分类场景选择'newton-cg', 'sag', 'saga' 和 'lbfgs'； 'liblinear' 仅适用于双分类需求
    - 'newton-cg', 'lbfgs' 和 'sag'只针对 L2 正则（模型默认penalty=L2）, 而'liblinear' 和'saga' 针对 L1 正则化（需另设参数）
'''

# 在训练集上训练逻辑回归模型
clf.fit(x_train, y_train)

## 查看自变量对应的系数w
print('the weight of Logistic Regression:\n',clf.coef_)

## 查看常数项对应的系数w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)

## 由于这个是3分类场景，所有我们这里得到了三个逻辑回归模型的参数，其三个逻辑回归组合起来即可实现三分类。

## 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)

## 由于逻辑回归模型是概率预测模型（软分类）,所有我们可以利用 predict_proba 函数预测其概率
train_predict_proba = clf.predict_proba(x_train)
test_predict_proba = clf.predict_proba(x_test)

print('The test predict Probability of each class:\n',test_predict_proba)
## 其中第一列代表预测为0类的概率，第二列代表预测为1类的概率，第三列代表预测为2类的概率。

## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression on Train_data is:',metrics.accuracy_score(y_train,train_predict))  # 训练集精度0.958
print('The accuracy of the Logistic Regression on Test_data is:',metrics.accuracy_score(y_test,test_predict))  # 测试集精度0.8


## 在测试集上分类错误的数据一览
contrast = pd.DataFrame()
contrast['origin'] = y_test
contrast['predict'] = test_predict

contrast[contrast['origin'] != contrast['predict']]  

测试集共150*0.2=30个，有6个值分类错误，准确率（24/30=0.8），作为简单分类模型效果还行吧~要啥自行车

来看看基于混淆矩阵的模型评估吧！

3.4. 基于混淆矩阵的模型评估

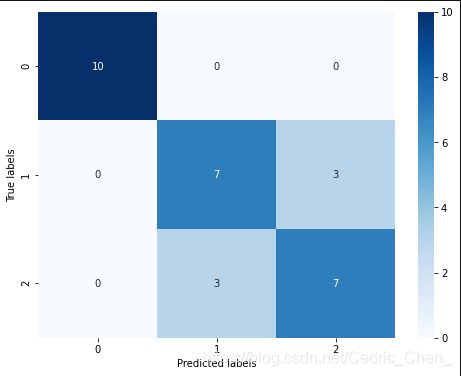
## 查看混淆矩阵
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)  # [[10,3,0],[0,7,3],[0,3,7]]

# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()

通过结果我们可以发现，逻辑回归模型在多分类场景下对结果的预测准确度上有所下降（相比双分类），其在测试集上的准确度为:$80\%$，这是由于类别1【变色鸢尾(Iris-versicolor)】和类别2【维吉尼亚鸢尾(Iris-virginica)】的特征较难区分，同先前箱型图直观观测结果，其特征的边界具有一定的模糊性（边界类别混杂，没有明显区分边界），所有在这两类的预测上出现了一定的错误。

sklearn提供的逻辑回归模型包其实还有很多参数可以设置，关于SIGMOD函数作为神经网络的激活函数的相关内容，这里不再展开

欢迎一起交流讨论~~

END