pytorch使用教程及应用-GANS编程(2)-初步使用pytorch建立神经网络
文章目录
-
-
- 1. 下载数据集
- 2.用pandas处理数据集
- 3.简单的神经网络
-
- 1. 前言
- 2.具体代码实现
- 3.Mnist数据集类
- 4.训练分类器
-
- 完整代码
- 5.检验分类器效果
- 6.完整的测试简单的分类器的性能
-
1. 下载数据集
建立网络的第一步是下载mnist图像数据集到本地,值得注意的是,其应该被下载到和你的pytorch项目在本地的同一文件夹下.
下载地址:
训练数据:https://pjreddie.com/media/files/mnist_train.csv
测试数据:https://pjreddie.com/media/files/mnist_test.csv
数据集是csv格式的,这也是常见数据集的一般格式
2.用pandas处理数据集
pandas DataFrame是一个与numpy数组相似的数据结构,具有许多附加功能。包括可为列和行命名,以及提供遍历函数对数据求和和过滤等。
我们可以使用head()函数查看一个较大DataFrame的前几行。
import torch
import pandas
df=pandas.read_csv('mnist_train.csv',header=None)
print(df.head())#用head函数查看其前五行
df.info()#查看数据集的基本信息,例如该数据集有60000行
output:
0 1 2 3 4 5 6 ... 778 779 780 781 782 783 784
0 5 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
2 4 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
3 1 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
4 9 0 0 0 0 0 0 ... 0 0 0 0 0 0 0
Mnist的每一行数据包含包含785个值。第一个值是图像所表示的数字,
剩余的784个值是图像(尺寸为28像素×28像素)的像素值。
[5 rows x 785 columns]
RangeIndex: 60000 entries, 0 to 59999
Columns: 785 entries, 0 to 784
dtypes: int64(785)
memory usage: 359.3 MB
下面我们来可视化mnist数据集中的一个手写数字
import torch
import pandas
import matplotlib.pyplot as plt
df=pandas.read_csv('mnist_train.csv',header=None)
# print(df.head())
# df.info()
#从DataFrame读取数据
row=0
data=df.iloc[row] #选择数据集的第一行并赋值给变量data data此时为一个数组类型
label=data[0] #第一个值是标签
#图像是余下的784个值
img=data[1:].values.reshape(28,28)
plt.title("label="+str(label))
plt.imshow(img,interpolation='none',cmap='Blues')#指定pyplot无须平滑像素以及指定调色板的颜色为蓝色
plt.show()
你还可以试试通过改变row的值来找到另外一份模拟数字图像
甚至可以为查看这个功能单独编写一个函数
3.简单的神经网络
1. 前言
本次编写神经网络的目的是实现一个神经网络能够识别从mnist数据库提取出的手写数字图像的精确数字,而不需要去用前面使用的label去进行标注。
起始点是一幅mnist数据集中的图像,它的像素个数为28×28=784.
这意味着我们的神经网络的第一层必须有784个节点。
然后在输出层我们可以设计十个结点来分别表示数字0~9,这是一个典型的softmax分类问题,也就是多分类问题。
对于隐藏的中间层,我们有更多的选择。有很多优化神经网络的方法,具体的可以看我其他的博客或者听吴恩达或者其他一些在线的深度学习课程。本篇博文我们会重点关注如何使用pytorch.
此次的中间层我们就先简单设定为200层.
网络中任何一层的所有节点,都会连接到下一层中的所有节点。这种网络也被称为全连接层(fully connected layer)。

激活函数的选择一直都是一个重要的议题,此次神经网络设计我们暂时先采用sigmoid函数(方便快捷),当然实际上还有Relu和Leaky Relu tanh等一系列函数可以供我们选择,关于激活函数的选择也可以找一找我的博文。
2.具体代码实现
创建神经网络类时,我们需要继承pytorch的torch.nn模块。这样一来,新的神经网络就具备了许多pytorch的功能,如自动构建计算图、查看权重以及在训练期间更新权重等。
import torch
import torch.nn as nn
class Classifier(nn.Module):
def __init__(self): #类似于java的构造函数,当我们从一个类中创建对象时其就会自动被调用
#初始化pytorch父类
super.__init__() #继承调用父类的构造函数,然后pytorch.nn模块会为我们设置分类器 一般这个步骤都是必要的,需要通过继承底层的父类的基本属性然后再在后面进行自定义(特定的) 的扩展
#具体的可以查看csdn博客https://blog.csdn.net/a__int__/article/details/104600972
#现在开始设计神经网络,设计神经网络结构有很多种方法
#我们可以使用nn.Sequential(),它允许我们提供了一个网络模块的列表。模块必须按照我们希望的信息传递顺序添加到容器中。
#定义神经网络层
self.model=nn.Sequential(
nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重,在训练时会被更新。
nn.sigmoid,#将S型逻辑函数函数应用于前一个模块的输出,也就是本例中200个节点的输出
nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
nn.sigmoid()#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
)
nn.Linear因何得名?这是因为,当数值从输入端传递到输出端时,该模块对它们应用了Ax+B形式的线性函数。这里,A为链接权重(weights),B为偏差(bias),当然,相信大家都有基本的神经网络知识都了解,这两个参数都被称之为可学习参数(learnable parameter),因为它们可以在训练时被更新。
接下来的任务是定义cost function和参数的优化方法:
- cost function定义
cost function(error function or loss function)一个最为简单的是均方误差(mean squared error)。均分误差先计算每个输出节点的实际输出和预期输出之差的平方,再计算平均值,Pytorch将其定义为torch.nn.MSELoss().
self.loss_function=nn.MSELoss()
- 优化方法选择(这里选择最简单的随机梯度下降 SGD)–什么是随机梯度下降可以查看我的其他博客有详细介绍,其是mini-batch gradient descent 的一个极端情况
self.optimiser=torch.optim.SGD(self.parameters(),lr=0.01) #创建优化器,使用简单的梯度下降,设定学习率为0.01
- 定义前向传播函数
pytorch需要在模型类里面创建一个forward方法,其可以非常简短;
关于forward函数的理解,可以查看博客 https://blog.csdn.net/xu380393916/article/details/97280035 https://blog.csdn.net/u011501388/article/details/84062483
forward函数我们每次设计神经网络的时候都是必须使用的,官方要求我们自定义module的时候必须覆写该方法.
def forward(self,inputs):
#直接运行模型
return self.model(inputs)
我们将输入传递给self.mode(),它由nn.Sequential()定义,模型的输出直接返回给forward()的主调函数。
目前为止的进展是:
1. 通过继承nn.Module,我们创建了一个神经网络类。它从nn.Module中继承了训练神经网络所需的大部分功能。
2. 我们定义了处理信息的神经网络模块。对于简单的神经网络,我们选择使用精简的nn.Sequential方法。
3. 我们定义了成本函数和更新网络可学习参数的优化器。
4. 最后,我们添加了一个forward()函数,Pytorch会通过它将信息传递给网络。
import torch
import torch.nn as nn
class Classifier(nn.Module):
def __init__(self): #类似于java的构造函数,当我们从一个类中创建对象时其就会自动被调用
#初始化pytorch父类
super().__init__() #继承调用父类的构造函数,然后pytorch.nn模块会为我们设置分类器 一般这个步骤都是必要的,需要通过继承底层的父类的基本属性然后再在后面进行自定义(特定的) 的扩展
#现在开始设计神经网络,设计神经网络结构有很多种方法
#我们可以使用nn.Sequential(),它允许我们提供了一个网络模块的列表。模块必须按照我们希望的信息传递顺序添加到容器中。
#定义神经网络层
self.model=nn.Sequential(
nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重,在训练时会被更新。
nn.Sigmoid,#将S型逻辑函数函数应用于前一个模块的输出,也就是本例中200个节点的输出
nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
nn.Sigmoid()#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
)
#创建损失函数
self.loss_function=nn.MSELoss()
#创建优化器,使用简单的梯度下降
self.optimiser=torch.optim.SGD(self.parameters(),lr=0.01)
pass #Python pass 是空语句,是为了保持程序结构的完整性。
#pass 不做任何事情,一般用做占位语句。
def forward(self,inputs):
#直接运行模型
return self.model(inputs)
接下来,我们需要想办法来训练这个网络
我们不需要一个像forward()一样的train()函数,pytorch允许我们按照自己的想法构建网络的训练代码。
但是为了代码更加好看,我们选择与forward()函数保持一致,创建一个train()函数。
train()即需要网络的输入值,也需要预期的目标值。这样才可以与实际输出进行比较,并计算损失值。
代码实现:
def train(self,inputs,targets):
# 计算网络的输出值
outputs=self.forward(inputs)
# 计算 cost
loss=self.loss_function(outputs,targets)
#pytorch简化了我们自己造轮子时需要为每个节点计算误差梯度,再更新链接权值。
# 梯度归零,反向传播,并更新权重
self.optimiser.zero_grad() #将计算图中的梯度全部归0,也就是我们的初始化
loss.backward() #从loss函数中反向传播计算梯度
self.optimiser.step() #使用这些梯度来更新网络的可学习参数
#在每次训练网络之前,我们都需要将梯度归零。否则,每次loss.backward()计算出来的梯度会累积。
可视化训练:
使用可视化训练的方式,我们实时监控到目前网络优化的效果,可以知道目前的迭代优化进行得是否顺利。
在train()里面,我们在每次计算损失值时,将副本保存在一个列表里。这意味着该表会变得非常大,因为训练神经网络通过会允许成千上万、甚至百万个样本。MNist数据集有60000个训练样本,且我们需要遍历几次(epoch)。 所以,我们设计为在每完成10个训练样本之后保留一份损失副本。所以,我们还需要记录train()的运行频率。
#记录训练进展的计数器和列表
self.counter=0
self.progress=[]
#在train()函数中,我们可以每隔10个训练样本增加一次计数器的值,并将损失值添加进列表的末尾。
#每隔10个训练样本增加一次计数器的值,并将损失值添加进列表的末尾
self.counter += 1
if(self.counter%10 ==0):
self.progress.append(loss.item()) #item函数方便我们展开一个单值张量,获取里面的数字
pass
#方便了解训练目前的进展快慢
if(self.counter%10000==0):
print("counter =",self.counter)
pass
#将损失值可视化绘制成图,我们可以在神经网络类中添加一个新函数plot_progress()
def plot_progress(self):
df=pandas.DataFrame(self.progress,columns=['loss']) #将损失值列表progress转换成一个pandas DataFrame对象
df.plot(ylim=(0,1.0),figsize=(16,8),alpha=0.1,marker='.', #使用plot()函数的选项,设计图的设计和风格
grid=True,yticks=(0,0.25,0.5))
pass
3.Mnist数据集类
用pandas读取数据集自然是不错的选择,但我们现在在学习pytorch,还是应该去学习使用pytorch独特的方式去读取和处理数据。
Pytorch使用torch.utils.data.DataLoader实现了一些实用的功能,比如自动打乱数据顺序、多个进程并行加载、分批处理等,但这都需要先将数据载入一个torch.utils.Dataset对象。
from torch.utils.data import Dataset
和我们从nn.Module继承一个神经网络类时需要覆写forward()方法一样,同样地,对于继承自Dataset的数据集,我们需提供以下两个特殊的函数。
__len__(), 返回数据集中的项目总数
__getitem__(), 返回数据集中的第n项
接下来,我们会创建一个MnistDataset类,并提供__len__()方法,允许Pytorch通过len(mnist_dataset)获取数据集的大小。同时,我们也会提供getitem__(),允许我们通过索引获取项目,例如使用mnist_dataset[3]访问第四项这样子
上源码:
import torch
import torch.nn as nn
import pandas
import matplotlib.pyplot as plt
from torch.utils.data import Dataset
class MnistDataset(Dataset):
def __init__(self,csv_file):
self.data_df=pandas.read_csv(csv_file,header=None)
pass
def __len__(self):
return len(self.data_df)
def __getitem__(self, index):
#目标图像(标签)
label=self.data_df.iloc[index,0] #从数据集中的第index项中提取该数字的标签-也就是该数字具体是多少
targets=torch.zeros((10)) #初始化都为0,最后的结果应该为除了与标签相对应的项是1之外,其他值皆为0.比如,标签0所对应的张量是[1,0,0,0,0,0,0,0,0,0] 这种表示方法叫做 one-hot encoding
targets[label]=1.0
#图像数据,取值范围是0~255,标准化为0~1
image_values=torch.FloatTensor(self.data_df.iloc[index,1:].values)/255.0 #将图像像素值标准化
#返回标签、图像数据张量以及目标张量
return label,image_values,targets
#添加一个可视化函数
def plot_image(self,index):
arr=self.data_df.iloc[index,1:].values.reshape(28,28)
plt.title("label="+str(self.data_df.iloc[index,0]))
plt.imshow(arr,interpolation='none',cmap='Blues')
plt.show()
pass
pass
if __name__ == '__main__':
mnist_dataset=MnistDataset('mnist_train.csv')
print(mnist_dataset[2]) #注意两个函数的顺序,画图一般在后
mnist_dataset.plot_image(9)
//
output: (4, tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.2627, 0.9098,
0.1529, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.2431, 0.3176, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.4706,
0.7059, 0.1529, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.4941, 0.6392, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0078,
0.6000, 0.8235, 0.1569, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.8627, 0.6392, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.1059, 0.9961, 0.6353, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.8706, 0.6392, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.7176, 0.9961, 0.4902, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.1804, 0.9608, 0.6392, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.7765, 0.9961, 0.2196, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.4706, 0.9961, 0.6392, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0902, 0.9059, 0.9961, 0.1137, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.6235, 0.9961, 0.4706,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.6392, 0.9961, 0.8471, 0.0627, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.6235, 0.9961,
0.2627, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0549, 0.3373, 0.6980, 0.9725, 0.9961, 0.3569, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.6235,
0.9961, 0.3333, 0.0000, 0.0000, 0.0000, 0.1843, 0.1922, 0.4549, 0.5647,
0.5882, 0.9451, 0.9529, 0.9176, 0.7020, 0.9451, 0.9882, 0.1569, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.5882, 0.9922, 0.9294, 0.8118, 0.8118, 0.8118, 0.9922, 0.9961, 0.9804,
0.9412, 0.7765, 0.5608, 0.3569, 0.1098, 0.0196, 0.9137, 0.9804, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.4667, 0.6941, 0.6941, 0.6941, 0.6941, 0.6941, 0.3843,
0.2196, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.4000, 0.9961, 0.8627,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.6627, 0.9961,
0.5373, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.6627,
0.9961, 0.2235, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.6627, 0.9961, 0.2235, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.6627, 1.0000, 0.3686, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.6627, 0.9961, 0.3765, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.6627, 0.9961, 0.6000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.6627, 1.0000, 0.6000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.3765, 0.9961, 0.6000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000]), tensor([0., 0., 0., 0., 1., 0., 0., 0., 0., 0.]))
Process finished with exit code 0
经过测试,我们的可视化数据集已经编写成功
4.训练分类器
我们在前面已经完成了复杂的工作,定义数据集类和神经网络类。
现在我们开始训练分类器softmax
if __name__ == '__main__':
#创建神经网络
C=Classifier()
#训练网络的代码同样很简单:
#在Mnist数据集训练神经网络
for label,image_data_tensor,target_tensor in mnist_dataset :
C.train(image_data_tensor,target_tensor)
pass
mnist_dataset继承了pytorch Dataset,它允许我们使用for循环遍历所有训练数据。对于每个样本,我们只将图像数据和目标张量传递给分类器的train()方法。SGD方法每次训练就是只要一个样本
当然,我们可以多次遍历数据集,只需要在训练循环周围添加一个外部周期循环即可,这有利于我们进一步优化我们的神经网络
实际训练上,我们会使用矩阵的方法一次遍历多个训练样本,这叫做mini-batch 梯度下降,大家感兴趣的可以看看我的其他博客。
当然,现在是处于学习阶段,我们可以添加一个程序计时器,这样方便我们进行复盘,也可以估计出大概的时间为以后的实验打好基础,在以后的实验过程中我们就可以算好时间去刷B站了,回来再看结果,对吧。
完整代码
import torch
import torch.nn as nn
import pandas
import time
import matplotlib.pyplot as plt
from torch.utils.data import Dataset
class Classifier(nn.Module):
def __init__(self): #类似于java的构造函数,当我们从一个类中创建对象时其就会自动被调用
#初始化pytorch父类
super().__init__() #继承调用父类的构造函数,然后pytorch.nn模块会为我们设置分类器 一般这个步骤都是必要的,需要通过继承底层的父类的基本属性然后再在后面进行自定义(特定的) 的扩展
#现在开始设计神经网络,设计神经网络结构有很多种方法
#我们可以使用nn.Sequential(),它允许我们提供了一个网络模块的列表。模块必须按照我们希望的信息传递顺序添加到容器中。
#定义神经网络层
self.model=nn.Sequential(
nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重,在训练时会被更新。
nn.Sigmoid(),#将S型逻辑函数函数应用于前一个模块的输出,也就是本例中200个节点的输出
nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
nn.Sigmoid()#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
)
self.loss_function = nn.MSELoss()
# 创建优化器,使用简单的梯度下降
self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)
# 记录训练进展的计数器和列表
self.counter = 0
self.progress = []
pass # Python pass 是空语句,是为了保持程序结构的完整性。
# pass 不做任何事情,一般用做占位语句。
pass
def forward(self,inputs):
#直接运行模型
return self.model(inputs)
def train(self,inputs,targets):
# 计算网络的输出值
outputs=self.forward(inputs)
# 计算 cost
loss=self.loss_function(outputs,targets)
#pytorch简化了我们自己造轮子时需要为每个节点计算误差梯度,再更新链接权值。
# 梯度归零,反向传播,并更新权重
self.optimiser.zero_grad() #将计算图中的梯度全部归0,也就是我们的初始化
loss.backward() #从loss函数中反向传播计算梯度
self.optimiser.step() #使用这些梯度来更新网络的可学习参数
#在每次训练网络之前,我们都需要将梯度归零。否则,每次loss.backward()计算出来的梯度会累积。
#在train()函数中,我们可以每隔10个训练样本增加一次计数器的值,并将损失值添加进列表的末尾。
#每隔10个训练样本增加一次计数器的值,并将损失值添加进列表的末尾
self.counter += 1
if(self.counter%10 ==0):
self.progress.append(loss.item()) #item函数方便我们展开一个单值张量,获取里面的数字
pass
#方便了解训练目前的进展快慢
if(self.counter%10000==0):
print("counter =",self.counter)
pass
# 将损失值可视化绘制成图,我们可以在神经网络类中添加一个新函数plot_progress()
def plot_progress(self):
df = pandas.DataFrame(self.progress, columns=['loss']) # 将损失值列表progress转换成一个pandas DataFrame对象
df.plot(ylim=(0, 1.0), figsize=(16, 8), alpha=0.1, marker='.', # 使用plot()函数的选项,设计图的设计和风格
grid=True, yticks=(0, 0.25, 0.5))
plt.show()
pass
class MnistDataset(Dataset):
def __init__(self,csv_file):
self.data_df=pandas.read_csv(csv_file,header=None)
pass
def __len__(self):
return len(self.data_df)
def __getitem__(self, index):
#目标图像(标签)
label=self.data_df.iloc[index,0] #从数据集中的第index项中提取该数字的标签-也就是该数字具体是多少
targets=torch.zeros((10)) #初始化都为0,最后的结果应该为除了与标签相对应的项是1之外,其他值皆为0.比如,标签0所对应的张量是[1,0,0,0,0,0,0,0,0,0] 这种表示方法叫做 one-hot encoding
targets[label]=1.0
#图像数据,取值范围是0~255,标准化为0~1
image_values=torch.FloatTensor(self.data_df.iloc[index,1:].values)/255.0 #将图像像素值标准化
#返回标签、图像数据张量以及目标张量
return label,image_values,targets
#添加一个可视化函数
def plot_image(self,index):
arr=self.data_df.iloc[index,1:].values.reshape(28,28)
plt.title("label="+str(self.data_df.iloc[index,0]))
plt.imshow(arr,interpolation='none',cmap='Blues')
plt.show()
pass
pass
if __name__ == '__main__':
mnist_dataset=MnistDataset('mnist_train.csv')
t0=time.time()
#创建神经网络
C=Classifier()
#训练网络的代码同样很简单:
#在Mnist数据集训练神经网络
epochs=3
for i in range(epochs):
print('training epoch',i+1,"of",epochs)
for label,image_data_tensor,target_tensor in mnist_dataset:
C.train(image_data_tensor,target_tensor)
pass
C.plot_progress() #绘制可视化训练图 一般来说 python遇到绘图代码时运行会发生停顿,这是正常的,需要多耐心等待一下
print('一个周期的训练耗费了'+str(time.time()-t0)+'s')
pass
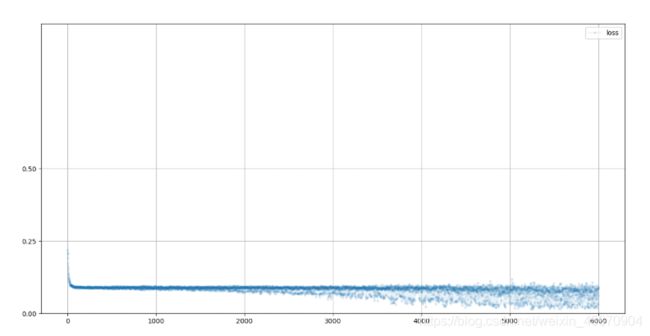
训练过程截图:
训练神经网络存在一定的随机性。
结论:
-
从上图可见,损失值从一开始迅速下降到大约0.1,并在训练过程中越来越慢地去接近0.但是同时,也可以看到,后面的训练存在很多噪声,或者说振荡。大家可以进一步去了解凸优化和梯度下降的过程,就能够明白为什么会发生这种震荡。
-
损失值的下降意味着网络分类图像的能力越来越好。
-
损失图实用性很高,他能够让我们去了解到网络训练是否有效,而且还能让我们指导训练过程是平稳的,还是不稳定和混乱的。
5.检验分类器效果
先附上最新的完整代码:
import torch
import torch.nn as nn
import pandas
import time
import matplotlib.pyplot as plt
from torch.utils.data import Dataset
class Classifier(nn.Module):
def __init__(self): #类似于java的构造函数,当我们从一个类中创建对象时其就会自动被调用
#初始化pytorch父类
super().__init__() #继承调用父类的构造函数,然后pytorch.nn模块会为我们设置分类器 一般这个步骤都是必要的,需要通过继承底层的父类的基本属性然后再在后面进行自定义(特定的) 的扩展
#现在开始设计神经网络,设计神经网络结构有很多种方法
#我们可以使用nn.Sequential(),它允许我们提供了一个网络模块的列表。模块必须按照我们希望的信息传递顺序添加到容器中。
#定义神经网络层
self.model=nn.Sequential(
nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重,在训练时会被更新。
nn.Sigmoid(),#将S型逻辑函数函数应用于前一个模块的输出,也就是本例中200个节点的输出
nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
nn.Sigmoid()#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
)
self.loss_function = nn.MSELoss()
# 创建优化器,使用简单的梯度下降
self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)
# 记录训练进展的计数器和列表
self.counter = 0
self.progress = []
pass # Python pass 是空语句,是为了保持程序结构的完整性。
# pass 不做任何事情,一般用做占位语句。
pass
def forward(self,inputs):
#直接运行模型
return self.model(inputs)
def train(self,inputs,targets):
# 计算网络的输出值
outputs=self.forward(inputs)
# 计算 cost
loss=self.loss_function(outputs,targets)
#pytorch简化了我们自己造轮子时需要为每个节点计算误差梯度,再更新链接权值。
# 梯度归零,反向传播,并更新权重
self.optimiser.zero_grad() #将计算图中的梯度全部归0,也就是我们的初始化
loss.backward() #从loss函数中反向传播计算梯度
self.optimiser.step() #使用这些梯度来更新网络的可学习参数
#在每次训练网络之前,我们都需要将梯度归零。否则,每次loss.backward()计算出来的梯度会累积。
#在train()函数中,我们可以每隔10个训练样本增加一次计数器的值,并将损失值添加进列表的末尾。
#每隔10个训练样本增加一次计数器的值,并将损失值添加进列表的末尾
self.counter += 1
if(self.counter%10 ==0):
self.progress.append(loss.item()) #item函数方便我们展开一个单值张量,获取里面的数字
pass
#方便了解训练目前的进展快慢
if(self.counter%10000==0):
print("counter =",self.counter)
pass
# 将损失值可视化绘制成图,我们可以在神经网络类中添加一个新函数plot_progress()
def plot_progress(self):
df = pandas.DataFrame(self.progress, columns=['loss']) # 将损失值列表progress转换成一个pandas DataFrame对象
df.plot(ylim=(0, 1.0), figsize=(16, 8), alpha=0.1, marker='.', # 使用plot()函数的选项,设计图的设计和风格
grid=True, yticks=(0, 0.25, 0.5))
plt.show()
pass
class MnistDataset(Dataset):
def __init__(self,csv_file):
self.data_df=pandas.read_csv(csv_file,header=None)
pass
def __len__(self):
return len(self.data_df)
def __getitem__(self, index):
#目标图像(标签)
label=self.data_df.iloc[index,0] #从数据集中的第index项中提取该数字的标签-也就是该数字具体是多少
targets=torch.zeros((10)) #初始化都为0,最后的结果应该为除了与标签相对应的项是1之外,其他值皆为0.比如,标签0所对应的张量是[1,0,0,0,0,0,0,0,0,0] 这种表示方法叫做 one-hot encoding
targets[label]=1.0
#图像数据,取值范围是0~255,标准化为0~1
image_values=torch.FloatTensor(self.data_df.iloc[index,1:].values)/255.0 #将图像像素值标准化-很重要的一步
#返回标签、图像数据张量以及目标张量
return label,image_values,targets
#添加一个可视化函数
def plot_image(self,index):
arr=self.data_df.iloc[index,1:].values.reshape(28,28)
plt.title("label="+str(self.data_df.iloc[index,0]))
plt.imshow(arr,interpolation='none',cmap='Blues')
plt.show()
pass
pass
if __name__ == '__main__':
mnist_dataset=MnistDataset('mnist_train.csv')
mnist_test_dataset=MnistDataset('mnist_test.csv') #mnist_test_dataset有1万条数据
t0=time.time()
count=0
#创建神经网络
C=Classifier()
#训练网络的代码同样很简单:
#在Mnist数据集训练神经网络
epochs=3
for i in range(epochs):
print('training epoch',i+1,"of",epochs)
for label,image_data_tensor,target_tensor in mnist_dataset:
C.train(image_data_tensor,target_tensor)
pass
print(str(count+1)+'个周期的训练耗费了'+str(time.time()-t0)+'s')
count+=1
pass
record=19
image_data=mnist_test_dataset[record][1] #默认使用getitem方法 该方法已被覆写
output=C.forward(image_data)
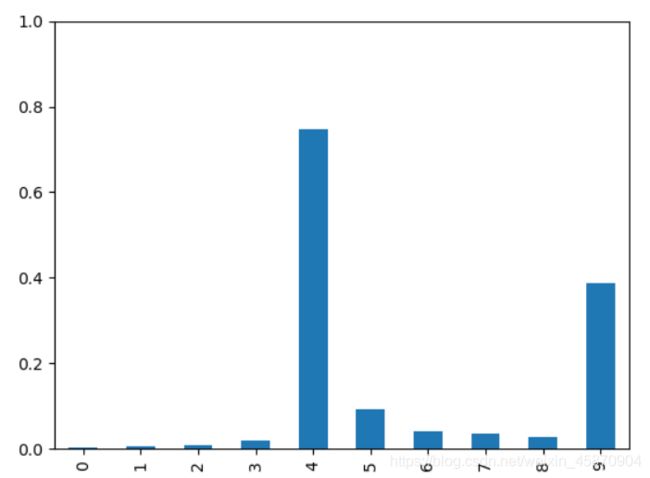
pandas.DataFrame(output.detach().numpy()).plot(kind='bar',legend=False,ylim=(0,1))
plt.show()
大家都知道,对于逻辑回归,我们的输出函数使用的是sigmoid(),而多分类,当然也是使用的sigmoid(),使用one-hot-code格式,但是我们这里并不是采用的在最后接softmax层的方法,而只是简单的深层神经网络方法。而使用sigmoid()函数,也意味着我们输出的是该东西为1的概率。p(y=1),而多分类,输出的当然就是等于各个可能结果的概率。
大家如果想要仔细了解logistic regression和softmax还有两个损失函数(不同)
可以看看这篇知乎:https://www.zhihu.com/question/341500352/answer/795497527
希望大家能分清楚什么是单(标签)(多)分类交叉熵和多标签分类交叉熵
最后,我们检测4这个数字,发现网络认为该数字为4的概率大于9,这说明,我们的网络训练取得了不错的成效。但是我们也必须清楚,神经网络大多是存在误差的,例如对于比较潦草的数字,像素值有偏差的,就容易出现识别错误的现象。
6.完整的测试简单的分类器的性能
接下来我们来完整地测试一下我们模型的性质,我们使用一种比较直接的方法,对MNIST测试数据集中所有10000幅图像进行分类,并记录正确分类的样本数。
分类是否正确可以通过比较网络输出和图像的标签来分辨。
#测试用训练数据训练后的网络
score=0
items=0
for label,image_data_tensor,target_tensor in mnist_test_dataset:
answer=C.forward(image_data_tensor).detach().numpy()
#argmax返回向量中最大值的索引
if (answer.argmax()==label):
score+=1
pass
items+=1
pass
print(score,items,score/times)