散列表(hash table)是实现字典操作的一种有效数据结构,尽管最坏情况下,散列表中的查找一个元素的时间与链表中的查找时间相同,达到了Θ(n),在合理的假设查找一个元素的平均时间为Θ(1)。
散列表的本质还是普通数组概念的推广。在散列表中不是直接关键字作为数组的下标,而是 根据关键字计算出相应的下标。
1.直接寻址法
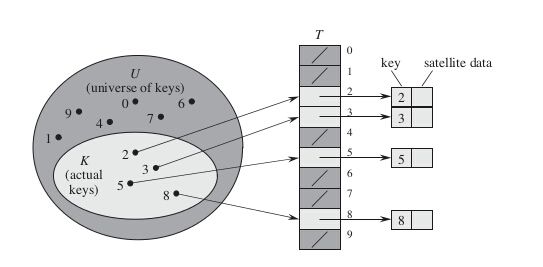
当关键字的的全域(范围)U比较小的时,直接寻址是简单有效的技术,一般可以采用数组实现直接寻址表,数组下标对应的就是关键字的值,即具有关键字k的元素被放在直接寻址表的槽k中。直接寻址表的字典操作实现比较简单,直接操作数组即可以,只需O(1)的时间。见下图:
设T为一个动态集合,其中每个元素都是取自全域U={0,1,...,m-1}中的一个关键字,这里m不是一个很大的数。另外,假设没有两个元素具有相同的关键字。
为表示动态集合,我们用一个数组,或称为直接寻址表(direct-address table),记为T[0...m-1]。其中每个位置,称为一个槽(slot),对应全域U中的一个关键字。上图描述了该方法。槽k指向集合中一个关键字为k的元素。如果该集合中没有关键字为k的元素,则T[k]为NIL
2、散列寻址
(1)直接寻址法的缺点
直接寻址技术的缺点是非常明显的:如果全域U很大,则在一台标准的计算机可用内存容量中,要存储大小为|U|的一张表T也许不大实际,甚至不可能。还有,实际存储的关键字集合K相对于U来说可能很小,使得分配给T的大部分空间都将浪费掉
(2)散列表
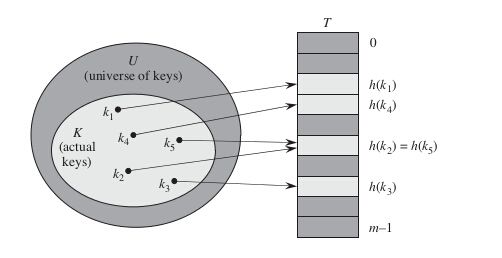
当存储在字典中的关键字集合K比所有可能的关键字的全域U要小许多时,散列表需要的存储空间要比直接寻址表少的多。在散列方式下,元素存放在槽h(k)中即利用散列函数h,由关键字k计算出槽的位置。这里,函数h将关键字的全域U映射到散列表T[0...m-1]的槽位上,如下图所示
-
散列函数:在散列的方式下,该元素存放在槽h(k)中,即h为散列函数 -
散列值: 具体关键字k的元素被散列到槽h(k),即h(k)是关键字k的散列值 -
冲突:两个关键字可能映射到同一槽中,这种情形为冲突(collision) -
解决冲突的方法:链表法和开放寻址法,其中开放寻址法又有几种可选的方法:线性探查、二次探查、双重散列
3、散列函数
- 好的散列函数的特点:
每个关键字都等可能的散列到m个槽位上的任何一个中去,并与其他的关键字已被散列到哪一个槽位无关。- 将关键字转换为自然数 :
多数散列函数都是假定关键字域为自然数N={0,1,2,....},如果给的关键字不是自然数,则必须有一种方法将它们解释为自然数。
例如对关键字为字符串时,可以通过将字符串中每个字符的ASCII码相加,转换为自然数。
下面开始介绍几种散列函数:
(1)除法散列
通过取k除以m的余数,将关键字k映射到m个槽的某一个中去。散列函数为:h(k)=k mod m。m不应是2的幂,通常m的值是与2的整数幂不太接近的质数。
下面的数如何通过除法散列映射到具有11个槽的散列表中:23,346
通过除法散列:
23 % 11 = 1(余数是1)
346 % 11 = 5(余数是5)
则应该插入到1,5槽中
(2)乘法散列
乘法散列法构造散列函数需要两个步骤。第一步,用关键字k乘上常数A(0
这里我暂时不是很理解,后面有机会在解答。
(3)全域散列
任何一个特定的散列函数都可能将特定的n个关键字全部散列到同一个槽中,使得平均的检索时间为Θ(n)。为了避免这种情况,唯一有效的改进方法是随机地选择散列函数,使之独立与要存储的关键字。这种方法称为全域散列(universal hashing)
全域散列在执行开始时,就从一组精心设计的函数中,随机地选择一个作为散列函数。因为随机地选择散列函数,算法在每一次执行时都会有所不同,甚至相同的输入都会如此。这样就可以确保对于任何输入,算法都具有较好的平均情况性能.
选择一个足够大的质数p,使得每一个可能的关键字都落在0到p-1的范围内。设Zp表示集合{0, 1, …, p-1},Zp表示集合{1, 2, …, p-1}。对于任何a∈Zp和任何b∈Zp,定义散列函数有:
ha,b (k)= ((ak+b) mod p) mod m;其中a,b是满足自己集合的随机数;
例如,如果p=17,m=6,则h3,4 (8) =(3*8+4)mod17mod6 =5
(4)完全散列
如果某种散列技术可以在查找时,最坏情况内存访问次数为O(1)的话,则称其为完全散列(perfect hashing)。当关键字集合是静态的时,这种最坏情况的性能是可以达到的。所谓静态就是指一旦各关键字存入表中后,关键字集合就不再变化了。
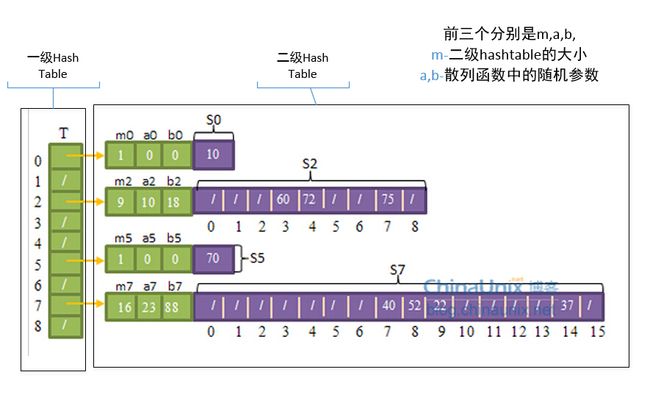
我们可以用一种两级的散列方案来实现完全散列,其中每级上采用的都是全域散列。如下图:
首先第一级使用全域散列把元素散列到各个槽中,这与其它的散列表没什么不一样。但在处理碰撞时,并不像链接法(碰撞处理方法)一样使用链表,而是对在同一个槽中的元素再进行一次散列操作。也就是说,每一个(有元素的)槽里都维护着一张散列表,该表的大小为槽中元素数的平方,例如,有3个元素在同一个槽的话,该槽的二级散列表大小为9。不仅如此,每个槽都使用不同的散列函数,在全域散列函数簇h(k) = ((a*k+b) mod p) mod m中选择不同的a值和b值,但所有槽共用一个p值如101。每个槽中的(二级)散列函数可以保证不发生碰撞情况。
可 以证明,当二级散列表的大小为槽内元素数的平方时,从全域散列函数簇中随机选择一个散列函数,会产生碰撞的概率小于1/2。所以每个槽随机选择散列函数后,如果产生了碰撞,可以再次尝试选择其它散列函数,但这种尝试的次数是非常少的。
虽然二级散列表的大小要求是槽内元素数的平方,看起来很大,但可以证明,当散列表的槽的数量和元素数量相同时(m=n),所有的二级散列表的大小的总量的期望值会小于2n,即Ө(n)。
5、碰撞处理方法
下面介绍几种冲突解决的方法,主要包括链表法和开放寻址法。其中开放寻址法又有几种可选的方法:线性探查、二次探查、双重散列、随机散列
(1)链表法
在链接法中,把散列到同一槽中的所有元素(冲突的元素)都放在一个链表中;
若选定的散列表长度为m,则可将散列表定义为一个由m个头指针组成的指针数组T[0..m-1]。凡是散列地址为i的结点,均插入到以T[i]为头指针的单链表中。T中各分量的初值均应为空指针。在拉链法中,装填因子α可以大于1,但一般均取α≤1。
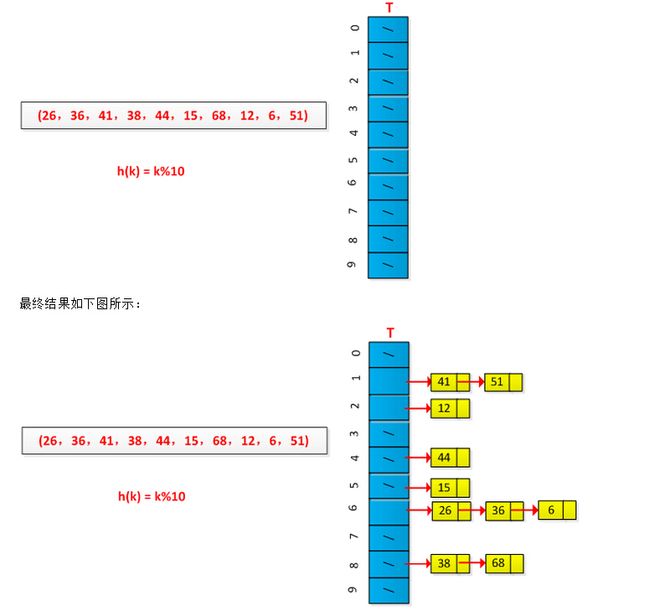
举例说明链接法的执行过程,设有一组关键字为(26,36,41,38,44,15,68,12,6,51),用除余法构造散列函数,初始情况如下图所示:
装载因子
给定一个能存放n个元素的,具有M个槽位的散列表T,定义T的装载因子 a = n/m
性能分析
最坏的情况是:
n个关键字都散列到了一个槽中,从而产生了一个长度为n链表,于是查找的时间为:Θ(n)平均性能:
假设关键字是均匀散列的,第一步是计算散列值h(k),第二步是从根据链表找到相应的关键字的值。第一步所花的时间为:Θ(1),总的时间由下面的定理决定,证明省略
- 定理1: 在简单均匀散列的假设下,对于用链接法解决冲突的散列表,一次
不成功的查找的平均时间为Θ(1+a)- 定理2: 在简单均匀散列的假设下,对于用链接法解决冲突的散列表,一次
成功的查找的平均时间为Θ(1+a)
(2)开放寻址法
开放寻址法是另外一个处理元素冲突的方法;链表法是把冲突的元素依次放到一串链表中,而开放寻址法的思路是:在产生冲突的情况下,在hashtable中寻找其他空闲的槽位插入;当然,如何寻找其他空闲的槽位,我们有几种方法,包括:线性探查、二次探查、双重散列;下面逐个讲解。
线性探查
给定一个普通的散列函数h':U-->{0,1,...,m-1},称为辅助散列函数,线性探查方法采用的散列函数为
h(k,i)=(h'(k)+i) mod m, i = 0,1,...,m-1
给定一个关键字k,首先探查槽T[h'(k)],即由辅助三列函数所给出的槽位。再探测T[h'(k)+1],依次类推,直到槽T[m-1]。然后,又绕到槽T[0],T[1],...,直到最后探测到槽T[h'(k)-1]。
线性探测方法比较容易实现,但它存在着一个问题,称为一次群集。随着连续被占用的槽不断增加,平均查找时间也随之不断增加。集群现象很容易出现,这是因为当一个空槽前有i个满的槽时,该空槽下一个将被占用的概率是(i+1)/m。连续被占用的槽就会变得越来越长,因而平均查询时间也会越来越大
二次探查
h(k,i)=(h'(k)+c₁i+c₂i²) mod m , 其中 i = 0,1,...,m-1
其中h'是一个辅助散列函数,c₁和c₂为正的辅助常数,i=0,1,...m-1。初始的探查位置为T[h'(k)],后续的探查位置要加上一个偏移量,该偏移量以二次的方式依赖于探查序号i。这种探查方法的效果要比线性探查好很多,但是,为了能够充分利用散列表,c₁,c₂和m的值要受到限制。
此外,如果两个关键字的初始探查位置相同,那么它们的探查序列也是相同的。这一性质可导致一种轻度的群集,称为二次群集。
双重散列
双重散列(double hashing)是用于开放寻址法的最好方法之一,因为它所产生的排列具有随机选择队列的许多特性。双重散列采用如下形式的散列函数:
h(k,i)=(h₁(k)+ih₂(k)) mod m, 其中 i = 0,1,...,m-1
其中h₁和h₂均为辅助散列函数。初始探查位置为T[h₁(k)],后续的探查位置是前一个位置加上偏移量h₂(k)模m。因此,不像线性探查或二次探查,这里的探查序列以两种不同方式依赖于关键字k,因为初始探查位置、偏移量或者两则都可能发生变化。下图给出了一个使用双重散列法进行插入的例子。
上图说明:双重散列法的插入。此处,散列表的大小为13,h₁(k)=k mod13,h₂(k)=1+(k mod 11)。以元素14为例:因为h₁(14)=(14 mod13)=1,槽1已被79占用,--》h₂(14)=1+(14 mod 11)=4,则h(14,1)=h₁(14)+h₂(14)=1+4=5,槽5已被98占用,--》h(14,2)=h₁(14)+2h₂(14)=1+24=9,槽9空闲,则插入到槽9中;所以在探查了槽1和槽5,并发现它们被占用后,关键字14插入了槽9中
6、再散列问题
如果散列表满了,再往散列表中插入新的元素时候就会失败;或者散列表快满时,进行插入是一个效率很低的过程;这个时候可以通过创建另外一个散列表,使得新的散列表的长度是当前散列表的2倍多一些,重新计算各个元素的hash值,插入到新的散列表中。再散列的问题是在什么时候进行最好,有下面情况可以判断是否该进行再散列:
(1)当散列表将快要满了,给定一个范围,例如散列被中已经被用到了80%,这个时候进行再散列。
(2)当插入一个新元素失败时候(相同关键字失败除外),进行再散列。
(3)当插入一个新元素产生冲突次数过多时,进行再散列。
(3)对于链表法,根据装载因子(已存放n个元素的、具有m个槽位的散列表T,装载因子α=n/m)进行判断,当装载因子达到一定的阈值时候,进行再散列。
7、代码演示
后面有机会讲解jdk中 HashMap的源码实现
7、参考资料:
https://www.cnblogs.com/zhoutaotao/p/4067749.html#yinyan