第七周课程总结

区间DP：尽管很多题目都听懂了，看着代码也能理解，但是对于状态转移的具体过程事实上大多数只停留在代码，转移过程并不清晰，因此要加强状态转移的理解。

课上重点例题
题意：一群男生上台，每人都有一个紧张值，和出场顺序k有关（a[i]*(k-1)),有一个小黑屋调整出场顺序，相当于栈，先进后出，求最小的紧张值的和最小。
题目本身感觉就很难，上课也只是大致听懂了个思路
收获：
1.一个问题放在一个大区间内很难想，可以在先在小区间内模拟。本题会出现一个问题，小区间内的模拟会出现一些无效区间---->>>通常将无效区间定为0，而由于本题是求最小值，所以又要求将某些区间设定为无穷大。
到此，对区间的初始化才完成（初始化通常是做dp的第一步，有很多种情况，也是一个难点）
2.状态转移方程很难找，很复杂。脑子里想：会想到有很多人需要调换顺序的情况，以及调换到哪个位置紧张之最小，都很难处理。
问题解决：
很多人需要调换----->>>首先要明白这是一个大问题，可分解为有很多规模小的子问题（DP特征）。也就是先考虑小区间内人员调换最优情况，小规模的人员调动。最后大问题（很多人需要调动的最优）便分解为多个小区间内最优情况的累加。
（不要有畏难情绪，不去深思永远都是难题。）
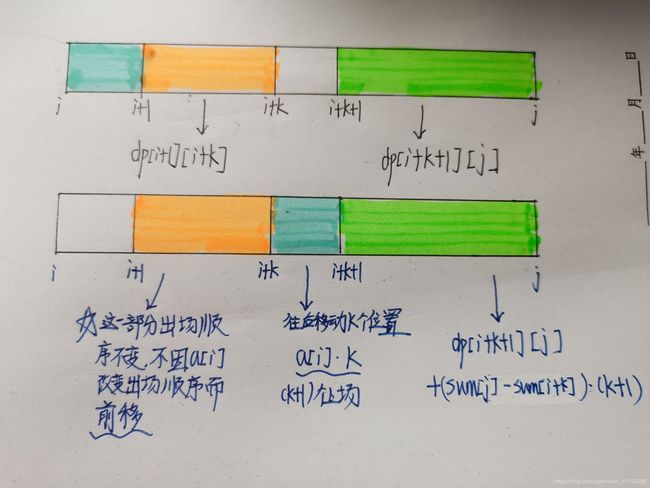
一个区间内的人员调换（如下表）
还是有个点还是没想通，a[i]被放到后面出场，那么dp[i+1,i+k]必然会先出场，那么他们的紧张值为什么没有因为提前一位出场而变化！??
我最后归结为，这一部分dp[i+1,i+k]的出场顺序不变。因为如果他们提前了一位，那么dp[i+k+1,j]便没有后移。

A题收获：
虽然老师给了一套固定模板，我也以为找到状态方程往里套就行。但实际并非如此，虽然都是一个套路，但也要思考后把模板变化着用。
题意：题目很长，理解还是有点难度。共n场晚会，每场晚会都要穿对应的服饰，可以穿多件衣服，脱下的衣服不能再穿，最少需要多少件衣服。
我的思路：1.直接套用课上固定模板。2.不难发现，就两种情况，身上有这件衣服，脱下外面衣服来满足当前晚会；或者就去穿一件新衣服。两者比较取最小。
区间dp[i][j]的含义不再变化，就是区间两个端点，相较经典DP少了变化。
问题点：
1.由于每天的晚会顺序固定，区间不能跳过天数枚举，模板无法套用，要自己思考如何改。

B题收获：
1.课上例题，理解起来也不困难。就是不断枚举区间长度，在去看每个区间的具体情况，但每次看到分隔点k，在区间内起到不断分隔区间，比较各种情况，都觉得非常巧妙。另外就是对下标临界点的考虑。
2.由于每个括号不能组成一对，所以初始化为0。这是和A题不同之处。

C题收获：
我的思路：会发现如果按照题目里的例子思考，会有一个问题：被拿走的牌肯定要删去，但不知道怎么处理。便转换思维：保持首尾两张牌不变，向其中加牌。（模板并不适用）
1.n张牌分解成子区间后，首尾的牌在不断变化。
2.初始化：当区间长度小于3时，值都为0。

石子合并问题---->>>收获：
1.当石子都在一条直线上时，正常处理。
注：
若求石子合并最小得分：将dp[i][j]都初始化为无穷大；
若求石子合并的最大得分，将dp[i][j]都初始化为0。
（ dp[i][i]要初始化为0，因为区间是一个点，无法合并）

2.当石子堆数组成一个圆，收尾相连，处理方式---- >>>由于合并石子的起点无法确定，每堆石子都有可能是起点，所以要将圆转化为1条直线，使得a[i+n]=a[i],扩大一倍石子堆数，但取的区间长度仍为n。相当于对第一种情况的n次起点不同的合并。
注：
1.长度为n的区间有n个，所以要进行循环比较来求得最值。不同于一体直线上的dp[1][n],要对dp[i][i+n-1]循环。
2.相关数组记得开成2*n。对于分隔区间的那层循环（第三层），端点要考虑清楚，几种表示形式都可以。

关于回文字符串的区间DP—收获：
1.将字符串改为回文字符串，可以删除字符或添加字符（代价不同），求出最小代价。
我的思路：挺好想的，如果端点字符相等，则不需要处理；若不相等，比较处理首字符代价和尾字符代价。不相等时转移方程：

dp[i][j]=min(dp[i+1][j]+cost[s[i]-'a'+1],dp[i][j-1]+cost[s[j]-'a'+1])

注：一点开始没想通，删除字符或添加字符虽然代价不同取最小，但是两种不同操作会影响后面的状态---->>>还是没真正理解DP概念，只要确定子问题的规模和原问题是一样的，那么只需要关注子问题即可。

2.从一个字符串中取任意字符构成回文，最多有多少种取法。
我的思路：先从长度为2的区间进行分析，两个字符若相等有3种取法；若长度为3，比如形式为“a b a”，取法应该是3+1+1，3个字符单独构成一个回文，b和两个a构成一个回文，两端a单独构成1个回文。其实到这一步状态方程也差不多该写出来了，但还是差一点，忽略了有些回文被重复计数。
容斥定理：简单来说，就是在两个区间内可能会取到规模一样的字符串，导致重复计数。统计时先算进来，然后再减掉。

dp[i][j]=dp[i][j-1]+dp[i+1][j]-dp[i+1][j-1]

如果首尾字符相等的话，由三部分组成：
dp[i][j]本身的值+dp[i+1][j-1] (区间内任意一个都可和首尾组成新回文）+1（首尾组成）

3.两个兔子一个从顺时针跳，一个逆时针跳，要求跳的石头重量相等，且跳过的不能再跳，问最多进行多少回合。
这题没什么想法，看出好像和回文有关，之后才知道是要找回文非连续序列，而根据回文非连续序列性质，顺时针和逆时针走对于一个区间是一样的。
1.又因为两个兔子只能碰一次面，也就是最终聚集到同一处。---->>>也就转化为求一个区间的最长回文非连续序列。
2.由于每个石头都可能被兔子标记，当作起点，初始化为1。
3.起点不确定，但两只兔子所走的路程是一样的（因为要满足回文），到最后相遇，回合数就等于dp[1][i]+dp[i+1][n]

L题收获：
对于思路，老师上课讲过。几个注意点
1.定义const int inf为极大值时可用memset(dp,-inf,sizeof(dp));将初始化为负无穷。
2.区间内数全部取得的情况要拿出来和区间dp[i][j]前半区间、后半区间进行比较.
3.一个思维点，根据数学公式2*A-sum的值最大，消元思想。

K题收获：
我的思路：本题错误的将dp[i][j]的含义定为区间的两个端点，虽然不停变化对m的讨论，保证最后一分钟的疲劳度为0，但没有办法控制中间的状态，始终想不明白。
看完题解，才发现犯了惯性错误：虽然大多数题目i，j表示的是一个区间，但本题并不是，方向上就错了。
1.dp[i][j]表示第i分钟的j疲劳值（j<=k).
2.两种状态，疲劳度为0时，可以选择在第i分钟跑步，则累加距离；若选择休息，则等于上一分钟的距离。
3.比较疲劳度降到0之前，走的最大距离。感觉这段代码比较难想，我一直想不到怎么处理，非常巧妙，一个倒推思想，所以放上去。

for(int k=0;i<=m;k++)
{
        if(i-k>=0)
    dp[i][0]=max(dp[i][0],dp[i-k][k]
}

博弈补充：
反尼姆博弈：相对于尼姆博弈，最后取得石子的人输！！
结论：先手必胜的情况。
1.所有堆的石子数都为1，且游戏的SG值为0（也就是偶数）。
2.有些堆的石子数大于1且游戏的SG值不为0。（SG的值为所有数的异或结果）

赛后补题
1 Bogosort
将给定数组逆序排列，元素值大的减去小下标肯定大于元素小的减去大下标。满足题意。（过）

2. Adding Powers
队伍当时没做出来的一题。能理解题意：将0加上k的i次方等于给定的数（i只能用一次），且可以是k的不同i次方相加等于给定的数。
这是之前我们没涉及的题目，我们的想法只是简单的枚举，要用到DP记录，感觉上就行不通。
正解：非常巧妙。将给定的数转化为k进制，用数组不断记录输入数对k的取模的值，（进制转换方式）若用到次数>=2，则输出“NO”。

3. Digit Game
被一个简单的思维题卡住了，真的是自己把问题想复杂了。
思路：A对奇数位置上的牌处理，B对偶数位置上的牌进行处理，最后一张牌为奇数，A赢；否则B赢。---->>>我竟然很天真的去统计奇数位置上偶数牌，偶数位置上奇数牌出现次数，傻傻分不清…
实际只需要看奇数位置上是否需要奇数牌，偶数位置上是否出现偶数牌；然后判断总共牌数即可
注：奇数最后一轮到A，先对A判；偶数组后一轮到B，先对B判。代码看似一样，但含义不一样。

4.Air Conditioner
很多有价值的想法无法精炼的总结出来。本质就是不断模拟温度升降过程：温度的该变量就是前后两位客人的差额，如果温度变化的最大值小于客人最低承受温度或最小值大于客人最高承受温度，都无法满足他，直接输出no。

5.The Number of Products
本题两种解法。一种当思维题来做，另一种则是当经典DP来做，算是DP中简单的那种（类似牛吃药跳高那题）。倾向第二种方法：
1.如果数为正数，那么对于负数的方案数不影响，对于正数的方案数+1（需要一个变量不停地对更新的边界方案数累加，“1”代表自己本身为正数便可构成一个方案）
2.如果数为负数，那么正数的方案数为上一个边界负数的方案数（只是起到调整符号的作用），负数的方案数为上一个边界正数的方案数+1.（本身为负数，所以加1，画图！）

---

----我会不会坚持？我会不会坚持？
----做好自己，送走月亮。