《《《翻译》》》三维目标检测

原文名称：Three-Dimensional Object Detection and Layout Prediction using Clouds of Oriented Gradients

原文链接：https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/Ren_Three-Dimensional_Object_Detection_CVPR_2016_paper.pdf

摘要
我们开发了新的表示和算法，用于在杂乱的室内场景中三维物体检测和空间布局预测。传统上，RGB-D图像是通过三维点云的局部几何特征来描述的。我们提出了一个面向梯度的云（COG）描述符，它把物体类别的2D外观和3D姿态联系起来，从而精确地模拟透视投影如何影响感知的图像边界。我们还提出了一种“曼哈顿体素”表示，它更好地捕捉了普通室内环境的3D房间布局几何。有效的分类规则是通过一个结构化的预测框架来学习的，该框架能够解释假设的3D长方体与人类注释的交叉-重叠，以及方位估计误差。类别和布局之间的上下文关系通过级联的分类器捕获，导致整体场景假说具有改进的准确性。
我们的模型仅从带注释的RGB-D图像中学习，没有CAD模型的好处，但是它的性能大大超过SUN RGB-D数据库上的最新水平。避免CAD模型允许更容易地学习许多对象类别的检测器。
1。介绍
过去十年中，用于2D图像的语义理解的算法取得了重大进展[6，29]。室内（家庭或办公室）环境的图像，通常高度杂乱，并具有实质性的遮挡，对现有的模型特别具有挑战性。深度传感器技术的最新进展大大降低了标准RGB图像中存在的模糊性，使得场景布局预测[22、13、41]、支持表面预测[34、8、10]、语义解析[11]和对象检测[36]得以突破。为了训练和评价室内场景理解方法，已经构建了越来越多的带注释的RGB-D数据集[30、21、34、35]。
已经开发了广泛的语义3D场景模型，包括基于低级体素表示的方法[20]。概括广泛用于2D检测的边界框，对象实例的3D大小、位置和方向可以通过边界长方体（凸多面体）来描述。几种方法将长方体模型拟合到RGB或RGB-D数据[17、16、40]，但是没有任何语义的、高层次的场景理解。其他工作已经使用CRF对通过自底向上分组[25]检测到的长方体进行分类，或通过与“滑动”位置中的已知CAD模型匹配[36]在3D中直接检测到对象。
最近几篇论文已经使用CAD模型作为用于室内场景理解的附加信息，通过学习对象形状[39]的模型或基于外观匹配的幻觉替代视点[1,24,23]。因此这些方法通常只关注少数类别（通常，只是椅子[1]）。此外，基于示例的方法[36]可能由于需要将每个示例与每个测试图像匹配而计算效率低下。不清楚需要多少CAD模型才能忠实地捕获对象类。
为了对室内场景的空间布局进行建模，许多方法都采用正交的“曼哈顿”结构[4]，并且目的在于推断3D结构的2D投影。在[22]和[15]的基础上，Hedau等人。[12]使用结构化模型来重新排列布局假设，Schwing等。_33_提出了一种有效的积分表示法，以有效地探索成指数分布的许多布局建议，以及Zhang等。[41]合并深度线索。联合建模对象可以提高布局预测精度[13，32]，但是以前的工作集中在受限的环境（例如，几乎总是与墙壁对齐的床）上，并且可能不能概括为更杂乱的场景。其他工作已经使用点云数据直接预测3D布局[25，35]，但是对RGB-D深度估计中的误差敏感。
简单的场景解析算法可以独立地检测每个类别，即使在非最大值抑制后也会引入许多误报。以前的工作已经使用相当精细的、人工设计的启发式来修剪错误检测[36]，或者联合使用CAD模型和布局线索来建模场景[9]。在本文中，我们展示了一个级联的分类框架[14]可以用来学习对象类别和总体房间布局之间的上下文关系，从而视觉上独特的对象导致更高质量的整体场景解释。

我们提出了一个只使用RGB-D注释学习多个对象类别的检测器的通用框架。在第2节、引入一种新的面向梯度云（COG）特征，将三维物体姿态与二维图像边界牢固地联系起来。我们还引入了一种新的曼哈顿体素表示三维房间布局几何。然后，我们使用结构化预测框架（Sec.3)学习将3D长方体假设与RGB-D数据对齐的算法和级联分类器(Sec.4)合并来自其他对象实例和类别的上下文线索以及整个3D布局。在第5节 我们使用最近引入的大型SUN-RGBD数据集[35]来验证我们的方法，其中我们以比最先进的CAD模型检测器更高的精度检测更多的类别[36]。
2。三维几何及外观建模
我们的对象检测器是从SUN-RGBD数据集[35]中面向3D的长方体注释中学习的，其中包含10335个RGB-D图像和19个标记的对象类别。我们将每个长方体离散成6×6×6的(大)体素网格，并提取这些63=216个单元的特征。体素维度被缩放以匹配每个实例的大小。我们使用标准描述符描述观测深度图像的三维几何，并提出了一种新的RGB外观的朝向梯度云（COG）描述符。我们提出了曼哈顿三维空间布局几何体素模型。
2.1。物体几何学：三维密度和方向
点云密度以3D长方体注释或检测假设为条件，假设体素“包含Ni”点。我们使用透视投影来寻找图像中每个体素的轮廓，并计算凸区域的面积Ai。体素`然后等于φa i`=Ni`/Ai'的点云密度特征。归一化对场景中物体的深度变化具有鲁棒性。我们通过局部体素区域进行归一化，而不是像某些相关工作[36]中那样通过长方体中点的总数进行归一化，以对部分对象遮挡提供更强的鲁棒性。
对于垂直于3D表面的矢量，已经提出了各种表示，例如自旋图像[19]。与[36]中一样，我们在每个体素内建立法线方向的25元直方图，并且通过拟合其15个最近邻的平面来估计每个3D点的法线方向。这个特征φb i通过局部3D方向的图案捕获长方体i的表面形状。
2.2。定向梯度云
定向梯度直方图（HOG）描述符[5]是许多有效目标检测方法的基础[6]。由于普通物体产生的强遮挡轮廓，边缘是室内场景理解的一个非常自然的基础。然而，梯度方向当然是由三维物体方向和透视投影确定的，所以在2D图像坐标中天真地提取的HOG描述符普遍性较差。为了解决这个问题，以前的一些工作已经使用3DCAD模型来幻觉边缘，这些边缘从各种合成观点来看都是可以预期的[23，1]。其他工作限制性地假设物体的部分是非平面的，以便图像扭曲可用于对齐[7]，或者所有物体具有与房间[13]的全球“曼哈顿世界坐标”对齐的3D姿态。HOG描述符[3,31]的一些先前的3D扩展假定给出了完整的3D模型或网格模型。在最近的独立研究[37]中，3D长方体假设被用于从深度卷积神经网络中聚集标准2D特征，但是这些特征和3D对象定向之间的关系没有建模。我们的定向梯度云（COG）特征精确地描述了具有复杂3D几何形状的物体的3D外观，如RGBD摄像机以任何方向捕捉到的。

梯度计算 我们通过将滤波器[1，0，1]，[1，0，1]T应用到未平滑的2D图像的RGB通道来计算梯度。跨颜色通道的最大响应是x和y方向上的梯度（dx，dy），具有相应的幅度pdx2+dy2。
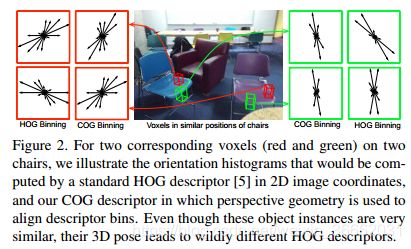
三维定位仓 标准HOG描述符[5]使用均匀间隔的梯度箱，其中0_是水平图像方向。如图2所示，这会为处于不同姿态的对象产生非常不一致的描述符。
对于每个长方体，我们构造了九个三维定向箱，这些定向箱与沿水平轴垂直放置的半圆盘中的0_180_均匀间隔。然后，我们使用透视投影来找到相应的2D边框。对于位于给定3D体素内的每个点，我们将其无符号2D梯度累积在相应的投影2D定向框中。为了避免对具有非平面几何形状的物体不稳定的图像处理操作，我们使用弯曲直方图盒来累积标准梯度，而不是通过扭曲图像来匹配固定方向盒。
归一化和混叠 我们双线性地插值相邻方向盒之间的梯度大小[5]。为了标准化长方体i中体素的直方图φc i`i'，我们然后将

设置为系数大于0。考虑到所有的方位和体素，COG特征的维数为63×9=1944。

2.3。房间布局几何学：曼哈顿体素
给定RGB-D图像，场景解析不仅需要对象检测，还需要房间布局（地板、天花板、墙壁）预测[12、22、41、32]。这种“自由空间”的理解对于机器人导航等应用至关重要。以前很多方法把房间布局预测看成是2D标注任务[2,33,41]，但是2D中的小错误会导致3D布局预测中的巨大误差。简单的RGB-D布局预测方法[35]通过将平面拟合到观测点云数据来工作。我们提出了一个更精确的基于学习的方法来预测曼哈顿几何。
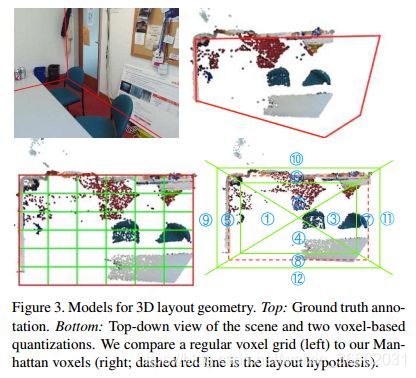
标准房间的正交墙可以通过长方体[27]表示，我们可以通过标准体素离散化定义几何特征（图3，左下）。然而，因为角体素通常包含两个壁的交集，所以它们然后混合具有非常不同方向的3D法向量。此外，这种离散化忽略了假设长方体之外的点，并且可以匹配具有壁状结构的房间的子集。
我们提出一个新的曼哈顿体素（图3，右下角）离散化三维布局预测。我们首先把地板和天花板之间的垂直空间离散成6个相等的箱子。然后，我们使用0.15m的阈值将墙壁附近的点和虚拟布局的内部和外部的点分开。进一步使用对角线在房间角落处分割箱子，整个空间被离散为12×6=72个箱子。对于每个垂直层，区域R1：4模拟场景内部，其点云分布在图像之间变化很大。区域R5：8模型点靠近假定的曼哈顿墙结构：R5和R6应该包含正交的平面，而R5和R7应该包含平行的平面。区域R9:12捕捉在预测布局之外的点，这可能是由透明表面上的深度传感器误差产生的。

3。学习检测长方体和布局
对于训练图像Ii中标注的一些长方体Bi中的每个体素，我们有一点云密度特征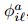、25个表面法向直方图特征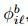和9个COG外观特征。我们基于特征的长方体i的整体表示是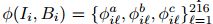。利用SUN-RGBD数据集[35]中提供的重力方向，通过如图1所示的带注释的方位对准长方体。类似地，对于布局假设Mi中的每个曼哈顿体素，我们计算点云密度和表面法线特征，以及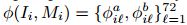

3.1.物体立方体的结构预测
对于每个对象类别c，使用包含该类别的可见实例的图像，我们的目标是学习预测函数hc：I_B，该函数将RGB-D图像I映射到3D边界框B=(L，θ，S)。
这里，L是长方体的三维中心，θ是长方体的方向，S是长方体沿其方向确定的三个轴的物理尺寸。我们假设物体有一个通常支撑它们的基座，因此θ是相对于地面的标量旋转。
给定类别c的训练示例，我们使用具有边际重标度约束的结构支持向量机(SVM)目标[18]的ns.公式：

这里，φ(Ii，Bi)是定向长方体假设的特征Bi给定RGB-D图像Ii，Bi是基本真值注释边界框，Bi是可能的替代边界框集合。对于具有多个实例的训练图像，如同之前关于2D检测的工作[38]一样，我们多次将图像添加到训练集中，每次都删除其他实例中包含的3D点的子集。
给定一些基真长方体B和估计长方体B，我们定义以下损失函数：

这里，IOU(B，B)是长方体的3D相交的体积，除以它们的3D结合的体积。当IOU(B，B-)接近1且方位误差θ-θ-=0时，损耗最小。如果位置或方向错误，损失接近1。我们用截平面法求解方程（1）的损耗敏感目标[18]。我们还用基于标准二进制SVM的具有硬负挖掘的检测器进行了实验，但是发现损失敏感的S-SVM分类器更精确（参见图5），并且在处理大量负长方体假设方面也更有效。

长方体假设我们用离散的3D世界坐标以滑动窗口的方式预计算候选长方体的特征，具有16个候选方向。我们使用训练边界框的经验统计量来离散长方体大小：{0.1，0.3，0.5，0.7，0.9}宽度分位数，{0.25，0.5，0.75}深度分位数和{0.3，0.5，0.8}高度分位数。然后评估体素大小、3D位置和方向的每个组合。
3.2。曼哈顿布局的结构化预测
我们再次使用方程（1）的S-SVM公式来预测曼哈顿布局长方体M=（L，θ，S）。损耗函数(M，M)与等式(2)相同，只是我们使用[35]中IOU的“自由空间”定义，并且说明方向仅是可识别的模90_旋转。因为布局注释不一定具有曼哈顿结构，所以地面真值布局被认为是具有最大自由空间IOU的长方体假设。
布局假设我们预测楼层和天花板为沿重力方向的三维点的0.001和0.999分位数，并将方向离散成0_和180之间的18个均匀间隔角。然后，我们提出布局候选，它捕获所有3D点的至少80%，并且由最远和最近的3D点界定。对于典型的场景，有5000-20000个布局假设。有关更多细节，请参阅补充材料。
4。空间语境的级联学习
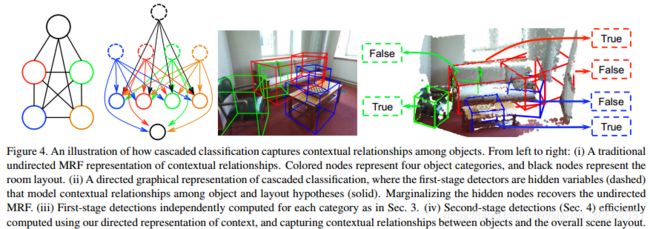
如果探测器是在Sec.3是针对每个类别独立应用的，可能存在许多误报，其中大对象的“块”被检测为较小对象（参见图4）。宋等。[36]通过启发式降低对于大图像段上的小检测的置信度得分来减少这种误差。为了避免这种必须经常调整到每个类别的手动工程，我们建议直接学习不同类别的检测之间的关系。由于房间几何形状也是物体检测的重要线索，我们结合曼哈顿布局假说来理解整个场景[35，25]。通常，空间关系的结构化预测是通过无向马尔可夫随机场（MRF）[26]实现的。如图4所示，这通常导致完全连通的图[28]，因为每对对象类别之间存在关系。一个极具挑战性的MAP估计（或能量最小化）问题必须在每次训练迭代以及针对每个测试图像解决，因此学习和预测是昂贵的。
我们建议将级联分类[14]用于3D场景中上下文关系的建模。在这种方法中，“第一阶段”检测如在Sec.3成为“第二阶段”分类器的输入特征，该分类器估计对长方体假设正确性的置信度。

这可以解释为具有隐藏变量的有向图形模型。对第一阶段变量进行边际化可以恢复标准的、完全连接的无向图。然而，至关重要的是，级联表示效率更高：训练分解为每个节点（对象类别）的独立学习问题，并且通过快速局部决策序列可以实现最优测试分类。
对于一对重叠的检测边界框Bi和Bj，我们表示它们的体积为V(Bi)和V(Bj)，它们的重叠体积为O(Bi，Bj)，它们的结合体积为U(Bi，Bj)。我们通过三个特征来表征它们的几何关系：

为了建立物体布局上下文[25]的模型，我们计算了长方体Bi到布局M中最近壁的距离D(Bi，M)和角度A(Bi，M)。

第一级检测器为每个类别提供最可能的布局假设以及一组检测（在非最大抑制之后）。对于具有置信度得分zi的边界框Bi，可能存在若干类别c∈{1，.…，C}。设i c为具有最大置信度zi c的类别fai i的实例，通过zi的二次函数、S1:3(i，i c)、A(Bi，M)和D(Bi，M)的径向基展开式来创建边界框Bi的特征i。第二阶段布局候选对象和对象长方体之间的关系被类似地建模。有关详细信息，请参阅补充材料。
由于级联的有向图形结构，每个第二级检测器可以独立地学习。目的是简单的二进制分类：候选检测是真阳性还是假阳性？在训练期间，如果每个类对地面真值实例的交-合得分大于0.25，则每个检测到的类的边界框被标记为“true”，并且是这些检测中最大的。我们训练一个具有径向基函数（RBF）核的标准二进制SVM。

使用验证数据选择带宽参数γ。虽然我们使用RBF核用于所有报告的实验，线性SVM的性能只是稍微差一点，并且级联分类仍然为更可伸缩的训练目标提供有用的性能增益。
为了训练第二阶段布局预测器（图4中的底部节点），我们将对象布局特征与来自Sec.2.3，再次利用S-SVM训练对自由空间IOU进行优化。在测试期间，给定在第一阶段滑动窗口搜索中发现的一组长方体，我们将第二阶段级联分类器应用于每个长方体Bi，以获得新的上下文置信分数zi0。然后，用于精确回忆评估的总置信度得分为zi+zi0，以说明几何和COG特征的原始信念以及上下文线索的校正能力。第二阶段布局预测由第二阶段S-SVM分类器直接提供。
5。实验
我们在SUN RGB-D数据集[35]上测试了我们的级联模型，并与最先进的滑动形状[36]长方体探测器和[35]中的基线布局预测器进行了比较。旧的NYU深度数据集[34]是SUN RGB-D的子集，但是SUN RGB-D改进了注释和许多新图像。由于与先前的工作不同，我们不使用CAD模型，因此我们很容易学习和评估10种对象类别的RGBD外观模型，其中5种多于[36]。对象长方体和3D布局假设的生成和评估，如前几节所述。
我们使用交点合并和基本真值长方体注释来评估检测性能，并且当分数高于0.25时，我们认为预测框是正确的。为了评估布局预测性能，我们使用人工注释计算自由空间交集。我们提供了几个比较来证明我们的场景理解系统的有效性，以及外观和上下文特征的重要性。

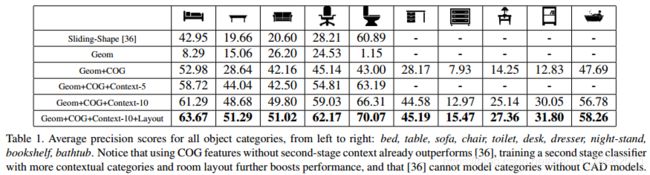
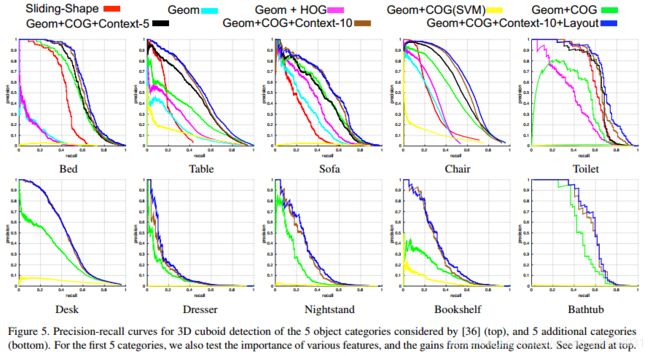
我们仅用几何特征（Geom）和添加COG特征（Geom+COG）来训练检测器。对于所有对象类别的检测精度都有非常明显的提高（参见表1和图5中的精度-召回曲线）。仅基于噪声点云的目标检测器是不完善的，并且RGB图像包含互补信息。
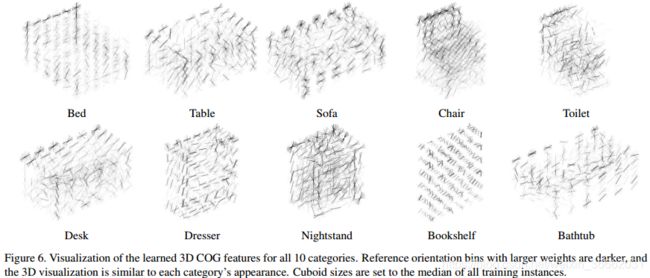
HOG与COG 为了验证COG特征的有效性，我们还使用Na_ve2D桶提取每个3D长方体的HOG特征，并训练检测器(Geom+HOG)。由于固定的2D桶不与3D物体姿态的变化对齐，因此该特征的信息量较少，并且检测性能比使用校正后的COG桶进行透视投影时差得多。我们将学习到的COG特征可视化到图6的不同类别中。我们可以看到许多描述性的外观提示，例如每个对象的定向外部边界，以及沙发、椅子、厕所和浴缸的空心区域。
立体体素与曼哈顿体素 我们使用自由空间IOU[35]来评估布局预测算法的性能。使用标准立方体体素，我们的性能（72.33）与启发式SUN RGB-D基线（73.4，[35]）类似。结合曼哈顿体素和结构化学习，性能提高到78.96，证明了这种改进的离散化的有效性。此外，如果我们还结合了来自检测对象的上下文线索，则得分提高到80.23。我们在图7中提供了一些布局预测示例。
语境的重要性 为了证明级联分类器有助于修剪假阳性，我们使用来自第一级分类器的置信度得分以及来自第二级分类器的更新置信度得分(Geom+COG+Context-5)来评估检测。如表1和图5所示，添加上下文级联明显提高了性能。此外，当建模更多的对象类别（Geom+COG+Context-10）时，性能将进一步提高。这个结果证明，即使少量的对象是主要的兴趣，建立更广泛的场景的模型可以是非常有益的。
我们在图8中显示了一些有代表性的检测结果。在第一幅图像中，我们的椅子检测器被弄混了，沙发上起了火，但是在其他检测到的边框的上下文提示的帮助下，这些假阳性被去除了。对于跨越所有对象类别的固定阈值，我们有与滑动形状基线一样多的真实检测，同时产生较少的假阳性。
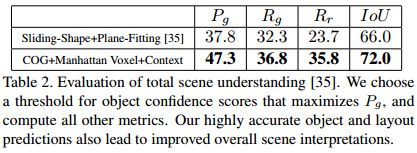
全景理解 通过捕获对象对之间的上下文关系，以及对象与整个3D房间布局之间的关系，我们的级联分类器使我们能够执行总体场景理解的任务[35]。我们通过对所有第二阶段对象建议应用相同的阈值（根据验证数据调整）来生成单个全局场景假设，并选择最高得分的布局预测。我们报告由表2中的[35]定义的精度、召回和IOU评估度量。在每种情况下，我们显示出比基线明显的改进。
计算速度该算法在MATLAB中实现，大部分运行时间用于特征计算。对于典型的室内图像，我们的算法将花费10到30分钟来计算一个对象类别的特征和曼哈顿体素离散化，以及2秒来预测3D长方体和布局假设。这种速度可以以各种方式显著提高，例如利用积分图像进行特征计算[36]或使用GPU硬件进行并行化。
6。结论
提出了一种基于RGB-D图像的三维长方体检测和曼哈顿房间布局预测算法。使用我们新颖的3D外观COG描述符，我们训练了针对10个对象类别的精确的3D长方体检测器，以及学习上下文线索以修剪假阳性的级联分类器。我们的场景表示直接从RGB-D数据中学习，没有外部CAD模型，并且可以推广到许多其他类别。
这项研究部分得到了ONR奖编号N00014-13-1-0644的支持。

References
[1] M. Aubry, D. Maturana, A. Efros, B. Russell, and J. Sivic.Seeing 3D chairs: Exemplar part-based 2D-3D alignment using a large dataset of CAD models. In CVPR, 2014.
[2] J. Bai, Q. Song, O. Veksler, and X. Wu. Fast dynamic programming for labeling problems with ordering constraints.In CVPR, pages 1728–1735. IEEE, 2012.
[3] N. Buch, J. Orwell, and S. A. Velastin. 3D extended histogram of oriented gradients (3dhog) for classification of road users in urban scenes. In BMVC, 2009.
[4] J. M. Coughlan and A. L. Yuille. Manhattan world: Compass direction from a single image by Bayesian inference. In ICCV, volume 2, pages 941–947. IEEE, 1999.
[5] N. Dalal and B. Triggs. Histograms of oriented gradients for human detection. In CVPR, volume 1, pages 886–893. IEEE, 2005.
[6] M. Everingham, L. Van Gool, C. K. I. Williams, J. Winn, and A. Zisserman. The PASCAL Visual Object Classes Challenge 2012 (VOC2012) Results.
[7] S. Fidler, S. Dickinson, and R. Urtasun. 3D object detection and viewpoint estimation with a deformable 3D cuboid model. In NIPS, pages 611–619, 2012.
[8] D. F. Fouhey, A. Gupta, and M. Hebert. Unfolding an indoor origami world. In ECCV, pages 687–702. Springer, 2014.
[9] A. Geiger and C. Wang. Joint 3D object and layout inference from a single RGB-D image. In German Conference on Pattern Recognition (GCPR), 2015.
[10] R. Guo and D. Hoiem. Support surface prediction in indoor scenes. In ICCV, pages 2144–2151. IEEE, 2013.
[11] S. Gupta, R. Girshick, P. Arbelaez, and J. Malik. Learning ´ rich features from RGB-D images for object detection and segmentation. In ECCV, pages 345–360. Springer, 2014.
[12] V. Hedau, D. Hoiem, and D. Forsyth. Recovering the spatial layout of cluttered rooms. In CVPR, pages 1849–1856. IEEE, 2009.
[13] V. Hedau, D. Hoiem, and D. Forsyth. Thinking inside the box: Using appearance models and context based on room geometry. In ECCV, pages 224–237. Springer, 2010.
[14] G. Heitz, S. Gould, A. Saxena, and D. Koller. Cascaded classification models: Combining models for holistic scene understanding. In NIPS, pages 641–648, 2009.
[15] D. Hoiem, A. Efros, M. Hebert, et al. Geometric context from a single image. In CVPR, volume 1, pages 654–661. IEEE, 2005.
[16] Z. Jia, A. Gallagher, A. Saxena, and T. Chen. 3D-based reasoning with blocks, support, and stability. In CVPR, pages 1–8. IEEE, 2013.
[17] H. Jiang and J. Xiao. A linear approach to matching cuboids in RGBD images. In CVPR, 2013.
[18] T. Joachims, T. Finley, and C.-N. J. Yu. Cutting-plane training of structural SVMs. Machine Learning, 77(1):27–59, 2009.
[19] A. E. Johnson and M. Hebert. Using spin images for efficient object recognition in cluttered 3D scenes. PAMI, 21(5):433– 449, 1999.
[20] B.-s. Kim, P. K. Kohli, and S. Savarese. 3D scene understanding by voxel-CRF. In ICCV, 2013.
[21] K. Lai, L. Bo, X. Ren, and D. Fox. A large-scale hierarchical multi-view RGB-D object dataset. In ICRA, pages 1817– 1824. IEEE, 2011.
[22] D. C. Lee, M. Hebert, and T. Kanade. Geometric reasoning for single image structure recovery. In CVPR, pages 2136– 2143. IEEE, 2009.
[23] J. J. Lim, A. Khosla, and A. Torralba. FPM: Fine pose partsbased model with 3D CAD models. In ECCV, pages 478– 493. Springer, 2014.
[24] J. J. Lim, H. Pirsiavash, and A. Torralba. Parsing IKEA objects: Fine pose estimation. In ICCV, 2013.
[25] D. Lin, S. Fidler, and R. Urtasun. Holistic scene understanding for 3D object detection with RGBD cameras. In ICCV, pages 1417–1424. IEEE, 2013.
[26] S. Nowozin and C. H. Lampert. Structured learning and prediction in computer vision. Foundations and Trends in Computer Graphics and Vision, 6(3–4):185–365, 2011.
[27] L. D. Pero, J. Guan, E. Brau, J. Schlecht, and K. Barnard. Sampling bedrooms. In CVPR, pages 2009–2016. IEEE, 2011.
[28] A. Rabinovich, A. Vedaldi, C. Galleguillos, E. Wiewiora, and S. Belongie. Objects in context. In ICCV, 2007. 
[29] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg, and L. Fei-Fei. ImageNet Large Scale Visual  Recognition Challenge. IJCV, 2015.
[30] B. C. Russell and A. Torralba. Building a database of 3D scenes from user annotations. In CVPR, pages 2711–2718. IEEE, 2009.
[31] M. Scherer, M. Walter, and T. Schreck. Histograms of oriented gradients for 3D object retrieval. In Europe on Computer Graphics, Visualization and Computer Vision, 2010.
[32] A. G. Schwing, S. Fidler, M. Pollefeys, and R. Urtasun. Box in the box: Joint 3D layout and object reasoning from single images. In ICCV, pages 353–360. IEEE, 2013.
[33] A. G. Schwing, T. Hazan, M. Pollefeys, and R. Urtasun. Efficient structured prediction for 3D indoor scene understanding. In CVPR, pages 2815–2822. IEEE, 2012.
[34] N. Silberman, D. Hoiem, P. Kohli, and R. Fergus. Indoor segmentation and support inference from RGBD images. In ECCV, pages 746–760. Springer, 2012.
[35] S. Song, L. Samuel, and J. Xiao. SUN RGB-D: A RGB-D scene understanding benchmark suite. In CVPR. IEEE, 2015.
[36] S. Song and J. Xiao. Sliding shapes for 3D object detection in depth images. In ECCV, pages 634–651. Springer, 2014.
[37] S. Song and J. Xiao. Deep sliding shapes for amodal 3D object detection in RGB-D images. In CVPR, 2016.
[38] A. Vedaldi and A. Zisserman. Structured output regression for detection with partial occulsion. In NIPS, 2009.
[39] Z. Wu, S. Song, A. Khosla, X. Tang, and J. Xiao. 3D shapenets for 2.5D object recognition and next-best-view prediction. arXiv preprint arXiv:1406.5670, 2014.
[40] J. Xiao, B. C. Russell, and A. Torralba. Localizing 3d cuboids in single-view images. In NIPS, 2012.
[41] J. Zhang, C. Kan, A. G. Schwing, and R. Urtasun. Estimating the 3D layout of indoor scenes and its clutter from depth sensors. In ICCV, pages 1273–1280. IEEE, 2013.