用python实现改遗传算法解柔性作业车间调度问题的编码和初始化

用python实现遗传算法的编码及初始化

柔性车间调度问题描述如下：n个工件（J1,J2,J3...，Jn）要在m台机器（M1,M2....Mm）上加工；每个工件包含一道或多道工序；工序顺序是预先确定的；每道工序可以在多台不同加工机器上进行加工；工序的加工时间随加工机器的不同而不同；调度目标是为每到工序选择最合适的机器，确定每台机器上各道工序最佳加工顺序及开工时间，使整个系统的某些性能指标达到最优。

注：我个人认为初始化以及明晰的编码方式是每个初学者进入智能优化算法学习的敲门砖，因此，本文从次开始，详细讲解编码及初始化方式，帮初入门的同学，能更快的入门。

---

问题描述：改进遗传算法的染色体的编码问题

首先，先大致描述一下遗传算法的过程：

步骤1：按照一定的初始化方法产生初始种群P(t),t=0.

步骤2：评价种群P（t）,计算每个个体的适应度

步骤3:   判断是否满足终止条件，如果满足则输出结果；否则转步骤4

步骤4：按照选择、交叉、变异等遗传算子产生子代

步骤5： P（t）=C(t),转步骤2，t=t+1

---

 

编码

         染色体编码是将所研究的问题的解用染色体的形式来表达的，这是遗传算法的关键。编码的目的是为了实现交叉、变异等类似生物界的遗传操作。

          FJSP包括两个问题：机器选择和工序排序。机器选择解决每道工序在可选机器集中的哪台机器上加工的问题；工序排序解决所有工序确定加工机器后的排序和开工时间问题。针对编码过程中两个问题编码处理的不同，目前主要有以下两种不同的编码方法。

          （1）集成编码：集成编码染色体中的每一个基因位（h,j,i）代表一个工序任务，表示工件j的第h道工序在机器i上加工，染色体总长度等于所有工件的工序总和T0.

          （2）分段编码：分段编码染色体有A/B两部分组成，将工序信息分开处理，分别表示FJSP的两个子问题，两部分染色体长度都等于T0.

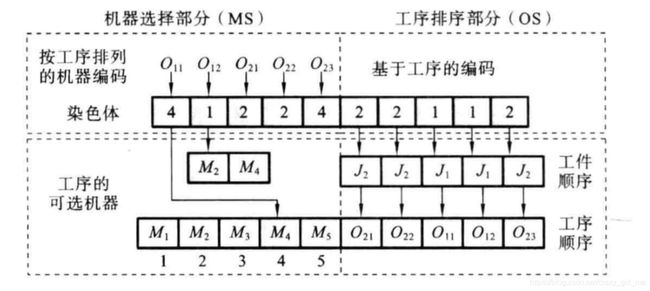
          本文参考高亮的《柔性作业车间调度智能算法及其应用》一书中的编码方法：即整数编码MSOS,由两部分组成：机器部分（machines selection,MS）和工序排序部分（operations sequencing,OS）,如下图

注：机器选择部分：T0=所有工件的工序数的和，每个基因位用整数表示，依次按照工件和工件的工序进行排列，每个整数表示当前工序选择的加工机器在可选机器在可选机器集的顺序编码，并不是对应的机器号。

       工序选择部分：每一个基因用工件号直接编码，工件号出现的顺序表示该工件工序间的先后加工顺序，即对染色体从左到右进行编译，对于第h次出现的工件号，表示该工件j的第h道工序，并且工件号的出现次数等于该工件的工序总数hj

初始化

            种群初始化是进化算法中是一个关键问题，初始解的质量对遗传算法求解的速度和质量有非常大的影响。本文依然参考高亮书中的第三章内容，即初始化方式分为：全局选择（global selection,GS）、局部选择（local selection,LS）和随机选择（random selection,RS）.

1、全局选择：工件为随机从工件集中选择一个工件并且机器时间数组从头到尾都不归零。具体过程如下：

2、局部选择：从工件集的第一个工件开始取，按顺序取出所有工件，机器时间数组每次都要归零

3、随机选择

                                  

---

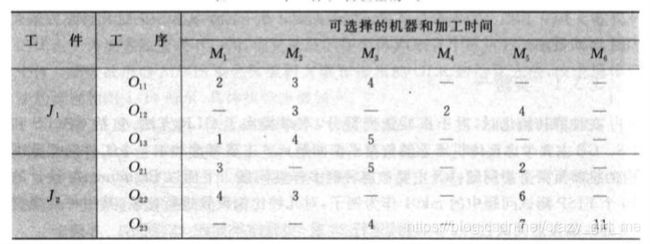
例题：

 

---

代码如下：

 

import numpy as np
import matplotlib.pyplot as plt
import random
import itertools

GSP=0.6             #全局选择的GS概率
LSP=0.3             #局部选择的LS概率
RSP=0.1             #随机选择的RS概率
POP_SIZE=10         #种群规模
Max_Itertions=100   #最大迭代次数=100
T0_1=12             #染色体长度的一半
M0=6                #机器数
N=4                 #工件数
GS_1=int(POP_SIZE*GSP)     #全局选择的个数
LS_1=int(POP_SIZE*LSP)     #局部选择的个数
RS_1=int(POP_SIZE*RSP)     #随机选择的个数

CSH=np.zeros([POP_SIZE,T0_1*2],dtype=int)    #初始化种群
GS_MS_1=CSH[0:GS_1,0:T0_1]                   #机器选择部分MS
GS_OS_1=CSH[0:GS_1,T0_1:2*T0_1]              #工序选择部分OS
LS_MS_1=CSH[0:LS_1,0:T0_1]                   #机器选择部分MS
LS_OS_1=CSH[0:LS_1,T0_1:2*T0_1]              #工序选择部分OS
RS_MS_1=CSH[0:RS_1,0:T0_1]                   #机器选择部分MS
RS_OS_1=CSH[0:RS_1,T0_1:2*T0_1]              #工序选择部分OS

O_set1=[1,2,3,4]

OS_List=[1,1,1,2,2,2,3,3,3,4,4,4]

L=[
    [[2,3,4,9999,9999,9999],[9999,3,9999,2,4,9999],[1,4,5,9999,9999,9999]],     #第一个工件及其对应的机器加工时间
    [[3,9999,5,9999,2,9999],[4,3,9999,9999,6,9999],[9999,9999,4,9999,7,11]],    #第二个工件及其对应的机器加工时间
    [[5,6,9999,9999,9999,9999],[9999,4,9999,3,5,9999],[9999,9999,13,9999,9,12]],#第3个，。。。。
    [[9,9999,7,9,9999,9999],[9999,6,9999,4,9999,5],[1,9999,3,9999,9999,3]],     #第4个，。。。。
]
O_L=np.array(L)
#全局初始化
#机器选择部分
def Global_initial(T0,O,GS,MS,n,M,OS_list,OS):
    for i in range(GS):
        Machine_time = np.zeros(M,dtype=int)          # 机器时间初始化
        random.shuffle(OS_list)  # 生成工序排序部分
        OS[i] = np.array(OS_list)
        GJ_list=[]
        for GJ_Num in range(n):         #工件集
            GJ_list.append(GJ_Num)
        random.shuffle(GJ_list)
        # print(GJ_list)
        for g in GJ_list:    # 随机选择工件集的第一个工件,从工件集中剔除这个工件
            h = np.array(O[g])  # 第一个工件含有的工序
            for j in range(len(h)):  # 从工件的第一个工序开始选择机器
                D = np.array(h[j])
                List_Machine_weizhi = []
                for k in range(len(D)):  # 每道工序可使用的机器以及机器的加工时间
                    Useing_Machine = D[k]
                    if Useing_Machine == 9999:  # 确定可加工该工序的机器
                        continue
                    else:
                        List_Machine_weizhi.append(k)
                Machine_Select = []
                for Machine_add in List_Machine_weizhi:  # 将这道工序的可用机器时间和以前积累的机器时间相加
                    Machine_time[Machine_add] = Machine_time[Machine_add] + D[
                        Machine_add]  # 比较可用机器的时间加上以前累计的机器时间的时间值，并选出时间最小
                    Machine_Select.append(Machine_time[Machine_add])
                Min_time=min(Machine_Select)
                Machine_Index_add = Machine_Select.index(Min_time)
                MS[i][g*3+j] =Machine_Index_add + 1

    CHS1=np.hstack((MS,OS))
    return CHS1
#局部选择

def Local_initial(T0,O,LS,MS,n,M,OS_list,OS):
    for i in range(LS):
        random.shuffle(OS_list)  # 生成工序排序部分
        OS_gongxu = OS_list
        # print(OS_gongxu)
        # print('************************')
        OS[i] = np.array(OS_gongxu)
        GJ_list=[]
        for GJ_Num in range(n):         #工件集
            GJ_list.append(GJ_Num)
        A=0
        for gon in GJ_list:
            Machine_time = np.zeros(M)          # 机器时间初始化
            g = gon                      # 随机选择工件集的第一个工件   #从工件集中剔除这个工件
            h = np.array(O[g])  # 第一个工件及其对应工序的加工时间
            for j in range(len(h)):  # 从工件的第一个工序开始选择机器
                D = np.array(h[j])
                List_Machine_weizhi = []
                for k in range(len(D)):  # 每道工序可使用的机器以及机器的加工时间
                    Useing_Machine = D[k]
                    if Useing_Machine == 9999:  # 确定可加工该工序的机器
                        continue
                    else:
                        List_Machine_weizhi.append(k)
                Machine_Select = []
                for Machine_add in List_Machine_weizhi:  # 将这道工序的可用机器时间和以前积累的机器时间相加
                    Machine_time[Machine_add] = Machine_time[Machine_add] + D[Machine_add]  # 比较可用机器的时间加上以前累计的机器时间的时间值，并选出时间最小
                    Machine_Select.append(Machine_time[Machine_add])
                Machine_Index_add = Machine_Select.index(min(Machine_Select))
                MS[i][g*3+j] = MS[i][g*3+j] + Machine_Index_add + 1
                A+=1
    CHS1=np.hstack((MS,OS))
    return CHS1
#随机选择
def Random_initial(T0,O,RS,MS,n,M,OS_list,OS):
    for i in range(RS):
        random.shuffle(OS_list)  # 生成工序排序部分
        OS_gongxu = OS_list
        OS[i] = np.array(OS_gongxu)
        GJ_list=[]
        for GJ_Num in range(n):         #工件集
            GJ_list.append(GJ_Num)
        A=0
        for gon in GJ_list:
            Machine_time = np.zeros(M)          # 机器时间初始化
            g = gon                      # 随机选择工件集的第一个工件   #从工件集中剔除这个工件
            h = np.array(O[g])  # 第一个工件及其对应工序的加工时间
            for j in range(len(h)):  # 从工件的第一个工序开始选择机器
                D = np.array(h[j])
                List_Machine_weizhi = []
                for k in range(len(D)):  # 每道工序可使用的机器以及机器的加工时间
                    Useing_Machine = D[k]
                    if Useing_Machine == 9999:  # 确定可加工该工序的机器
                        continue
                    else:
                        List_Machine_weizhi.append(k)
                Machine_Select = []
                for Machine_add in List_Machine_weizhi:  # 将这道工序的可用机器时间和以前积累的机器时间相加
                    Machine_time[Machine_add] = Machine_time[Machine_add] + D[
                        Machine_add]  # 比较可用机器的时间加上以前累计的机器时间的时间值，并选出时间最小
                    Machine_Select.append(Machine_time[Machine_add])
                Machine_Index_add = Machine_Select.index(random.choice(Machine_Select))

                MS[i][A] = MS[i][A] + Machine_Index_add + 1
                A+=1
    CHS1=np.hstack((MS,OS))
    return CHS1

这个编码很多小伙伴反应有一些错误，所以采用了改良版本的：

改良版本链接： https://blog.csdn.net/crazy_girl_me/article/details/114780122